
Exponentiële groei
Inleiding
Groeiverschijnselen komen veel voor, denk aan het toenemen van geld dat je op de bank zet, het toenemen van de kosten als je meer km in de taxi zit, het groeien van de bevolking, enzovoorts.
Soms is er sprake van toename met een vaste hoeveelheid per tijdseenheid, soms is er sprake van toename die afhankelijk is van de hoeveelheid zelf: hoe groter de hoeveelheid, hoe groter ook de toename per tijdseenheid. Bij exponentiële groei is de toename een vast percentage van de totale hoeveelheid.
Je leert nu:
- werken met exponentiële groei en afname, bijpassende formules opstellen;
- groeifactoren omrekenen naar grotere tijdseenheden.
Je kunt al:
- werken met formules voor exponentiële groei en afname;
- werken met de begrippen macht, grondtal, exponent en groeifactor;
- werken met functies en grafieken.
Verkennen
Stel je voor dat je een heel groot vel papier hebt (A1). Het vel papier vouw je dubbel. Het dubbelgevouwen papier is dan 2 lagen dik. Vouw je dit papier nogmaals dubbel, dan is het papier 4 lagen dik.
Een echt vel papier kun je natuurlijk steeds moeilijker dubbelvouwen.
Wanneer je je het vel papier voorstelt als een onbegrensd vlak zonder dikte, kun je in principe blijven doorgaan met dubbelvouwen.
> Hoeveel lagen papier zijn er na 20 keer dubbelvouwen?
> Waarom zal dit met een A4tje nooit lukken?
Stel dat het onbegrensde vel papier 0,15 mm dik is.
> Hoe dik is het aantal lagen na 20 keer vouwen?
> Na hoeveel keer vouwen is het aantal lagen nog geen 10 cm dik?
> Van een ander vel papier is na net zo vaak vouwen het aantal lagen maar 5 cm dik. Hoe dik is dat papier?
Uitleg
Bacteriën planten zich voort door tweedeling. Elke bacterie brengt twee nieuwe bacteriën voort door zich te delen. Bij een geschikte constante temperatuur kan de groei van het aantal bacteriën als volgt verlopen:
| tijd in uren | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| aantal bacteriën | 600 | 1200 | 2400 | 4800 | 9600 | 19200 | 38400 |
Het aantal bacteriën wordt elk uur twee keer zo groot. Dat zie je door opeenvolgende waarden in de tabel op elkaar te delen:
`1200/600 = `2400/1200 = 4800/2400 = 9600/4800 = 19200/9600 = 2`
Je moet dus steeds met factor 2 vermenigvuldigen om het volgende aantal te vinden:
- op tijdstip 0 zijn er 600 bacteriën;
- na 1 uur zijn er 600 · 2 bacteriën;
- na 2 uur zijn er 600 · 2 · 2 bacteriën;
- na 3 uur zijn er 600 · 2 · 2 · 2 = 600 · 23 bacteriën;
enzovoort. Het aantal bacteriën groeit exponentieel met groeifactor 2 per uur.
Voor het aantal bacteriën B na t uur geldt in dit geval de formule B(t) = 600 · 2t.
Je ziet dat er machten worden gebruikt voor het herhaaldelijk vermenigvuldigen. In dit geval zijn het machten met grondtal 2, dit getal is de groeifactor per uur. Omdat de variabele t in de exponent zit, spreek je van exponentiële groei.
‡
Opgaven
-
Bekijk het verhaal van de bacteriegroei in de Uitleg.
-
Wat versta je onder de 'groeifactor' per uur van het aantal bacteriën?
-
Hoeveel procent bacteriën komt er elk uur bij?
-
Hoeveel bacteriën heb je na 12 uur? En hoeveel heb je er een uur later?
-
Hoeveel bacteriën heb je 3 uur later dan 12 uur na `t=0`?
-
De formule voor de bacteriegroei in de Uitleg is `B = 600 * 2^t`
-
Breng deze formule in beeld op je grafische rekenmachine. Zorg er voor dat er minstens 24 uur bacteriegroei in beeld komt.
-
Hoeveel bacteriën zijn er na 20 uur?
-
Op welk tijdstip zijn er meer dan 60000 bacteriën?
-
Op welk tijdstip is het aantal bacteriën dan weer verdubbeld (dus 120000 geworden)? Leg uit hoe je dat hebt berekend.
Theorie
Bij exponentiële groei moet je per tijdseenheid steeds met hetzelfde vermenigvuldigen.
Dit getal g heet de groeifactor die bij die tijdseenheid hoort: g > 0.
Om vast te stellen of een hoeveelheid H exponentieel groeit, deel je opeenvolgende waarden op elkaar. Komt daar steeds hetzelfde uit, dan heb je exponentiële groei. De hoeveelheid H groeit dan zo:
- Op t = 0 heb je de beginwaarde b.
- Op t = 1 heb je H = b · g.
- Op t = 2 heb je H = b · g · g = b · g2.
- Op t = 3 heb je H = b · g · g · g = b · g3.
Dus er geldt een formule van de vorm H = b · gt.
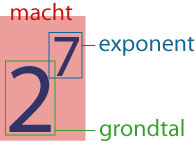
Bij exponentiële groei werk je met machten: vermenigvuldig je t keer hetzelfde getal g, dan schrijf je dat als gt. Dit is een macht, de groeifactor g heet het grondtal, t heet de exponent.
 Een voorbeeld van exponentiële groei is toename of afname met een vast percentage.
Bij een groei met p procent hoort de groeifactor: g = 1 + .
Een voorbeeld van exponentiële groei is toename of afname met een vast percentage.
Bij een groei met p procent hoort de groeifactor: g = 1 + .
Voor p > 0 neemt de hoeveelheid toe en is g > 1: exponentiële toename.
Voor p < 0 neemt de hoeveelheid af en is g < 1 (maar groter dan 0): exponentiële afname.
‡
Voorbeeld 1
Het aantal inwoners van D groeit volgens de formule N = 67000 · 1,024t.
Hierin is t de tijd in jaren en N het aantal inwoners van D (afgerond op duizendtallen).
t = 0 in het jaar 2000.
Met hoeveel procent per jaar groeit het aantal inwoners van D volgens deze formule?
In welk jaar heeft D meer dan 100.000 inwoners als deze groei zo doorgaat?
Antwoord
Er is sprake van exponentiële groei met een groeifactor van 1,024.
Elk jaar wordt het inwoneraantal met 1,024 vermenigvuldigd, dus 100% is een jaar later 102,4%.
Er komt jaarlijks 2,4% bij.
Als je deze formule invoert invoert in de rekenmachine heb je snel een tabel. En dan kun je aflezen voor welke waarde van t je voor het eerst boven de 100.000 zit. Je vindt t = 17.
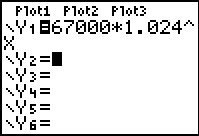
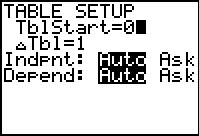
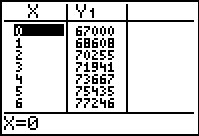
‡
Voorbeeld 2
Een krant zag in een reeks van jaren het aantal jaarabonnementen dalen.
| jaartal | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| aantal abonnementen (×1000) | 970 | 941 | 913 | 885 | 859 | 833 |
Stel op grond van deze tabel een zo goed mogelijk passende formule op die het verloop van het aantal duizenden abonnementen A als functie van de tijd t in jaren beschrijft. Neem voor 2000 t = 0.
Als het aantal jaarabonnementen onder de 500.000 zakt raakt de krant in problemen. In welk jaar is dat et geval als dit verloop niet wijzigt?
Antwoord
De jaartallen nemen gelijkmatig toe. Deling van opeenvolgende aantallen abonnementen levert steeds (ongeveer) 0,97 op, dus de daling
is een vorm van exponentiële groei. De groeifactor g ≈ 0,97 < 1, dus
er is sprake van exponentiële afname.
Het aantal abonnementen neemt jaarlijks met 3 procent af.
Een passende formule is daarom: A(t) = 970 · 0,97t.
Maak vervolgens een tabel van deze functie met de rekenmachine.
Ga na dat op t = 22 de waarde van A minder dan 500 is.
Op deze manier raakt de krant in 2022 in de problemen.
‡
Voorbeeld 3
Op 1 januari 2000 stond een bedrag van € 3500,00 op een spaarrekening.
De bank gaf op deze rekening een rente van 4% per jaar.
Neem aan dat dit alles vanaf 1-1-2000 niet verandert en stel een formule op voor het saldo S op deze rekening afhankelijk van de tijd t in jaren vanaf 1-1-2000. Maak een tabel die laat zien hoe het saldo zich ontwikkelde.
Antwoord

Bij een procentuele toename van 4% per jaar hoort een groeifactor van 1,04.
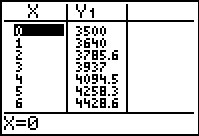
Op t = 0 is het saldo 3500 euro.
Op t = 1 is het saldo 3500 · 1,04 = 3640 euro.
Op t = 2 is het saldo 3500 · 1,04 · 1,04 = 3500 · 1,042 = 3785,60 euro.
Enzovoorts...
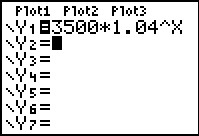
Een passende formule is daarom S = 3500 · 1,04t.
Als je deze formule invoert invoert in de rekenmachine heb je snel een tabel.
‡
Opgaven
-
In Voorbeeld 1 zie je hoe het aantal inwoners van D exponentieel groeit.
Het aantal inwoners van A groeit volgens de formule `N = 110000 * 1,013^t` met `t` in jaren vanaf 2000.
-
Waaraan zie je dat A een grotere stad is dan D?
-
Waaraan zie je dat het aantal mensen in A langzamer groeit dan D?
-
Met welke groeifactor neemt het aantal mensen in A jaarlijks toe? Wat is het jaarlijkse groeipercentage?
-
Maak nu de grafieken van de groeiformules van de steden D en A in één figuur op je grafische rekenmachine. Zorg er voor dat het snijpunt van beide grafieken in beeld komt.
-
Bepaal met je grafische rekenmachine het jaar waarin D groter wordt dan A als hun groei precies zo zal doorgaan. Hoeveel inwoners heeft D aan het einde van dat jaar?
-
Bekijk de tabel in Voorbeeld 2, waarbij sprake is van exponentiële afname.
-
Controleer dat de groeifactor per jaar inderdaad telkens ongeveer 0,97 is.
-
Welke formule vind je voor het aantal abonnementen `A(t)` als je `t=0` neemt in 2007?
-
Laat zien dat de krant in 2022 inderdaad in de problemen raakt.
-
Iemand zet op 1-1-2000 op een bankrekening € 800,- tegen 6% rente. De rente wordt jaarlijks op de bankrekening bijgeschreven. Er wordt verder geen geld op de bankrekening gestort of geld van de bankrekening gehaald.
Bekijk eventueel Voorbeeld 3.
-
Wat is de groeifactor per jaar van het tegoed op de bankrekening?
-
Hoeveel staat er op de bankrekening op 1-1-2005? Laat zien hoe je dat berekent.
-
Welke formule geldt voor het spaartegoed `S(t)`, waarin `t` de tijd in jaren na 1-1-2000 is?
-
Bereken het tegoed op 1-1-2020.
-
Neem de tabel over en vul in:
| procentuele toename per jaar |
13 |
–6 |
0,3 |
|
|
|
|
| groeifactor per jaar |
|
|
|
1,15 |
0,98 |
3,95 |
0,01 |
-
Van twee vogelsoorten die alleen op één bepaald eiland voorkomen neemt het
aantal de laatste jaren af. Tellingen leverden dit resultaat op:
| jaartal | 2004 | 2005 | 2006 | 2007 | 2008 |
| aantal vogels soort A | 5200 | 4888 | 4594 | 4319 | 4060 |
| aantal vogels soort B | 6400 | 6205 | 5998 | 5801 | 5598 |
- Leg uit dat het aantal vogels van soort A exponentieel afneemt. Hoeveel bedraagt de groeifactor per jaar?
- Hoeveel vogels van soort A zullen er in 2011 zijn als de afname zo door gaat?
- Het aantal vogels van soort B neemt ongeveer lineair af. Laat dat zien.
- In welk jaar zullen er van beide soorten vogels op zeker moment evenveel zijn als de groei zo door gaat?
Verwerken
-
De oppervlakte die door een snelgroeiende waterplant wordt bedekt neemt elke dag met 50% toe.
-
Met welk getal moet je de oppervlakte vermenigvuldigen als je de oppervlakte wilt weten die de waterplant morgen zal bedekken?
-
Neemt de oppervlakte van de waterplant in twee dagen met 100%toe? Of met een ander percentage? Leg uit.
-
Is hier sprake van exponentiële groei? Leg uit.
-
Iemand koopt aandelen ter waarde van 4000 euro. De aandelen nemen gedurende de eerste vier jaar elk jaar 11% in waarde toe.
-
Bereken de waarde van de aandelen na één jaar en na twee jaar.
-
Hoeveel bedraagt de groeifactor van de waarde van de aandelen?
-
Hoe kun je met behulp van de waarde na twee jaar de waarde na drie jaar berekenen?
-
De waarde na vier jaar is € 6072,28. Hoe kun je hieruit met behulp van de groeifactor de waarde na drie jaar berekenen?
-
In het zesde jaar stijgt de waarde van de aandelen van € 6740,23 naar € 7279,45. Met hoeveel procent is de waarde van de aandelen in het zesde jaar toegenomen? Wat is nu de groeifactor?
-
In het jaar 2000 zijn er in een natuurgebied 5000 herten. Uit tellingen is gebleken
dat dit aantal met 4% per jaar daalt.
-
Stel een formule op voor de 'groei' van het aantal herten vanaf het jaar 2000.
-
Bereken het aantal herten in het jaar 2010.
-
In welk jaar is het aantal herten voor het eerst gehalveerd?
-
Een kapitaal van € 10000,- wordt gedurende 10 jaar belegd in aandelen.
In de tabel zie je de groei van het kapitaal in de eerste 6 jaar.
| tijd in jaren |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| kapitaal in euro |
10415 |
10850 |
11295 |
11760 |
12250 |
12750 |
13280 |
Onder rendement wordt hier verstaan de procentuele toename van het belegde kapitaal per jaar.
-
Maak duidelijk dat het kapitaal in de eerste 6 jaar bij benadering exponentieel toeneemt.
-
Bereken voor deze periode het rendement (per jaar).
-
Maak een tabel van een kapitaal van € 10000,- dat 10 jaar wordt belegd bij een rendement van 8% per jaar.
-
Na hoeveel jaar is dit kapitaal verdubbeld?
-
Iemand belegt een kapitaal van € 10000,- gedurende 10 jaar.
Stel dat hij de eerste 5 jaar een rendement van 14% per jaar behaalt en de daarop volgende 5 jaar 4% per jaar.
Bereken het kapitaal `K` na 5 jaar en na 10 jaar.
-
Laat met een berekening zien of het de belegger meer oplevert in vergelijking met de vorige situatie als het rendement de eerste 5 jaar 4% is en de volgende 5 jaar 14%.
-
Twee scholen hebben te maken met teruglopende leerlingenaantallen:
| jaar (teldatum 1 sep.) | 2005 | 2006 | 2007 | 2008 | 2009 |
| aantal leerlingen school 1 | 1050 | 998 | 948 | 900 | 855 |
| aantal leerlingen school 2 | 1050 | 1005 | 960 | 915 | 870 |
- Bij één van beide scholen neemt het leerlingenaantal jaarlijks met een vast percentage af. Bij welke school is dat en met welk percentage?
- Hoe verloopt de afname van het leerlingenaantal van de andere school?
- School 2 lijkt uiteindelijk meer leerlingen over te houden dan school 1. Is dat ook zo? Licht je antwoord toe.
- In deze situatie heeft het geen zin om naar kleinere tijdseenheden dan een jaar te kijken. Waarom niet?
Testen
-
In de tabel hieronder zie je de grootte van een spaartegoed op 1 januari in een aantal opeenvolgende jaren.
| jaar | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| tegoed in € | 1000,00 | 1040,00 | 1081,60 | 1124,86 | 1169,86 | 1216,65 |
-
Bereken het verschil tussen de bedragen in 2005 en 2006. Hoe zou de tabel eruit zien als de groei na 2006 zich lineair zou voortzetten?
-
Je kunt uit a concluderen dat de groei van het spaartegoed niet lineair is. Ga na dat het tegoed exponentieel groeit.
-
Hoeveel bedraagt de groeifactor? En het groeipercentage?
-
Hoe groot zal het tegoed zijn op 1 januari 2020?
-
Iemand betaalt op 1 januari 2002 een huur van € 300,- (per maand). Er wordt een jaarlijkse huurverhoging verwacht van 5,5%.
-
Is hier sprake van exponentiële groei?
-
Bereken de huur op 1 januari 2003 en op 1 januari 2004.
-
Met hoeveel procent stijgt de huur per twee jaar toe?
-
Iemand koopt voor € 5000,- aandelen. In de volgende jaren blijkt dat de
aandelen elk jaar 12% in waarde dalen.
-
Stel een formule op voor de waarde van de aandelen `W(t)`, waarin `t` de tijd in jaren sinds de aankoop van de aandelen is.
-
Na hoeveel jaar is de waarde van de aandelen minder dan € 1000,= geworden?



 Een voorbeeld van exponentiële groei is toename of afname met een vast percentage.
Bij een groei met p procent hoort de groeifactor: g = 1 + .
Een voorbeeld van exponentiële groei is toename of afname met een vast percentage.
Bij een groei met p procent hoort de groeifactor: g = 1 + .





