
Lineaire vergelijkingen en ongelijkheden
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Uitleg
Opgaven
-
Bekijk in de Uitleg hoe het oplossen van een ongelijkheid in zijn werk gaat.
Je werkt in drie stappen:
-
Los eerst de vergelijking `30 + 25a = 18 + 27,5a` op.
Doe dit zelf nog eens algebraïsch zonder naar de uitleg te kijken.
-
Maak vervolgens de grafieken van `K_text(A)` en `K_text(B)` op de grafische rekenmachine.
Kies geschikte vensterinstellingen.
-
Lees de oplossing van de ongelijkheid uit de grafieken af.
-
Los de ongelijkheid `600 - 0,5x <= 400 + 1,5x` op.
Werk op dezelfde manier als in de voorgaande opgave en de uitleg.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
Twee cilindervormige kaarsen branden gelijkmatig op: de lengte `L` (in cm) van elke kaars is een lineaire functie van de brandtijd `t` (in uren). Op `t=0` worden beide kaarsen aangestoken. Kaars I heeft op dat moment een lengte van 30 cm en brandt met 1,5 cm per uur op. Kaars II heeft dan een lengte van 22 cm en brandt met 0,5 cm per uur op.
-
Stel voor elk van deze kaarsen een formule op voor `L` als functie van `t`.
-
Breng de bijpassende grafieken in beeld met je grafische rekenmachine.
-
Bepaal met de grafische rekenmachine vanaf welk tijdstip kaars II langer is dan kaars I.
-
In Voorbeeld 1 zie je hoe je deze ongelijkheid algebraïsch kunt oplossen.
Voer die algebraïsche oplossing stap voor stap uit.
-
In Voorbeeld 2 wordt de ongelijkheid `y_1 >= y_2` algebraïsch opgelost.
-
Los eerst de vergelijking `y_1 = y_2` algebraïsch op.
-
Leg uit hoe je de oplossing van de ongelijkheid uit de grafieken afleest.
-
In Voorbeeld 3 zie je hoe een lineaire ongelijkheid algebraïsch wordt opgelost.
Los zelf de volgende lineaire ongelijkheden op die manier op.
-
`25g - 150 < 18g + 60`
-
`0,8x + 15200 >= 2x + 8400`
-
`1/3 x - 25 > 16 + 1/2 x`
-
`(2g - 8)/4 + 4 >= 6`
Verwerken
-
Een leerlingenvereniging heeft een filmavond georganiseerd voor alle leerlingen
van de school. Voor de filmavond heeft de leerlingenvereniging € 400,=
uitgegeven. Om de gemaakte kosten te betalen, vragen ze € 2,50 voor een toegangskaartje.
Noem de gemaakte winst `W` en het aantal leerlingen dat komt kijken `l`.
-
Geef de formule voor `W` afhankelijk van `l`.
-
Hoeveel kaartjes moet de leerlingenvereniging verkopen om geen winst en geen verlies te draaien?
-
Hoeveel kaartjes zijn er verkocht als de winst groter is dan € 1000,=?
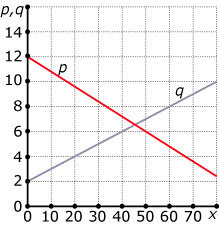 Bekijk de figuur. Los op: `p < q`.
Bekijk de figuur. Los op: `p < q`.
-
Twee personen willen vanaf het station naar huis gebracht worden met de taxi.
Ze hebben de keuze tussen de treintaxi en de gewone taxi. De treintaxi kost
€ 3,= per persoon, de gewone taxi rekent € 2,25 per rit en € 0,75 per gereden minuut.
-
Geef een formule voor de kosten van een gewone taxi, afhankelijk van het aantal minuten `m` dat de rit duurt.
-
Bepaal bij welk aantal minuten het voordeliger wordt om een treintaxi te nemen.
-
De taxi's rijden door de stad gemiddeld 60 kilometer per uur. De twee personen wonen zes kilometer van het station.
Welk type taxi raad je deze personen aan? Licht je antwoord toe met een berekening.
-
Los de volgende vergelijkingen en ongelijkheden algebraïsch op:
-
`55 - 6k = 4k - 25`
-
`12 - 4x >= 36 + 2x`
-
`25 - 1 2/3 t > 30 - 3t`
-
`1200 + 0,08a >= 1045 + 0,11a`
-
`(6 - 2x)/5 = (4 - x)/4`
-
`200 - (80 - x) = 4(x + 15)`
-
Een fabriek produceert een artikel dat voor € 10,= wordt verkocht. Het maken
van één exemplaar kost € 6,50 en de vaste kosten (voor het onderhoud van de
fabriek, de machines, de lonen enzovoort) zijn € 83000,=.
Ga er van uit dat elk geproduceerde exemplaar ook wordt verkocht.
-
Stel formules op voor de totale opbrengst `TO` en de totale kosten `TK` als functie van het geproduceerde aantal `q`.
-
De waarde van `q` waarbij opbrengst en kosten gelijk zijn heet het "break-even-point".
Bepaal met behulp van de grafische rekenmachine dit "break-even-point."
-
Bereken dit punt ook algebraïsch.
-
Bij welke waarden van `q` wordt er winst gemaakt?
-
Een aardewerkfabrikant verkoopt vazen voor € 5,= per stuk. Bij het maken van
de vazen rekent hij per dag aan vaste kosten € 1600,= en per vaas een bedrag
van € 3,=. Neem aan dat alle gemaakte vazen verkocht worden.
-
Geef de formule voor de kosten `K` in euro afhankelijk van het aantal geproduceerde vazen `v`.
-
Geef de formule van de opbrengst `O` in euro afhankelijk van het aantal verkochte vazen `v`.
-
Vanaf welk aantal verkochte vazen maakt de fabrikant winst? (Laat duidelijk zien welke methode je hierbij gebruikt!)
-
Bij welke dagproductie is de dagwinst € 2000,=?
Testen
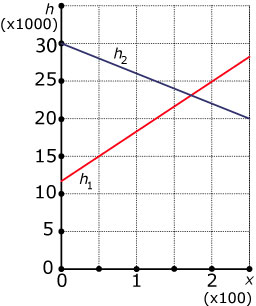 In deze figuur staan twee grafieken van lineaire functies `h_1` en `h_2`.
In deze figuur staan twee grafieken van lineaire functies `h_1` en `h_2`.
Los op: `h_1 <= h_2`.
-
Een autoverhuurbedrijf verhuurt een Toyota voor € 75,= per week. De benzinekosten
worden geschat op 9 cent per kilometer. Het bedrijf verhuurt ook een
Renault voor € 100,= per week. De benzinekosten van de Renault zijn ongeveer 6,5 cent per kilometer.
-
Je huurt de Toyota voor een week en je hebt € 125,=. Hoeveel kilometer kun je dan rijden?
Beantwoord dezelfde vraag voor de Renault.
-
Geef formules voor de kosten per week van de Toyota en de Renault, afhankelijk van het aantal gereden kilometers.
-
Teken met de grafische rekenmachine de grafieken voor de kosten per week van de Toyota en de Renault.
Schrijf op welke vensterinstellingen je gebruikt.
-
Bereken zowel algebraïsch als met grafische rekenmachine vanaf welk aantal kilometers de Renault goedkoper is.
-
Een bedrijf produceert pennen. De productiekosten zijn een kwartje per pen, de
vaste kosten € 100,= per dag. De pennen worden verkocht voor € 1,50. Vanaf
welk aantal verkochte pennen per dag maakt het bedrijf winst?

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Inleiding
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Uitleg
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Lineaire verbanden > Lineaire vergelijkingen en ongelijkheden > Theorie
 Bekijk de figuur. Los op: `p < q`.
Bekijk de figuur. Los op: `p < q`. In deze figuur staan twee grafieken van lineaire functies `h_1` en `h_2`.
In deze figuur staan twee grafieken van lineaire functies `h_1` en `h_2`.