
Als je de gewichten van zo'n 1000 aselect gekozen vrouwen uit de leeftijdsgroep van 20-<30 jaar meet, krijg je ongeveer een klokvormige frequentieverdeling. Maar mag je nu zeggen dat er sprake is van een normale verdeling?
Er bestaat normaal waarschijnlijkheidspapier. Op dat papier wordt een cumulatief relatief frequentiepolygoon een rechte lijn als er van een normale verdeling sprake is. Met behulp van de vuistregels kun je vanaf dat papier dan het gemiddelde en de standaardafwijking aflezen.
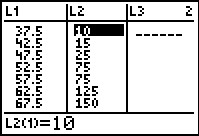
| gewicht | frequentie |
| 35-< 40 | 10 |
| 40-< 45 | 15 |
| 45-< 50 | 25 |
| 50-< 55 | 75 |
| 55-< 60 | 75 |
| 60-< 65 | 125 |
| 65-< 70 | 150 |
| 70-< 75 | 175 |
| 75-< 80 | 150 |
| 80-< 85 | 100 |
| 85-< 90 | 50 |
| 90-< 95 | 25 |
| 95-<100 | 15 |
| 100-<105 | 10 |
Bij een landelijk onderzoek zijn de gewichten bepaald van 1000 aselect gekozen volwassen vrouwen van 20-<30 jaar, zie tabel. De frequentieverdeling lijkt op die van een normale verdeling. Kun je nu zonder meer een normale verdeling als rekenmodel gebruiken voor deze groep vrouwen?
> Ga na of deze frequentieverdeling voldoet aan de vuistregels voor een normale verdeling.
> Is het voldoen aan de vuistregels voldoende reden om te concluderen dat een normale verdeling een bruikbaar rekenmodel is?``
Bij een landelijk onderzoek zijn de gewichten bepaald van 1000 aselect gekozen volwassen vrouwen van 20-<30 jaar, zie tabel. De frequentieverdeling lijkt op die van een normale verdeling met μ(L) = 70,125 en σ(L) ≈ 12,338. Kun je nu zonder meer een normale verdeling als rekenmodel gebruiken voor deze groep vrouwen?
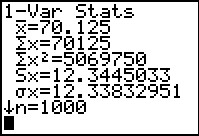
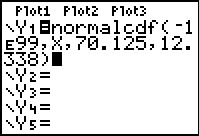
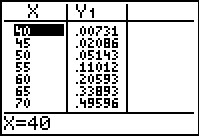
Zet je op normaal waarschijnlijkheidspapier kansen van de vorm P(L ≤ 40 | μ = 70,125 ∧ σ = 12,338) uit, dan krijg je een rechte lijn. Elke zuivere cumulatieve normale verdeling wordt op normaal waarschijnlijkheidspapier een rechte lijn.
Ga dit na met behulp van een blad normaal waarschijnlijkheidspapier. Dat kun je downloaden via
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Normaal of niet? > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Normaal of niet? > Theorie
Maak je van de gegeven frequentieverdeling een cumulatieve relatieve frequentieverdeling en zet je die uit op normaal waarschijnlijkheidspapier, dan zou je een rechte lijn moeten krijgen (je zet de cumulatieve relatieve frequenties uit tegen de rechter klassengrenzen). Bekijk via de website het resultaat. Merk op dat de cumulatieve relatieve frequentieverdeling en de normale verdeling goed overeenkomen! Kennelijk zijn deze gewichten ongeveer normaal verdeeld!``
‡
Zet je bij een normaal verdeelde variabele X met verwachting μ(X) en standaardafwijking σ(X) op normaal waarschijnlijkheidspapier kansen van de vorm P(X ≤ g) uit tegen g, dan krijg je een rechte lijn: elke zuivere cumulatieve normale verdeling wordt op normaal waarschijnlijkheidspapier een rechte lijn.
Maak je van een gegeven frequentieverdeling een cumulatieve relatieve frequentieverdeling en zet je die uit op normaal waarschijnlijkheidspapier, dan zou je een rechte lijn moeten krijgen als de frequenties normaal zijn verdeeld. De cumulatieve relatieve frequenties moeten daarbij tegen de bovengrenzen van de klassen worden uitgezet!
Op de website vind je bij de theorie een blad normaal waarschijnlijkheidspapier.
Vaak liggen op het normaal waarschijnlijkheidspapier de punten van de cumulatieve relatieve frequentieverdeling niet precies op een rechte lijn. Dan trek je een rechte lijn die zo goed mogelijk bij de getekende punten past. Je benadert dan je frequentieverdeling door de normale verdeling die bij die lijn hoort.
De verwachtingswaarde schat je vervolgens door af te lezen welk getal er bij 50% hoort.
En omdat één van de twee vuistregels zegt dat bij een normale verdeling 68% in het interval [μ – σ,μ + σ] ligt, is bij 84% de waarde van μ + σ af te lezen.
‡

De tabel geeft de diameters (in mm) van machinaal geproduceerde moeren. Ga na, dat deze diameters normaal zijn verdeeld en bereken het gemiddelde en de standaardafwijking.
| diameter | percentage |
| 12,8-< 12,9 | 0,1 |
| 12,9-< 13,0 | 2,1 |
| 13,0-< 13,1 | 13,6 |
| 13,1-< 13,2 | 34,1 |
| 13,2-< 13,3 | 34,0 |
| 13,3-< 13,4 | 13,6 |
| 13,4-< 13,5 | 2,0 |
| 13,5-< 13,6 | 0,1 |
Met de GR vind je μ(M) ≈ 13,20 en σ(M) ≈ 0,10 waarin M de diameter van een moer voorstelt.
Op nomaal waarschijnlijkheidspapier verschillen de cumulatieve relatieve frequentieverdeling vanuit de tabel en die gemaakt vanuit een normale verdeling met μ = 13,20 en σ = 0,10 vrijwel niet van elkaar. (Maak beide op een blad normaal waarschijnlijkheidspapier.)
Conclusie: M is normaal verdeeld met μ(M) ≈ 13,20 en
σ(M) ≈ 0,10.
‡
De lengteverdeling van Nederlandse mannen boven 20 jaar is bij benadering klokvormig. Via
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Normaal of niet? > Voorbeeld 2
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Normaal of niet? > Voorbeeld 2
zie je op normaal waarschijnlijkheidspapier hoe deze verdeling wordt benaderd door een rechte lijn.
Bepaal vanuit deze figuur het gemiddelde en de standaardafwijking van X.
Op deze lengteverdeling van Nederlandse mannen boven 20 jaar zijn de lengtes bij 50% en 84% af te lezen:
Je vindt een gemiddelde van ongeveer 181 cm met een standaardafwijking van 189 – 181 = 8 cm.
‡
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen
| bloeddruk | mannen | vrouwen |
| 105 | 2 | 1 |
| 110 | 4 | 3 |
| 115 | 6 | 5 |
| 120 | 16 | 15 |
| 125 | 15 | 12 |
| 130 | 6 | 6 |
| 135 | 7 | 7 |
| 140 | 7 | 7 |
| 145 | 7 | 8 |
| 150 | 2 | 5 |
| 155 | 1 | 3 |
| 160 | 1 | 2 |
| 165 | 15 | 1 |
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen