Normaalkromme

Antwoorden bij de opgaven

1. 1. `3,4 + 11,6 + 23,8 = 38,8`%.
   2. De staven beslaan ongeveer een even groot gebied als het gebied onder de kromme lijn tussen `L = 165` en `L = 180`.
   3. `8,4 + 2,2 + 0,5 = 11,1`%.
   4. Kleur het gebied onder de nromaalkromme vanaf `L = 190`.
   5. 100%
2. 1. `0,1 + 0,7 + 3,4 + 11,6 + 23,8 + 0,2 * 28,9 ~~ 45,4`%.
   2. 50% want het gemiddelde moet (als de figuur echt netjes symmetrisch is) de verdeling in twee gelijke delen verdelen.
   3. `8,4 + 2,2 + 0,5 = 11,1`%.
   4. `23,8 + 28,9 + 0,4 * 20,4 ~~ 60,9`%.
   5. Ook ongeveer 60,9%.
3. 1. `179,5 - < 180,5` en daar zit 5,5% van de soldaten in.
   2. `0,013 + 0,017 + 0,021 + 0,025 + 0,030 + 0,035 = 0,141` dus 14,1%.
   3. Dat zou ongeveer 68% moeten zijn.
   4. Ongeveer 6,6%.
   5. `0,022 + 0,027 + 0,034 + 0,040 + 0,047 + 0,053 = 0,223` dus 22,3%.
   6. Dat moet weer ongeveer 68% zijn.
   7. Het betreft de eerste vuistregel.
4. 1. -
   2. `17,8 + 12,2 = 30,0`%.
   3. `20,7 + 14,1 = 34,8`%.
   4. Redelijk, het is geen perfecte normale verdeling.
5. 1. -
   2. -
   3. 95 %.
   4. Redelijk, het is geen perfecte normale verdeling.
   5. 
   6. Bijna 100%.
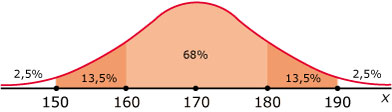
6. 1. I 2,5%, II 13,5%, III 34%, IV 34%, V 13,5%, VI 2,5%.
   2. 16%
   3. 81,5%
   4. 84%
7. 1. -
   2. 68% + 16% = 84%
   3. 68% + 13,5% = 81,5%
   4. 84%
8. 1. Normaal verdeeld.
   2. Normaal verdeeld.
   3. Waarschijnlijk niet normaal verdeeld, het gewicht is sterk te beïnvloeden door (slechte) eetgewoontes.
   4. Normaal verdeeld, wellicht afhankelijk van de manier waarop die reactietijd wordt getest.
   5. Niet normaal verdeeld, er zijn veel meer lagere inkomens dan top inkomens, de verdeling is erg scheef.
   6. Niet normaal verdeeld, kleinere wachttijden zullen vaker voorkomen dan grotere.
9. 1. Er ontstaat geen heel mooie symmetrische klokvorm, maar vooruit...
   2. `mu ~~ 1005` en `sigma ~~ 2,4` gram.
   3. Volgens het histogram 6%.
   4. 1000 gram is ongeveer het gemiddelde min 2 keer de standaardafwijking. Daar zou 2,5% onder moeten zitten volgens de vuistregels.
   5. Ongeveer 16%.
   6. Ongeveer 68%.
10. 1. 50%
    2. 85%
    3. `sigma_B = 50` en `mu_B = 1150` (uur).
    4. Omdat de verdeling breder is en het gebied in beide gevallen 100% voorstelt, moet de hoogte minder zijn.
    5. 95%
    6. 2,5%
11. 1. -
    2. 68%
    3. 2,5%
    4. 97,5%
    5. 2,5%
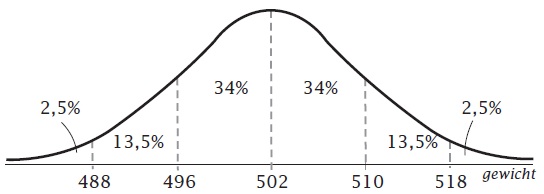
12. 1. `mu = 3,0` en `sigma = 0,2`
       `mu = 82` en `sigma = 6`.
    2. Bovenste normaalkromme: gebied is 16%.
       Onderste normaalkromme: gebied is 84%.
13. 1. 
    2. 32%
    3. 84%
    4. Nee, de vuistregels zijn hierbij niet te gebruiken.
    5. Ongeveer 16% + 20% = 36%.
    6. Ja, waarschijnlijk hebben ze gelijk.
14. 1. 68%
    2. 16%
    3. 84%
    4. Onder een IQ van 85.
15. 1. Tussen 32 en 64.
    2. Tussen 32 en 80.
    3. 16%
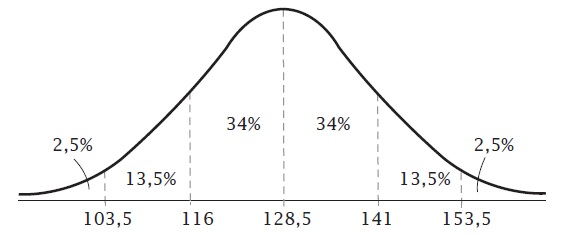
16. 1. `mu = 162` cm en `sigma = 6,5` cm.
    2. -
    3. `a = 13`
    4. 168,5 cm.
17. 1. 
    2. 84%
    3. 5%
    4. Nee, de vuistregels zijn hierbij niet te gebruiken.