Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek > Totaalbeeld > Samenvatten


Je hebt nu het onderwerp Statistiek doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:
  1. kwalitatieve variabelen — discrete/continue kwantitatieve variabelen
  2. (relatieve) frequentie — frequentietabel, frequentieverdeling — somfrequenties — klassenindeling
  3. staafdiagram, lijndiagram, cirkeldiagram — histogram, (som)frequentiepolygoon — steelblad diagram
  4. centrummaten: modus, mediaan, gemiddelde — spreidingsmaten: spreidingsbreedte, kwartielafstand, standaardafwijking — kwartielen, boxplot
  5. klokvormige frequentieverdeling — twee vuistregels
Activiteitenlijst:
  1. representativiteit van een steekproef bedoordelen — soorten statistische variabelen herkennen
  2. (som)frequentieverdelingen maken — werken met klassen
  3. diagrammen gebruiken om statistische resultaten weer te geven (ook met de GR en/of Excel)
  4. centrummaten en spreidingsmaten berekenen (schatten) zowel met als zonder klassenindeling (ook met de GR en/of Excel)
  5. uitspraken doen op grond van steekproefverdelingen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek > Totaalbeeld > Achtergronden

Testen

Opgaven

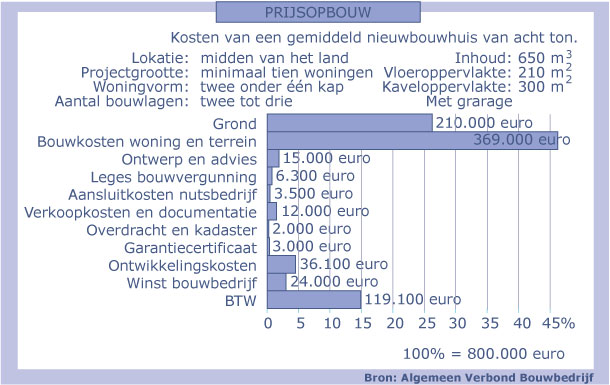
  1. In de figuur (uit september 2000) wordt aangegeven hoe de prijs van een nieuwbouwhuis is opgebouwd.



    1. Hoeveel is de grondprijs per vierkante meter bij deze woningen?
    2. Bereken hoeveel procent van de totale kosten opgaan aan bouwkosten woning en terrein.
    3. Maak een cirkeldiagram van de prijsopbouw van deze woningen. Werk met vier categorieën, te weten: grond, bouwkosten, BTW en overige.
    4. Het hoge BTW-tarief is 19%. In de figuur zie je dat aan BTW ongeveer 15% moet worden betaald. Geef een verklaring voor dit verschil.

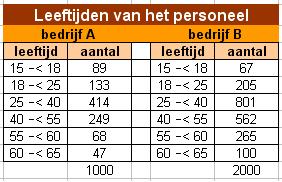  2. Deze tabel geeft de leeftijden van het personeel van twee bedrijven.
    1. Verwerk de aantallen werknemers van bedrijf A in een cirkeldiagram met straal 3 cm.
    2. Je wilt voor bedrijf B ook een cirkeldiagram maken. Hoe groot moet je de straal nu nemen?
    3. Teken een frequentiepolygoon bij de gegevens van bedrijf B.
    4. Beide bedrijven willen fuseren. Werknemers vanaf 60 jaar kunnen gebruik maken van een afvloeiingsregeling. Hoeveel procent van de werknemers van het gefuseerde bedrijf kunnen daarvan gebruik maken?

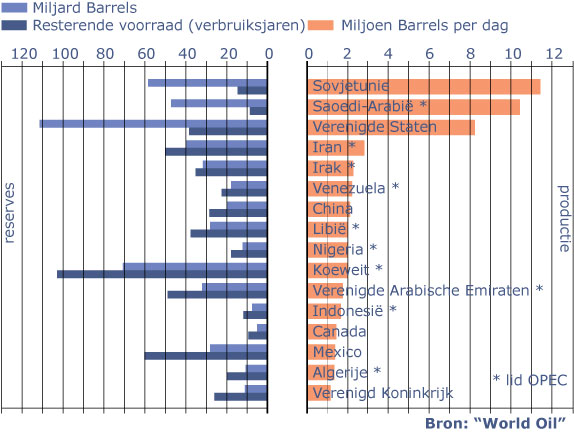
  3. In de figuur vind je gegevens over de oliereserves en de olieproductie uit "Aardolie, de halve wereld draait er op", van de Stichting School en Bedrijf.



    1. Welk land heeft de meeste reserves gerekend in barrels?
    2. Welk land heeft de meeste reserves gerekend in verbruiksjaren?
    3. Verklaar de verschillen tussen a en b.
    4. Hoeveel procent van de reserves is in handen van de OPEC-landen?
    5. En hoeveel procent van de productie is in handen van de OPEC-landen?
    6. Geef zowel de reserves (in miljarden barrels) als de productie (in miljoenen barrels per dag) weer in een cirkeldiagram. Neem als categorieën: de OPEC-landen, de Verenigde Staten, de voormalige Sovjet-Unie en overige.

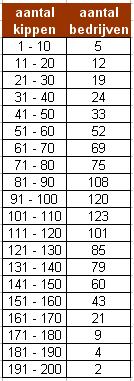  4. Uit onderzoek van het gemengde boerenbedrijf bleek het houden van kippen een belangrijke rol te spelen bij het tot stand komen van het inkomen van deze boeren. Daarom werd de boeren gevraagd het aantal kippen op hun bedrijf op te geven.
    1. Maak van deze gegevens een histogram. Hoeveel bedrijven deden mee?
    2. Welke klasse is de modale klasse?
    3. Teken een cumulatieve relatieve frequentiepolygoon.
    4. Schat de mediaan en de beide kwartielen. Teken een boxplot bij deze gegevens.
    5. Bereken het gemiddelde en de standaarddeviatie.
    6. Noem het aantal kippen per bedrijf `x`. Heeft `x` een klokvormige verdeling?
    7. Ga na of 68% van de bedrijven een hoeveelheid kippen heeft binnen het interval `[bar(x) - sigma_x, bar(x) + sigma_x]`.
    8. Ga er van uit dat het aantal kippen op een gemengd boerenbedrijf een klokvormige verdeling kent die wordt bepaald door het gemiddelde en de standaardafwijking berekend bij e. Hoeveel kippen hebben dan de 2,5% gemengde boerenbedrijven met de meeste kippen?

  5. Op de verpakking van een literpak melk staat: Inhoud 1 L. In werkelijkheid wil dat nog wel eens iets meer of minder zijn. Uit metingen blijkt een gemiddelde inhoud van 1,002 L. De standaardafwijking is 0,004 L. Ga er van uit dat de verdeling van de inhoud klokvormig is. Geef met behulp van de vuistregels bij de volgende uitspraken aan of ze waar of niet-waar zijn.
    1. Ongeveer 95% van de pakken melk heeft een inhoud van meer dan 1,010 L.
    2. Ongeveer 5% heeft een gewicht onder 0,994 L.
    3. Ongeveer 32% van de pakken melk bevat meer dan 0,998 en minder dan 1,006 L.
    4. Ongeveer 50% van de pakken melk bevat 1,002 L.
    5. Minimaal 90% van de pakken melk bevat meer dan 1 L.

  6. Je ziet hier gegevens over het voor komen van de ziekte AIDS uit 2000.



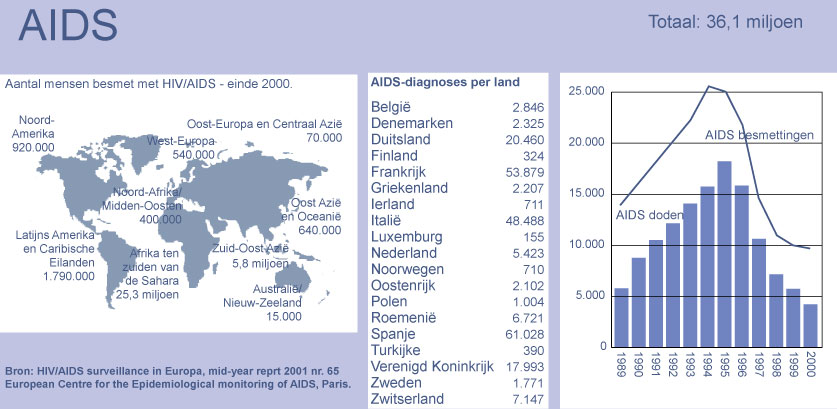
    1. In welk werelddeel is het aantal mensen dat met HIV/AIDS besmet is het grootst? Hoeveel mensen in dat werelddeel betreft het?
    2. In welk land in Europa is het aantal mensen dat met HIV/AIDS besmet is het grootst?
    3. Kun je op basis van deze gegevens concluderen dat de kans dat je iemand die met HIV/AIDS is besmet tegenkomt in Luxemburg het kleinst is?
    4. Welke gegevens heb je nodig om de aantal AIDS-diagnoses in de verschillende Europese landen te vergelijken?
    5. Maak een schatting van het aantal AIDS-doden in 1995.
    6. Maak een schatting van het totaal aantal AIDS-doden tussen 1 januari 1989 en 1 januari 1996.
    7. Op basis van deze gegevens kun je een cumulatief frequentiepolygoon tekenen waarin is aangegeven hoeveel mensen er sinds 1989 gestorven zijn aan AIDS. Doe dat.

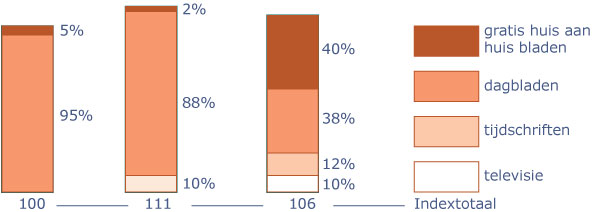
  7. Hier zie je waaraan een bedrijf in 2007, 2008 en 2009 de reclamegelden besteedde. In 2007 werd € 1.500.000,= voor reclame uitgegeven.



    1. Bereken hoeveel het bedrijf in 2008 aan reclame heeft uitgegeven. Bereken ook de reclameuitgaven in 2009.
    2. Mag je uit de gegevens concluderen dat
      • het bedrijf in 2008 11% meer uitgaf aan reclame dan in 2007?
      • het bedrijf in 2009 5% minder uitgaf aan reclame dan in 2008?
      Licht je antwoord toe.
    3. Bereken hoeveel het bedrijf over de drie jaar in totaal uitgaf voor reclame in huis aan huis bladen. Hoeveel is dat gemiddeld per jaar?
    4. Vergelijk de uitgaven aan reclame in dagbladen in 2007 met die in 2008. Met hoeveel procent zijn deze uitgaven veranderd?
    5. Welke van deze conclusies is waar?
      • In 2008 is meer aan reclame in dagbladen besteed dan in 2009 besteed is aan de totale reclame uitgezonderd de t.v.-reclame.
      • In 2009 is meer dan € 1.500.000,= uitgegeven aan reclame in drukvorm.

Toepassen

  1. Coopertest

    Bij de lessen lichamelijke opvoeding wordt op veel scholen de Coopertest gehouden. Meer informatie over deze test vind je via:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek > Totaalbeeld > Toepassingen

    In 2004 volbrachten 182 leerlingen in klas 4 en 5 een Coopertest. Van de leerlingen die de Coopertest (12 minutenloop) uitliepen is de afgelegde afstand genoteerd. Misschien kun je ook werken met gegevens van je eigen school!
    1. Welke klassenindeling zou je kiezen voor de vrouwen en welke voor de mannen om te kunnen concluderen of de conditie slecht, redelijk, goed of zeer goed is?
    2. Verwerk de gegevens voor vrouwen en mannen apart in twee afzonderlijke histogrammen.
    3. Verwerk de gegevens voor de vrouwen in een cirkeldiagram. Verwerk de gegevens voor de mannen in een cirkeldiagram.
    4. Welk percentage vrouwen heeft een goede of zeer goede conditie? Welk percentage mannen heeft een goede of zeer goede conditie?
    5. Typeer de afgelegde afstanden van de mannen en de vrouwen bij de Coopertest in gemiddelde, modus en mediaan.
    6. Teken van de resultaten van de mannen en van de vrouwen een boxplot. Bereken de kwartielafstand en de spreidingsbreedte.
    7. Doe een uitspraak op grond van beide boxplots waarin je de conditie van de mannen en de vrouwen met elkaar vergelijkt.
    8. Bereken voor beide groepen de standaardafwijking.
    9. Van hoeveel procent van de mannen en van hoeveel procent van de vrouwen wijkt de gelopen afstand meer dan de standaardafwijking van het gemiddelde af?
    10. Van hoeveel procent van de mannen en van hoeveel procent van de vrouwen wijkt de gelopen afstand meer dan twee keer de standaardafwijking van het gemiddelde af?
    11. Doe een uitspraak op grond van deze laatste gegevens bij waarin je de conditie van de mannen en de vrouwen met elkaar vergelijkt.

  2. Leeftijdsdiagrammen NL

    Je ziet hier vier leeftijdsdiagrammen van Nederland.



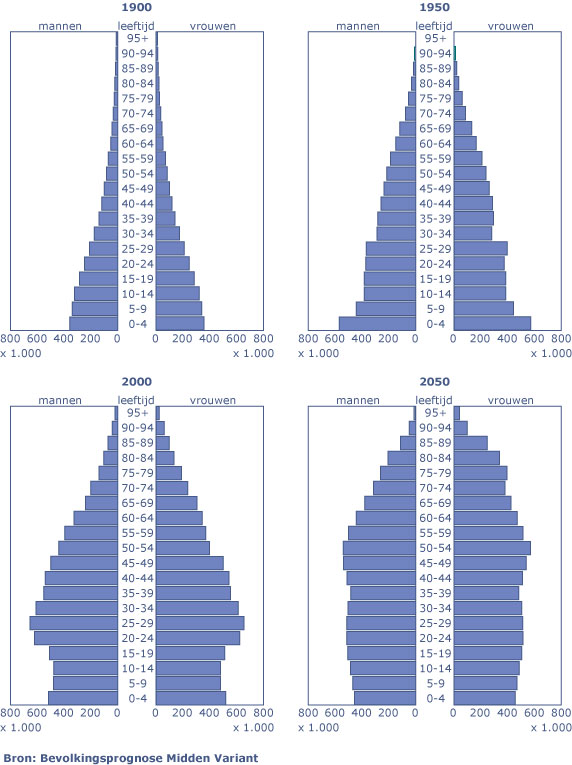
    1. Wat voor soort diagrammen zijn dit?
    2. Hoeveel kinderen van `0 - 4` waren er in 1900 ongeveer? En in 1950?
    3. In de jaren rond 1950 zijn er nogal veel kinderen geboren. Waaraan kun je dat zien?
    4. Waaraan kun je zien dat Nederland aan het "vergrijzen" is?
    5. Waaraan kun je zien dat vrouwen gemiddeld ouder worden dan mannen?
    6. De belangrijkste centrummaat bij een leeftijddiagram is de modale klasse. Welke klasse was in 1900 de modale klasse? En in 2050?
    7. Welke gevolgen heeft het feit dat de modale klasse steeds hoger komt te liggen?
    8. De bevolkingsopbouw van Nederland is ook goed zichtbaar te maken in boxplots. Teken bij het leeftijdsdiagram van 1900 een boxplot (mannen en vrouwen samen). Doe dat ook bij het geschatte leeftijdsdiagram van 2050. Noem minstens drie karakteristieke verschillen en geef er verklaringen bij.

Examenopgaven

  1. Oversteken

    Men heeft onderzoek gedaan naar de loopsnelheden van voetgangers. Bij dit onderzoek zijn de voetgangers in 3 leeftijdsgroepen verdeeld, namelijk kinderen, volwassenen en ouderen. Met de gegevens uit het onderzoek heeft men een boxplot gemaakt voor de loopsnelheden van de groep ouderen.



    De snelheden die bij de boxplot vermeld zijn, zijn in meters per seconde. Meer gedetailleerde informatie over de groepen zie je in de volgende figuur.



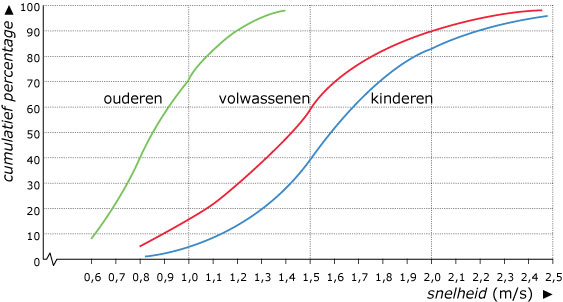
    Op de verticale as staat een cumulatief percentage; dit houdt in dat afgelezen kan worden hoeveel procent van de mensen van de verschillende groepen met de aangegeven snelheid of een lagere snelheid loopt. Zo kun je bijvoorbeeld aflezen dat voor de groep ouderen bij een snelheid van 1 m/s het cumulatieve percentage bijna 70 is. Dus bijna 70% van de ouderen loopt met een snelheid van 1 m/s of langzamer. Aan de hand van onder andere deze gegevens wordt een model gemaakt voor de tijd die de mensen nodig hebben om een weg over te steken.
    Neem aan dat de loopsnelheden ook voor het oversteken van een weg gelden. We bekijken het oversteken van een 20 meter brede weg. Er wordt recht overgestoken, dus men loopt daarbij 20 m.
    1. a) Maak met behulp van de gegevens uit het boxplot voor het oversteektijden van ouderen. Licht je werkwijze toe.
    Tot nu toe hebben we alleen gekeken naar de tijd van oversteken zelf. Als je bij een weg aankomt, kun je niet altijd meteen oversteken; soms moet je een aantal seconden wachten. Deze wachttijd hangt samen met de drukte op de weg en de benodigde oversteektijd. De drukte op de weg wordt aangegeven met het aantal voertuigen dat per uur passeert (voertuigenintensiteit). Omdat ouderen in het algemeen minder snel lopen, zal voor deze groep de benodigde oversteektijd en dus ook de wachttijd groter zijn dan bijvoorbeeld voor kinderen. Er is een model gemaakt voor de samenhang tussen oversteektijd, voertuigenintensiteit en verwachte wachttijd.



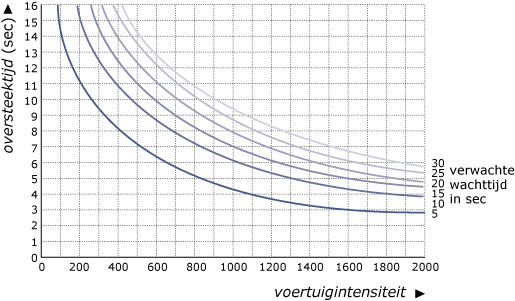
    In de figuur hierboven is dat voor zes verschillende wachttijden in beeld gebracht. Uit deze figuur is bijvoorbeeld af te lezen dat volgens dit model bij een oversteektijd van 9 s en een voertuigenintensiteit van 700 voertuigen per uur rekening gehouden moet worden met een wachttijd van 15 s.
    1. Teken de grafiek die het verband aangeeft tussen de oversteektijd en de verwachte wachttijd bij een voertuigenintensiteit van 800. Teken de grafiek alleen voor wachttijden van 5 tot en met 30 s.
    We willen een beeld krijgen van de totale tijd die een rol speelt bij het oversteken van een weg van 20 m breed en een voertuigenintensiteit van 800 voertuigen per uur. We spreken dan over de somtijd. Als we iemands verwachte wachttijd en zijn oversteektijd optellen, krijgen we zijn somtijd. We bekijken nu de groep van volwassenen. De hoogste snelheid die in deze groep is waargenomen is 2,6 m/s.
    1. Wat is de langste somtijd en wat is de kortste somtijd van de 10% snelste volwassenen? Licht je antwoord toe.

    (bron: examen wiskunde A havo 1994, tweede tijdvak)


  2. Vaders en zonen

    De Engelsman Karl Pearson was een van de grondleggers van de moderne statistiek. Hij heeft zich vaak bezig gehouden met statistiek over biologische onderwerpen. Ongeveer een eeuw geleden onderzocht hij, samen met zijn collega Alice Lee, of in Engeland zonen gemiddeld langer zijn dan hun vaders. Zij vergeleken de lengtes van 1064 zonen en hun vaders. De zonen studeerden allen aan een Londense universiteit.
    1. Is hier sprake van een aselecte steekproef? Licht je antwoord toe.
    Op de bijlage zie je een overzicht van de resultaten, zie

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek > Totaalbeeld > Toepassingen

    Elke stip stelt één vader-zoon-paar voor. De lengte van de vader staat op de horizontale as, de lengte van de zoon op de verticale as. De lengtes zijn gegeven in inches (1 inch = 2,54 cm).
    In de figuur is een lijn getekend. Als een stip op deze lijn ligt, dan zijn de vader en de zoon precies even lang. We noemen een vader en zijn zoon ongeveer even lang als ze minder dan 2 inch in lengte verschillen.
    1. Teken in de figuur op de bijlage het gebied waarin de punten liggen die horen bij vaders en zonen die ongeveer even lang zijn. Licht je werkwijze toe.
    2. Kun je met behulp van het getekende gebied concluderen dat de zonen gemiddeld langer zijn dan hun vaders? Licht je antwoord toe.
    Op de bijlage zie je een boxplot van de lengtes van de 1064 vaders. De vijf kenmerkende getallen van de boxplot staan erbij.
    Op de bijlage vind je ook een lijst met de lengtes van alle 1064 zonen. De getallen in deze lijst staan op volgorde van grootte. Na iedere 10 getallen staat een streepje. Na iedere 50 getallen staat bij het streepje hoeveel getallen er tot daar staan.
    1. Teken de boxplot van de lengtes van de zonen. Schrijf de vijf kenmerkende getallen van de boxplot erbij.
    Het onderzoek dat bovenstaande getallen opleverde, is ongeveer honderd jaar geleden gedaan. In die tijd hadden jonge mannen een gemiddelde lengte van 68,6 inch. Dat is niet zo groot want 68,6 inch is maar 174 cm (1 inch = 2,54 cm).
    Tegenwoordig is de helft van de jonge mannen langer dan 182 cm.
    Honderd jaar geleden was veel minder dan de helft van de jonge mannen zo lang. De lengte was toen klokvormig verdeeld met een gemiddelde van 68,6 inch en een standaardafwijking van 2,7 inch.
    1. Onderzoek met de vuistregels of het aantal jonge mannen langer dan 182 cm in die tijd groter of kleiner dan 16% van het totaal aantal jonge mannen was.

    (bron: examen wiskunde A havo 2003, eerste tijdvak, aangepast)