Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Kansen > Totaalbeeld > Samenvatten


Je hebt nu het onderwerp Kansen doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:
  1. kansexperiment — gebeurtenis — experimentele kans — relatieve frequentie — simulatie
  2. aselect — theoretische kans — wet van de grote aantallen
  3. vaasmodel — kansboom — trekking met/zonder teruglegging
  4. toevalsvariabele — kansverdeling — verwachtingswaarde
Activiteitenlijst:
  1. kansen bepalen op grond van kansexperimenten en/of simulaties
  2. kansen bepalen op grond van redeneringen met even waarschijnlijke mogelijkheden
  3. kansen berekenen m.b.v. kansbomen — het vaasmodel gebruiken
  4. een kansverdeling maken — de verwachtingswaarde berekenen — kansen berekenen waarin het gaat om minstens of hoogstens een bepaald aantal

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Kansen > Totaalbeeld > Achtergronden

Testen

Opgaven

  1. Vertaal de volgende situaties in een vaasmodel.
    1. Bij de presidentsverkiezingen in de Verenigde Staten in 2000 ging de verkiezingsstrijd tussen de presidentskandidaten Al Gore en George Bush. Gore had op zeker moment ongeveer 40% van de kiezers achter zich en Bush ook. De overige kiesgerechtigde Amerikanen zouden niet gaan stemmen. Je komt vier toeristen uit de Verenigde Staten tegen. Hoe groot is de kans dat ze alle vier op Gore zouden stemmen op dat moment?
    2. Bij een gevaarlijke reddingsoperatie moeten drie vrijwilligers een brandend gebouw in. Er zijn twee brandweercorpsen uitgerukt: corps A met 10 leden en corps B met 15 leden. Alle leden van de brandweercorpsen melden zich als vrijwilliger. De drie vrijwilligers worden door het lot aangewezen. Hoe groot is de kans dat ze alle drie bij corps A horen?
    3. Je gooit met drie gewone dobbelstenen. Wat is de kans op een som van 15 ogen?
    4. Je bent je pincode vergeten. Die pincode bestaat uit vier cijfers en alle mogelijkheden zijn toegestaan. Je wilt geld uit de giromaat halen. Je toetst zomaar een pincode in. Hoe groot is de kans dat het de juiste is?

  2. Iemand werpt met twee viervlaksdobbelstenen. Dergelijke dobbelstenen hebben de vorm van een regelmatig viervlak met daarop de getallen 1, 2, 3 en 4. Er wordt gelet op de som van de getallen die onder komen te liggen.
    1. Simuleer met behulp van toevalsgetallen 40 worpen met twee van die dobbelstenen. Hoe groot is de experimentele kans op 4?
    2. Hoe groot is de theoretische kans op 4?

  3. In een vaas zitten 20 balletjes, 10 rode, 5 witte en 5 blauwe. Uit die vaas worden aselect drie balletjes tegelijk gehaald.
    1. Maak een kansboom bij deze situatie.
    2. Hoe groot is de kans dat er 2 rode en 1 blauw balletje worden getrokken?
    3. Hoe groot is de kans op 1 balletje van elke kleur?
    4. Hoeveel rode balletjes verwacht je?

  4. Een gezin bestaat uit vier personen: vader Jan, moeder Jannie, kinderen Wim en Marietje. Twee van hen moeten de afwas doen. Wie dat zijn wordt bepaald door loting.
    1. Hoe groot is de kans dat beide kinderen de afwas moeten doen?
    2. Hoe groot is de kans dat beide mannelijke gezinsleden moeten afwassen?

  5. Het bekende dominospel bestaat uit 28 stenen. Elke steen bestaat uit twee helften. Op elke helft komen 0, 1, 2, 3, 4, 5, of 6 ogen voor. Je kiest aselect één steen.
    1. Laat zien waarom er 28 dominostenen zijn.
    2. Hoe groot is de kans dat het een "dubbele" is (aan beide kanten evenveel ogen)?
    3. Hoe groot is de kans dat de som van het aantal ogen minstens 10 is?
    4. Hoe groot is de kans dat het verschil van het aantal ogen hoogstens 2 is?
    5. Hoe groot is de kans dat het grootste aantal ogen op één van beide zijden 3 is?
    6. Je speelt met Petra een spelletje domino. De hiernaast getekende stenen heb jij bij het delen gekregen. Jij begint het spel met de "dubbel-vijf". Hoe groot is de kans dat zij kan aanleggen?

  6. Er worden voor Sinterklaas in een gezin van vier personen lootjes getrokken. Als iemand zijn eigen naam trekt moet er opnieuw worden geloot.
    Hoe groot is de kans dat dit het geval is?

  7. Als je twee opeenvolgende verkiezingen voor de Tweede Kamer met elkaar vergelijkt, dan zie je dat mensen regelmatig van partij veranderen. Aan 415 Nederlanders die beide keren hebben gestemd is gevraagd op welke partij dat was. De gegevens staan in deze tabel. De categorie "overige" wordt opgevat als één partij.



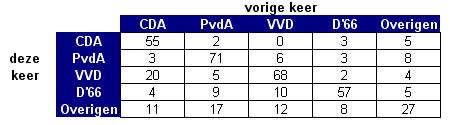
    Bereken in vier decimalen nauwkeurig de kans dat een willekeurig gekozen ondervraagde
    1. de vorige keer op het CDA stemde;
    2. deze keer op de PvdA stemde;
    3. weer op zijn eigen partij stemde;
    4. die de vorige keer op de PvdA stemde nu op het CDA stemde;
    5. die de vorige keer op D'66 stemde nu op een andere partij stemde.

  8. Mantoux-test

    Ongeveer 0,02% van alle mensen lijdt aan TBC (tuberculose). Om te onderzoeken of iemand met TBC is besmet wordt er vlak onder de huid een stof ingebracht waarop 98% van de mensen die aan tbc lijden positief reageert. Echter ook ongeveer 1% van de mensen die niet aan TBC lijden reageert er positief op. Deze test heet de Mantoux-test.
    1. Maak van de gegevens een tabel. Ga uit van 1.000.000 mensen.
    2. Iemand ondergaat deze Mantoux-test en reageert positief. Hoe groot is de kans dat hij niet aan tbc lijdt?

Toepassen

  1. Chuck-a-luck

    Bekijk de regels van het spel "Chuck-a-luck" via

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Kansen > Totaalbeeld > Toepassingen

    1. Stel een bij dit spel passende kansverdeling op.
    2. Bereken de bijbehorende verwachtingswaarde.
    3. Wat adviseer je een casino dat dit spel wil invoeren?

  2. Sterftetabellen

    Verzekeringsmaatschappijen gebruiken veel kansrekening. Bij het afsluiten van een levensverzekering willen verzekeraars weten wat de kans is dat de verzekerde binnen een bepaalde tijd overlijdt. Daarbij wordt gebruik gemaakt van tabellen zoals je die kunt vinden via:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Kansen > Totaalbeeld > Toepassingen

    Deze tabellen zijn gebaseerd op statistisch onderzoek en worden van tijd tot tijd bijgesteld.
    1. Hoeveel procent van de mensen die de leeftijd van 25 jaar hebben bereikt, sterven voor hun dertigste?
    2. Hoeveel procent van de mensen die 60 jaar worden, sterven voor hun zeventigste?
    3. Gebruik nog eens de gegeven sterftetabel. Bereken in vier decimalen nauwkeurig de kans dat iemand die 50 jaar wordt, ook nog zijn zeventigste verjaardag zal halen.
    4. Bereken ook de kans dat iemand die 50 jaar wordt, binnen 20 jaar zal sterven.
    5. Bereken de levensverwachting van een vijftigjarige man met behulp van deze tabel in Excel.
    Stel je een levensverzekering voor waarbij je het verzekerde bedrag in één keer krijgt uitbetaald wanneer je op de afgesproken datum nog in leven bent. Je betaalt de premie in één keer op het moment dat je de levensverzekering afsluit. Stel je voor dat je op 30-jarige leeftijd zo’n levensverzekering afsluit met als verzekerd bedrag € 100.000,00. Dit bedrag wordt uitgekeerd op het moment dat je 65 jaar wordt en nog in leven bent. De premie kan echter lager zijn dan € 100.000,00. Anders kun je immers beter zelf het geld op de bank zetten!
    1. Waarom is dat zo?
    2. Hoe hoog zou die premie moeten zijn op grond van de gegeven tabel? Licht je antwoord toe, houd rekening met overlevingskansen en rentestand.

Examenopgaven

  1. Helderziendheidstest

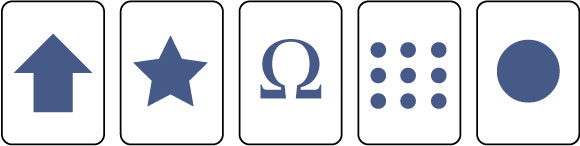
    Bij een helderziendheidstest wordt een stapel van 25 kaarten gebruikt, waarin elk van de onderstaande kaarten 5 keer voorkomt. De kaarten worden goed geschud en vervolgens worden er drie kaarten tegelijk uit de stapel getrokken. De proefpersonen moeten voorspellen welke kaarten getrokken zullen worden.
    Een proefpersoon raadt op goed geluk dat er 2 sterren en 1 cirkel worden getrokken.
    Bereken de kans dat zijn "voorspelling" uitkomt.



    (bron: examen wiskunde A havo 1989, tweede tijdvak)


  2. Hoe betrouwbaar is een keten?

    Bij een ingewikkeld apparaat is vaak een keten van onderdelen nodig om het geheel te laten functioneren. Daarbij is de betrouwbaarheid van een keten (zoals in onderstaande figuur) kleiner dan de betrouwbaarheid van de afzonderlijke delen. Dat komt doordat het uitvallen van één onderdeel het uitvallen van de gehele keten tot gevolg heeft. Bekijk een keten van 5 onderdelen (A, B, C, D, E), die elk een kans van 10% hebben om uit te vallen, oftewel elk een betrouwbaarheid hebben van 90%.


    1. Laat zien dat de betrouwbaarheid van deze keten ongeveer 60% is.
    Men kan de betrouwbaarheid vergroten door naast de keten van bovenstaande figuur nog zo’n keten te schakelen (zie de volgende figuur). Dit heeft het voordeel dat als één keten uitvalt het systeem toch blijft functioneren.


    1. Bereken de betrouwbaarheid van dit systeem.
    Een nog beter systeem krijgt men door de 10 onderdelen zo te schakelen als de volgende figuur aangeeft. Elk van de tien onderdelen heeft weer een betrouwbaarheid van 90%.


    1. Bereken de betrouwbaarheid van dit laatste systeem.

    (bron: examen wiskunde A havo 1991, eerste tijdvak)


  3. Linkshandigheid

    Bij de gezondheidsenquête van 1985, uitgevoerd door het Centraal Bureau voor de Statistiek, waren vragen opgenomen over linkshandigheid. Van linkshandige meisjes en jongens in de leeftijd van 10-20 jaar is nagegaan hoe het zit met de links- of rechtshandigheid van de ouders. Het resultaat hiervan staat in de tabel.

    CBS 1985 één van de ouders of beide ouders linkshandig beide ouders rechtshandig
    aantal meisjes linkshandig 32 72
    aantal jongens linkshandig 40 96

    Een linkshandige jongen en een linkshandig meisje (uit die leeftijdscategorie) beginnen een relatie. Na verloop van tijd maken de ouders van beide kinderen kennis met elkaar. Die ouders blijken alle vier rechtshandig te zijn.
    Hoe groot is de kans daarop?

    4. (bron: examen wiskunde A havo 1991, eerste tijdvak, gedeelte)