
De driehoek van Pascal
Inleiding
Sommige moderne steden hebben een heel regelmatig rechthoekig stratenplan.
Steden als Chicago, Denver en ook Manhattan in New York kennen zo'n plattegrond.
Je kunt dan op verschillende manieren van het éne punt naar het andere gaan zonder dat je er langer over doet of omwegen maakt. Hoeveel routes kun je kiezen?
Je leert nu:
- mogelijke routes zonder omwegen tellen in een rooster;
- de driehoek van Pascal gebruiken.
Je kunt al:
- werken met tabellen en diagrammen om mogelijkheden te tellen;
- machten en permutaties toepassen bij telproblemen met of zonder herhaling;
- permutaties en combinaties toepassen bij het kiezen van r elementen uit n elementen.
Verkennen

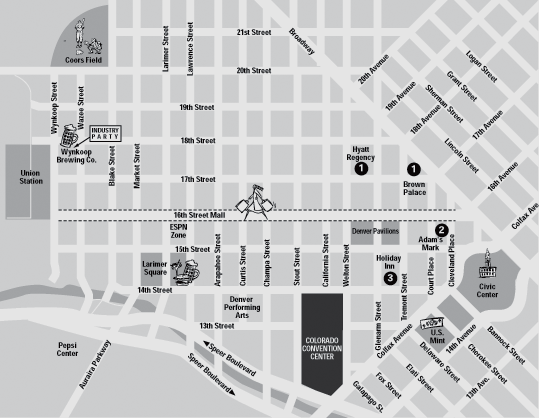
Hier zie je een stratenplan van het centrum van Denver, een grote stad in de USA.
Je staat op Larimer Square op de hoek van Larimer Street en 15th Street.
Je hotel is Hyatt Regency.
> Uit hoeveel even lange routes (zonder omwegen) kun je kiezen?
Uitleg
Uitleg
Hierboven zie je een stukje stratenplan van Denver, USA.
Je wilt van de hoek van Larimer Street en 15th Street naar de Wynkoop Brewing Co, op de hoek van 18th Street en Wynkoop Street. Hoeveel even lange routes (zonder omwegen) kun je kiezen?
Hieronder de mogelijke routes: 4 blokken West en 3 blokken Noord. Daarnaast zie je hoe je ze kunt tellen. Het aantal routes in een punt is telkens het aantal routes dat in het punt eronder en dat er rechts naast bij elkaar komt opgeteld.
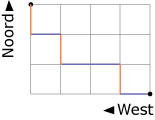
In dit geval kun je het aantal routes wel sneller berekenen. Het zijn namelijk allemaal rijtjes van het type WNWWNWN waarin W een blok naar het Westen en N een blok naar het Noorden voorstelt. Je kiest daarbij 3 posities uit de 7 mogelijke posities om een N neer te zetten. Het aantal manieren is: `((7),(3)) = 35` mogelijkheden.
‡
Opgaven
-
In de Uitleg zie je hoe je het aantal manieren kunt tellen om in Denver van de hoek van Larimer Street en 15th Street naar de Wynkoop Brewing Co te komen.
-
Bekijk de vraag bij Verkennen.
Teken een daarbij passend rooster.
Laat door tellen in dit rooster zien op hoeveel manieren je van Larimer Square naar het Hyatt Regency kunt komen.
-
Op hoeveel manieren kun je van Larimer Square (hoek Larimer Street en 15th Street) naar het kruispunt van Arapahoe Street en 20th Street?
-
Op hoeveel manieren kun je van Larimer Square (hoek Larimer Street en 15th Street) naar het kruispunt van Arapahoe Street en 20th Street via het Hyatt Regency?
Theorie
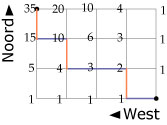
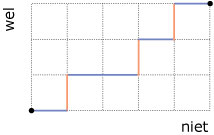
Hier zie je een rooster van 5 bij 3. Er zijn in elk roosterpunt twee keuzes: je gaat richting "wel" of richting "niet".
Je kunt het aantal routes zonder omwegen tellen van het punt linksonder naar dat rechtsboven.
Elke route (zonder omwegen en vanaf linksonder) bestaat uit een rijtje als NWNNWNWN, 3 keer "wel" en 5 keer "niet".
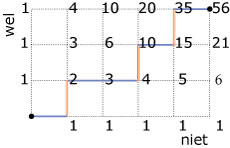
Het aantal routes naar een punt is telkens het aantal routes dat in het punt eronder en dat er links naast bij elkaar komt opgeteld.
Het is de som van de routes van de twee voorgangers.
Je kunt dat in de figuur gemakkelijk natellen als je bedenkt dat je (kortste routes) alleen naar rechts en omhoog kunt bewegen over de roosterlijnen.
Dit telpatroon staat bekend als de driehoek van Pascal.
(Meer hierover bij "Totaalbeeld".)
Je kunt het aantal rijtjes NWNNWNWN ook tellen met behulp van combinaties.
Je moet dan 3 uit de 8 posities kiezen om een W neer te zetten, daarbij speelt volgorde binnen het groepje van 3 W's geen rol. (En binnen het groepje N'en ook niet.)
Je vind dan `((8),(3)) = 56` mogelijkheden.
‡
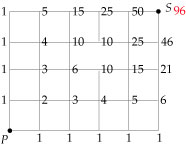
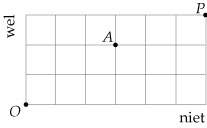
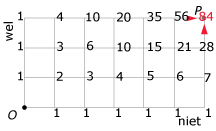
Voorbeeld 1
Hoeveel mogelijke routes (zonder omwegen) zijn er van O naar P?
En hoeveel daarvan gaan langs punt A?
Antwoord
Je kunt het aantal routes van O naar P tellen met de driehoek van Pascal.
Je kunt ook werken met combinaties:
het aantal routes is `((9),(6)) = 84`.
Ook de routes langs A kun je tellen met de driehoek van Pascal. Bedenk dan wel dat de roosterpunten rechts van A geen routes van onder af erbij krijgen en dat de roosterpunten boven A geen routes van links erbij krijgen (anders maak je omwegen).
Ook nu gaat het sneller met combinaties:
- het aantal routes van O naar A is `((5),(3)) = 10`
- het aantal routes van O naar A is `((4),(3)) = 4`
- Het aantal routes via A is `10 * 4 = 40`.
‡
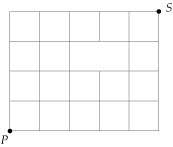
Voorbeeld 2
Hoeveel mogelijke routes (zonder omwegen) zijn er van P naar S?
Antwoord
Je hebt vast wel gezien dat er tussen twee roosterpunten geen weg is.
Dus gewoon even het aantal combinaties van 5 uit 9 uitrekenen levert nu niet het goede antwoord...
Je kunt nu eigenlijk alleen maar het aantal routes uittellen met behulp van het telsysteem van de driehoek van Pascal.
Let goed op wat er in de roosterpunten bij de ontbrekende weg gebeurt.
‡
Voorbeeld 3
Als je met 5 geldstukken werpt dan zijn er nogal wat mogelijkheden.
Er kan bijvoorbeeld 5 keer "munt" boven liggen, maar dat kan ook 2 keer zijn (of nog wat anders) en dit kan telkens andere geldstukken betreffen. Hoeveel mogelijkheden zijn er in totaal?
Antwoord
Zo vind je alle 32 mogelijkheden:
- 5 keer M en 0 keer K: `((5),(5)) = 1` mogelijkheid (MMMMM)
- 4 keer M en 1 keer K: `((5),(4)) = 5` mogelijkheden (MMMMK, MMMKM, MMKMM, etc.)
- 3 keer M en 2 keer K: `((5),(3)) = 10` mogelijkheden (MMMKK, MMKMK, MKMMK, etc.)
- 2 keer M en 3 keer K: `((5),(2)) = 10` mogelijkheden (MMKKK, MKKMK, KKMMK, etc.)
- 1 keer M en 4 keer K: `((5),(1)) = 5` mogelijkheden (MKKKK, KKKMK, KKMMK, etc.)
- 0 keer M en 5 keer K: `((5),(0)) = 1` mogelijkheid (KKKKK)
Een simpel wegendiagram is nu veel handiger.
Elke munt heeft namelijk 2 mogelijkheden, K of M.
Bij 6 munten zijn er dus in totaal 25 = 32 mogelijkheden.
‡
Opgaven
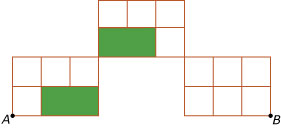
 Bekijk Voorbeelden 1 en dan het rooster hiernaast.
Bekijk Voorbeelden 1 en dan het rooster hiernaast.
-
Hoeveel kortste routes zijn er van `A` naar `B`?
-
Hoeveel kortste routes zijn er van `A` naar `P`? En van `P` naar `B`?
-
Hoeveel kortste routes zijn er van `A` naar `B` via `P`?
-
Ga uit van een systeem met 7 schakelaars die allemaal 'aan' of 'uit' kunnen staan.
- Teken een bijpassend rooster om in te tellen.
- Laat in het rooster zien op hoeveel manieren je 0 van de 7 schakelaars kunt aanzetten.
- Op hoeveel manieren kun je 1 van de 7 schakelaars aanzetten?
- Op hoeveel manieren kun je 2 van de 7 schakelaars aanzetten?
- Je hebt de eerste drie schakelaars aangezet. Op hoeveel manieren kun je er nu nog 2 van de resterende 4 aanzetten?
 Bekijk nu Voorbeeld 2.
Bekijk nu Voorbeeld 2.
Op hoeveel manieren kun je in dit rooster van `A` naar `B`?
-
Bekijk Voorbeeld 3.
Teken hierbij een rooster om in te tellen. Geef er in aan hoe je het aantal mogelijkheden kunt vinden met drie keer "munt".
-
Oudere computers werkten met een 8-bits codesysteem.
Elk teken ("byte" genoemd) werd daarin voorgesteld door een code van acht nullen en énen.
Bijvoorbeeld werd de hoofdletter A (het 65e teken) voorgesteld door: 01000001.
- Hier zie je een byte. Geef het teken aan met nullen en énen in de juiste volgorde.
- Hoeveel bytes zijn er met precies vier nullen?
- Hoeveel bytes zijn er met meer dan vier nullen?
- Hoeveel bytes kun je in totaal maken?
Verwerken
-
Je gooit met 10 geldstukken en let op het aantal keren "kruis" dat boven komt.
- Op hoeveel manieren krijg je 3 keer "kruis"?
- Hoeveel mogelijkheden zijn er in totaal?
- Op hoeveel manieren krijg je minstens 8 keer "kruis"?
- Op hoeveel manieren krijg je hoogstens 8 keer "kruis"?
-
Het bestuur van een sportclub bestaat uit 6 leden.
Als ze vergaderen geven sommigen elkaar vooraf een hand.
- Teken een rooster om alle mogelijkheden te tellen voor iemand die twee willkeurige personen de hand wil schudden.
- Hoeveel mogelijkheden heeft hij?
- Hoeveel mogelijkheden zijn er voor hem in totaal?
-
Een vertegenwoordiger moet deze week nog 14
klanten bezoeken. Die klanten zijn allemaal ongeveer even ver van zijn woonplaats
verwijderd. Hij besluit de eerste dag bij 4 klanten langs te gaan.
-
Op hoeveel manieren kan hij 4 uit de 14 klanten zoeken?
-
De tweede dag doet hij maar twee klanten aan, want dan kan hij die dag ook aan zijn administratie werken.
Op hoeveel manieren kan hij die uitzoeken?
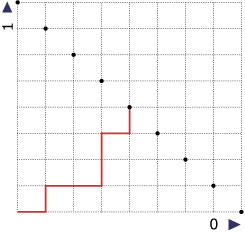
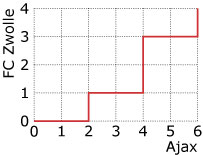 Bij de voetbalwedstrijd Ajax–FC Zwolle was de uitslag 6–4. Het scoreverloop wordt in de figuur hiernaast weergegeven.
Bij de voetbalwedstrijd Ajax–FC Zwolle was de uitslag 6–4. Het scoreverloop wordt in de figuur hiernaast weergegeven.
- Schrijf het scoreverloop op door alle tussenstanden achter elkaar te zetten.
- Als je alleen de uitslag weet, hoeveel scoreverlopen zijn dan mogelijk?
- Behalve de einduitslag (6–4) weet je ook de stand met de pauze (4–1).
Hoeveel scoreverlopen zijn nu nog mogelijk?
-
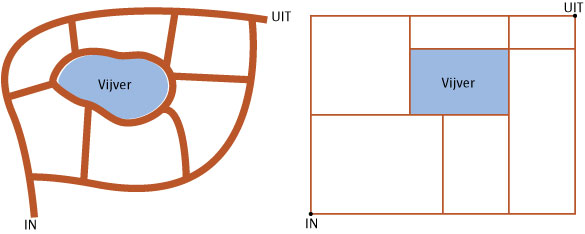
Je ziet hier een tuin met paden en een vijver. Deze plattegrond kun je schematisch
weergeven in een rechthoekig rooster, zie de figuur hieronder.
Bereken nu met behulp van dit rooster het aantal routes zonder omwegen dat je kunt
lopen van de ingang naar de uitgang.
-
Je ziet hier het morsealfabet.
Elke letter bestaat uit maximaal 4 signalen; elk cijfer bestaat uit precies 5 signalen.
Een signaal kan zijn 'kort' (aangegeven door - ) of 'lang' (aangegeven door —).

-
Hoeveel tekens zijn er mogelijk met vijf signalen?
-
Hoeveel tekens zijn er mogelijk met maximaal vier signalen?
-
Het is ook mogelijk om alle cijfers weer te geven met twee punten en drie strepen.
Laat dat zien door alle mogelijkheden systematisch op te schrijven.
Testen
-
Een groep van twaalf personen wordt verdeeld in twee teams van zes. Ze besluiten de verdeling uitsluitend van het toeval te laten afhangen.
Op hoeveel manieren kunnen ze de twee teams samenstellen?
 Speciaal voor blinden en slechtzienden bestaat het Brailleschrift. In het Brailleschrift ontstaat elk teken om van zes mogelijke punten er een aantal in reliëf weer te geven opdat een blinde het aantal en de positie van de punten kan voelen en zo het teken herkennen. Hier zie je het alfabet en de cijfers in Braille.
Speciaal voor blinden en slechtzienden bestaat het Brailleschrift. In het Brailleschrift ontstaat elk teken om van zes mogelijke punten er een aantal in reliëf weer te geven opdat een blinde het aantal en de positie van de punten kan voelen en zo het teken herkennen. Hier zie je het alfabet en de cijfers in Braille.

- Op hoeveel manieren kun je kun je een Brailleteken maken met twee punten in reliëf?
- Op hoeveel manieren kun je kun je een Brailleteken maken met drie punten in reliëf?
- Hoeveel Brailletekens zijn er mogelijk?
- Er zijn Brailletekens die op de kop hetzelfde zijn. Hoeveel Brailletekens met twee punten betreft dit?
-
Bepaal in dit rooster het aantal kortste routes van `A` naar `B`.






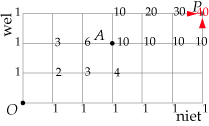


 Bekijk Voorbeelden 1 en dan het rooster hiernaast.
Bekijk Voorbeelden 1 en dan het rooster hiernaast.
 Bekijk nu Voorbeeld 2.
Bekijk nu Voorbeeld 2. 
 Bij de voetbalwedstrijd Ajax–FC Zwolle was de uitslag 6–4. Het scoreverloop wordt in de figuur hiernaast weergegeven.
Bij de voetbalwedstrijd Ajax–FC Zwolle was de uitslag 6–4. Het scoreverloop wordt in de figuur hiernaast weergegeven.


 Speciaal voor blinden en slechtzienden bestaat het Brailleschrift. In het Brailleschrift ontstaat elk teken om van zes mogelijke punten er een aantal in reliëf weer te geven opdat een blinde het aantal en de positie van de punten kan voelen en zo het teken herkennen. Hier zie je het alfabet en de cijfers in Braille.
Speciaal voor blinden en slechtzienden bestaat het Brailleschrift. In het Brailleschrift ontstaat elk teken om van zes mogelijke punten er een aantal in reliëf weer te geven opdat een blinde het aantal en de positie van de punten kan voelen en zo het teken herkennen. Hier zie je het alfabet en de cijfers in Braille.
