Combinaties

Inleiding

Je hebt kennis gemaakt met systematisch tellen, zowel met behulp van diagrammen als met behulp van machten en permutaties. Het aantal permutaties van 3 uit 8 is het aantal manieren om drie verschillende elementen uit een totaal van 8 te halen. Maar vaak heb je niet allemaal verschillende elementen, maar groepjes dezelfde elementen. Daar gaat het nu over...

Je leert nu:

• het verschil onderscheiden tussen permutaties en combinaties;
• het aantal combinaties van r uit n elementen berekenen.

Je kunt al:

• werken met tabellen en diagrammen om mogelijkheden te tellen;
• machten en permutaties toepassen bij telproblemen met of zonder herhaling.

Verkennen

Acht hardlopers doen mee aan een wedstrijd over 100 meter. Ga ervan uit dat hun volgorde van aankomst uitsluitend van het toeval afhangt.

> Op hoeveel manieren kunnen deze acht hardlopers als eerste, als tweede en als derde aankomen?
> De eerste drie gaan door naar de volgende ronde. Hoeveel mogelijke drietallen zijn dat?

Uitleg

Bij de Olympische Spelen is de 100 m hardlopen een vast onderdeel. In de finale starten 8 lopers A, B, C, D, E, F, G en H. Ze strijden om goud, zilver of brons. Stel je voor dat alle lopers gelijkwaardig zijn en een even grote kans maken op de medailles.
Hoeveel mogelijke lijstjes met drie medaillewinnaars kun je dan maken?

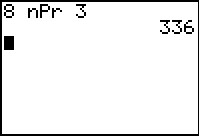
Het gaat hier om het aantal permutaties van 3 uit 8: 8 · 7 · 6 = `(8!)/(5!)` = 336 mogelijkheden.

In de voorrondes is het niet belangrijk of je nummer 1, nummer 2 of nummer 3 bent: de eerste drie gaan door naar de volgende ronde. De lijstjes BDG, BGD, DBG, GBD, DGB en GDB hebben dan allemaal hetzelfde resultaat. Die tellen dan dus niet als afzonderlijke mogelijkheden, maar vormen samen één mogelijkheid.
En dat geldt ook voor alle andere drietallen: de volgorde binnen die drietallen is niet belangrijk en die 3! volgordes tellen telkens maar als één mogelijkheid mee. Dit betekent dat er geen 336 mogelijke lijstjes zijn, maar slechts 336 gedeeld door 3!.

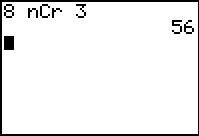Je spreekt dan van het aantal combinaties van 3 uit 8. Je schrijft het als `((8),(3))`.
Je rekent het aantal combinaties van 3 uit 8 zo uit: `((8),(3)) = (8*7*6)/(3!) = (8*7*6)/6 = 56` mogelijkheden.
De rekenmachine heeft ook hiervoor een speciale functie.

‡

Opgaven

1. Bestudeer de Uitleg. Bekijk goed wat je verstaat onder het aantal combinaties van 3 uit 8.
   1. Wat is het kenmerkende verschil tussen de finale en de voorrondes?
   2. Waarom werk je in de voorrondes met combinaties als je alle mogelijke eindresultaten wilt berekenen?
   3. Bereken zelf met de hand het aantal combinaties van 3 uit 8.
   4. Bekijk bij Practicum GR hoe je dit met de grafische rekenmachine kunt uitrekenen.
   5. Bereken eerst met de hand het aantal combinaties van 3 uit 100. Controleer het antwoord met de GR.

Theorie

Als je 3 verschillende elementen kiest uit 8 beschikbare dan heb je `(8!)/(3!)` mogelijkheden.

Dit heet het aantal permutaties van 3 elementen uit 8 elementen.

Als je 3 elementen kiest uit 8 beschikbare en hun onderlinge volgorde is niet van belang dan heb je `((8),(3)) = (8*7*6)/(3!)` mogelijkheden.

Dit heet het aantal combinaties van 3 elementen uit 8 elementen.

‡

Voorbeeld 1

In een klas van 24 personen wordt door loting een groep van 4 personen samengesteld. Deze vier personen krijgen elk een andere taak.
Op hoeveel manieren kan dit als er per taak wordt geloot?

Antwoord

Nu is de volgorde in de groep die wordt geloot van belang: ben je als eerste ingeloot dan heb je een andere taak dan wanneer je als tweede, of derde of vierde wordt ingeloot.

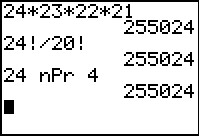
Het gaat nu dus om het aantal permutaties van 4 uit 24.

Er zijn daarom `24 * 23 * 22 * 21 = 255024` mogelijkheden.

‡

Voorbeeld 2

In een klas van 24 personen wordt door loting een groep van 4 personen samengesteld. Deze vier personen krijgen elk een andere taak.
Op hoeveel manieren kan dit als deze vier personen pas na de loting hun taken onderling verdelen?

Antwoord

Nu is de volgorde in de groep die wordt geloot niet van belang: ze verdelen pas na de loting onderling hun taken.

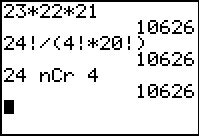
Het gaat nu dus om het aantal combinaties van 4 uit 24.

Er zijn daarom `((24),(4)) = (24*23*22*21)/(4!) = 23*22*21 = 10626` mogelijkheden.

‡

Voorbeeld 3

Uit een groepje van 5 meisjes en 4 jongens kies je door loting een drietal.
Hoeveel mogelijkheden zijn er als daar daar minstens 2 meisjes bij zijn?

Antwoord

Minstens 2 meisjes betekent dat er 2 meisjes of 3 meisjes bij moeten zijn.

Als er precies 2 meisjes bij moeten zijn, dan kun je bijvoorbeeld eerst 2 van de 5 meisjes kiezen en vervolgens 1 van de 4 jongens.
De 2 meisjes kies je op `((5),(2)) = 10` manieren.
Bij elk van deze 10 mogelijkheden zijn er nog eens `((4),(1)) = 4` mogelijke keuzes voor 1 jongen.
Dus zijn er in totaal `10 * 4 = 40` mogelijkheden om precies 2 meisjes te kiezen.

Als er precies 3 meisjes bij moeten zijn, hoef je alleen maar 3 van de 5 meisjes te kiezen.
Dat kun je op `((5),(3)) = 10` manieren doen.

In totaal zijn er dus `40 + 10 = 50` manieren om minstens 2 meisjes te kiezen.

‡

Opgaven

2. Bekijk de Voorbeelden 1 en 2. Vergelijk de verschillen!
   Je hebt een groep van 20 personen, 8 mannen en 12 vrouwen.
   1. Uit de groep van 20 worden door loting vijf personen gehaald. Elk van hen krijgt een bepaalde opdracht. Op hoeveel manieren kan dat als ze de opdrachten na de loting onderling verdelen?
   2. Uit de groep van 20 worden door loting vijf personen gehaald. Elk van hen krijgt een bepaalde opdracht. Op hoeveel manieren kan dat als er per opdracht wordt geloot?


3. Bekijk nu Voorbeeld 3.
   1. Reken zelf de in het voorbeeld gevraagde kans nog eens na.
   2. Op hoeveel manieren kun je door loting uit een groep van 20 met 8 mannen en 12 vrouwen een groep van vijf samenstellen die bestaat uit 3 mannen en 2 vrouwen?
   3. Op hoeveel manieren kun je door loting uit een groep van 20 met 8 mannen en 12 vrouwen een groep van vijf samenstellen die bestaat uit hoogstens 3 mannen?


4. Ga uit van een systeem met 7 schakelaars die allemaal 'aan' of 'uit' kunnen staan.
   1. Op hoeveel manieren kun je 0 van de 7 schakelaars aanzetten?
   2. Op hoeveel manieren kun je 1 van de 7 schakelaars aanzetten?
   3. Op hoeveel manieren kun je 2 van de 7 schakelaars aanzetten?
   4. Het aantal manieren om 3 van de 7 schakelaars aan te zetten is gelijk aan het aantal manieren om er 4 van de 7 aan te zetten. Leg uit waarom dat zo is.


5. Stel je voor dat er 30 schakelaars zijn (die 30 toneellampen bedienen), waarmee je de belichting op een podium kunt regelen. Voor een bepaalde scènemoeten er vier van de 30 worden aangezet. Neem eerst aan dat de volgorde waarin ze worden aangezet wel van belang is.
   1. Op hoeveel manieren kun je de eerste schakelaar kiezen?
   2. Op hoeveel manieren kun je vier schakelaars kiezen?
   Stel je nu voor dat het niet van belang is in welke volgorde de schakelaars worden aangezet, alleen maar welke vier er 'aan' staan.
   3. Je moet voor een bepaalde scène de schakelaars `S5`, `S7`, `S8` en `S9` gebruiken. Op hoeveel verschillende manieren kun je die schakelaars nog 'aan' zetten?
   4. Hoe kun je met behulp van de antwoorden op de vragen bij b en c berekenen op hoeveel manieren je vier schakelaars uit de 30 kunt kiezen als de volgorde niet belangrijk is?
   5. Op hoeveel manieren kun je 6 schakelaars kiezen uit de 30 als de volgorde niet belangrijk is?


6. Voor je literatuurlijst moet je uit 40 literaire boeken en 15 thrillers er tien kiezen.
   1. Op hoeveel manieren kan dat als er verder geen eisen aan je lijst worden gesteld?
   2. Op hoeveel manieren kan dat als er maximaal 3 thrillers mogen worden gekozen?

Verwerken

7. Iemand moet 10 vragen met 'ja' of 'nee' beantwoorden.
   1. Hoeveel lijsten met antwoorden zijn er mogelijk met precies drie keer 'ja'?
   2. Hoeveel lijsten met antwoorden zijn er mogelijk met precies 9 keer 'ja'?
   3. Hoeveel lijsten met antwoorden zijn er in totaal mogelijk?


8. Je gooit met vijf verschillende geldstukken en je let op het aantal keren 'kruis'.
   1. Hoeveel verschillende uitkomsten zijn er mogelijk?
   2. Hoeveel mogelijke uitkomsten met precies twee keer 'kruis' zijn er?
   3. Je gooit nu met 50 geldstukken. Op hoeveel manieren kun je 20 keer 'kruis' werpen?


9. Voor een schaaktoernooi hebben zich 24 deelnemers gemeld. Ze spelen een halve competitie, dus elke deelnemer speelt precies één maal tegen iedere andere deelnemer. Het aantal wedstrijden kan nu worden berekend met behulp van combinaties.
   Leg uit waarom dat zo is en bereken het aantal te spelen wedstrijden.
   


10. Een groep bestaat uit 14 meisjes en 12 jongens. Er wordt een groepje van vier door loting uitgekozen.
    1. Als het groepje uitsluitend uit meisjes moet bestaan, hoeveel verschillende groepjes zijn er dan mogelijk?
    2. Beantwoord dezelfde vraag als het groepje uit twee jongens en twee meisjes moet bestaan.


11. Op hoeveel manieren kunnen 8 verschillende boeken op een rij op een boekenplank worden geplaatst als
    1. iedere volgorde is toegestaan?
    2. de drie wiskundeboeken bij elkaar moeten staan?
    3. de twee woordenboeken op het eind van de rij naast elkaar moeten staan?
    4. er drie boeken worden uitgekozen om te worden gekaft en dan aan het eind te worden gezet?


12. Je werpt met drie dobbelstenen en let op het aantal ogen dat boven komt.
    1. Hoeveel verschillende uitkomsten zijn er mogelijk?
    2. Je kunt op verschillende manieren 12 ogen gooien. Bijvoorbeeld door driemaal 4 te gooien, maar ook door een 6 en tweemaal 3 te gooien.
       Hoeveel mogelijkheden zijn er om 12 ogen te gooien?


13. Op een scholengemeenschap bestaat de medezeggenschapsraad uit 18 personen: 9 personeelsleden en 9 ouders en/of leerlingen. Die medezeggenschapsraad kiest een dagelijks bestuur van vier personen.
    1. Op hoeveel manieren kan dat als er verder geen eisen aan dat dagelijks bestuur worden gesteld?
    2. Op hoeveel manieren kan dat als er evenveel personeelsleden als ouders en/of leerlingen in moeten zitten?
    3. Op hoeveel manieren kan dat als eerst de voorzitter, dan de vice-voorzitter, vervolgens de secretaris en tenslotte de penningmeester in functie worden gekozen?

Testen

14. Een volleybalteam bestaat uit 12 spelers. De coach bepaalt welke spelers worden opgesteld en op welke van de zes posities in het veld.
    1. Als alle spelers even sterk zijn en op elke positie kunnen spelen, op hoeveel manieren kan de coach dan een team van zes samenstellen?
    2. Als hij dat team heeft samengesteld, hoeveel verschillende beginopstellingen kan hij dan nog maken?


15. Een klas bestaat uit 26 leerlingen.
    1. Op hoeveel manieren kun je al die leerlingen op een rij zetten?
    2. Op hoeveel manieren kun je 5 van de 26 leerlingen op een rij zetten?
    3. Op hoeveel manieren kun je een groepje van 5 uit de 26 kiezen?
    4. Er zitten 10 meisjes in deze klas. Op hoeveel manieren kun je een groepje van 5 leerlingen kiezen als daar precies twee meisjes in moeten voorkomen?