Mogelijkheden

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Tellen > Mogelijkheden > Inleiding

Probeer de vraag bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Tellen > Mogelijkheden > Uitleg

Opgaven

1. Bestudeer de Uitleg.
   1. Wat is het verschil tussen een boomdiagram en een wegendiagram?
   2. Wat is het voordeel van een boomdiagram?


2. Je hebt in een hoge hoed vier kaartjes met daarop de letters A, B, C, D. Je haalt die kaartjes er aselect één voor één uit. Hoeveel mogelijke volgordes zijn er? (Maak een boomdiagram!)

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Tellen > Mogelijkheden > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. Iemand heeft dobbelstenen in de vorm van een regelmatig viervlak. Op de grensvlakken staan de cijfers 1, 2, 3 en 4. Elk vlak heeft een gelijke kans om 'onder' te komen als je met zo’n dobbelsteen gooit. Er wordt geworpen met drie van die dobbelstenen, een rode, een groene en een witte. We letten op de vlakken die 'onder' komen na het werpen. Kijk ook bij Voorbeeld 1.
   1. Geef in een wegendiagram alle mogelijke uitkomsten weer. Hoeveel mogelijkheden zijn er in totaal?
   2. Je wilt het aantal uitkomsten tellen waarbij precies één keer het cijfer 3 onder ligt. Waarom zijn er 9 mogelijkheden waarbij alleen bij de rode dobbelsteen de 3 onder ligt?
   3. Hoeveel mogelijkheden zijn er waarbij bij de rode of de groene dobbelsteen de 3 onder ligt?
   4. Hoeveel mogelijkheden zijn er waarbij precies één keer de 3 onder ligt?


4. Bij het werpen met twee dobbelstenen kun je de mogelijkheden overzichtelijk weergeven in een rooster. Zie Voorbeeld 2.
   1. Waarom gaat dat bij het werpen met drie dobbelstenen niet?
   2. Je werpt met twee dobbelstenen.
      Op hoeveel manieren kunnen er 9 ogen boven komen?
   3. Je werpt met drie dobbelstenen.
      Op hoeveel manieren kunnen er 9 ogen boven komen?


5. Je hebt vier uiterlijk gelijke briefjes met daarop de namen Paul, Anja, Frits en Elly. De briefjes worden in een vaas gedaan, je moet er twee kiezen. Zie ook Voorbeeld 2.
   1. Teken bij deze situatie een rooster.
   2. Laat zien dat een boomdiagram dezelfde mogelijkheden geeft.
   3. In hoeveel gevallen kies je zowel Paul als Anja?


6. Bekijk het wegendiagram bij Voorbeeld 3. Je kunt van C naar D via A of via B, in A en in B moet je dan overstappen.
   1. Op hoeveel manieren kun je van C naar D via A?
   2. Op hoeveel manieren kun je van C naar D via B?
   3. Op hoeveel manieren kun je van C naar D?
   4. Hoe heb je hierbij gebruik gemaakt van de vuistregels beschreven in het voorbeeld?


7. Bij de PINcode gaat het om een code van vier cijfers (0, 1, 2, .., 9). Ga er van uit dat voor elk cijfer waaruit de PINcode bestaat alle mogelijkheden zijn toegestaan.
   1. Hoe bereken je met een wegendiagram hoeveel codes van vier cijfers er mogelijk zijn?
   2. Als het eerste cijfer geen 0 is, hoeveel PINcodes zijn er dan nog mogelijk?
   Van je PINcode weet je alleen nog dat de cijfers 1, 7 en 7 erin voorkomen in die volgorde. Het vierde cijfer (voorgesteld door een *) is geen 1 en geen 7, en de plaats er van is niet duidelijk. Mogelijke PINcodes zien er dan zo uit: 1 7 7 * of 1 7 * 7 of 1 * 7 7 of * 1 7 7.
   1. Hoeveel PINcodes zijn er mogelijk op die manier?

Verwerken

8. Een toets bestaat uit 6 meerkeuzevragen. Op elke meerkeuzevraag kun je uit vier antwoorden kiezen; er is telkens maar één antwoord goed.
   1. Geef in een wegendiagram alle mogelijkheden weer.
   2. Hoeveel mogelijke series antwoorden zijn er?
   3. Je hebt de toets goed voorbereid en je weet 4 antwoorden zeker. Hoeveel mogelijke series antwoorden zijn er nu nog?
   4. Als je alleen let op 'goed' of 'fout', hoveel series antwoorden zijn dan mogelijk?


9. Om het cijferslot van een koffer open te krijgen moet je een code van vier cijfers onthouden.
   1. Je weet alleen het eerste cijfer nog. Hoeveel mogelijke codes zijn er dan nog?
   2. Je weet alle vier de cijfers nog, maar de volgorde niet meer. Hoeveel mogelijke codes zijn er?


10. Je werpt met drie gewone dobbelstenen.
    1. Geef in een wegendiagram alle mogelijke uitkomsten weer.
    2. Waarom is een boomdiagram niet zo geschikt in dit geval?
    3. Bij hoeveel mogelijke uitkomsten heb je precies één zes?
    4. Bij hoeveel mogelijke uitkomsten heb je twee zessen?
    5. Bij hoeveel mogelijke uitkomsten heb je drie zessen?
    6. Bij hoeveel mogelijke uitkomsten heb je minstens twee zessen?
    7. Bij hoeveel mogelijke uitkomsten heb je hoogstens twee zessen?


11. Je bestelt een pizza bij Mario. Je hebt keuze uit een kleine pizza, een gewone pizza en een extra grote pizza. Er zijn twee soorten pizzabodem: de "pizza crossa" en de "pizza classico". Verder zijn er 12 verschillende smaken.
    Je kunt de pizza zelf halen of je kunt hem laten bezorgen.
    1. Uit hoeveel verschillende pizza's kun je bij Mario kiezen?
    2. Hoeveel keuzemogelijkheden heb je in totaal als je een pizza van Mario wilt eten?
    3. Je houdt niet van vis. Daarom vallen er 5 smaken af. Uit hoeveel verschillende pizza's kun je nu nog kiezen?


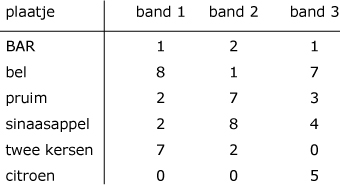12. Een fruitautomaat heeft drie vensters waarachter banden met plaatjes draaien. Op elke band staan 20 plaatjes en je brengt ze in beweging door aan een hendel te trekken. Eén druk op de knop en de banden stoppen. Zie je nu drie dezelfde plaatjes dan win je een bepaald bedrag. Van de plaatjes is per band het aantal op die band als volgt aangegeven:
    1. Hoeveel mogelijkheden zijn er in totaal?
    2. Op hoeveel manieren kun je drie keer BAR krijgen?
    3. Op hoeveel manieren kun je drie keer 'sinaasappel' krijgen?
    4. Op hoeveel manieren kun je drie keer 'twee kersen' krijgen?
    5. Hoeveel winstmogelijkheden zijn er?

Testen

13. Op vakantie naar de zon neem je vooral luchtige kleding mee. Bijvoorbeeld: 2 paar schoenen, 6 paar sokken, 4 korte broeken en 5 shirts.
    1. Teken een wegendiagram van alle mogelijke combinaties van schoenen, sokken, broek en shirt.
    2. Op hoeveel verschillende manieren kun je je zomers kleden?
    3. Op het strand heb je geen sokken en schoenen aan. Op hoeveel verschillende manieren kun je daar luchtig gekleed vertoeven?


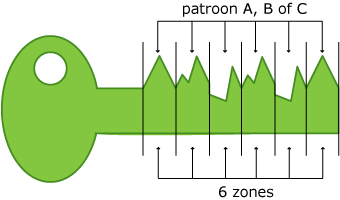14. Voor cilindersloten worden verschillende soorten sleutels gemaakt. De sleutel die je hier ziet bestaat uit zes gedeelten. Voor elk gedeelte wordt één van de patronen A, B of C gekozen.
    Hoeveel verschillende sleutels van deze soort zijn er mogelijk?
    


15. Een deelnemer aan een tv-quiz krijgt vier kaarten met op ieder een naam van een populaire zangeres. Zijn opdracht is om deze kaarten onder de foto’s van deze zangeressen te hangen, de juiste naam bij elke foto. Deze deelnemer kent geen van de vier zangeressen en besluit op goed geluk de kaarten neer de hangen.
    1. Geef in een boomdiagram alle mogelijkheden weer.
    2. Hoeveel mogelijkheden heeft hij in totaal?
    3. Op hoeveel manieren heeft hij één kaart goed?