Vearanderingen in grafieken

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Veranderingen > In grafieken > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Gebruik de website www.getij.nl.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Veranderingen > In grafieken > Uitleg

Opgaven

1. Bekijk de grafiek van de gemiddelde dagtemperatuur in de Uitleg.
   1. Als de grafiek stijgend is, neemt `T` dan toe of juist af?
   2. Als de grafiek toenemend stijgend is, wat gebeurt er dan met `T`?
   3. Wat is voor de grafiek het verschil tussen een toenemende daling en een afnemende daling? En wat betekent dit voor de temperatuur `T`?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Veranderingen > In grafieken > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

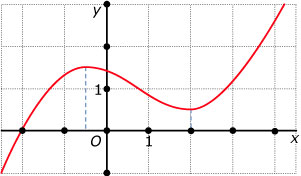2. Hier zie je dezelfde grafiek als in de Theorie, pagina 1. Nu staan er eenheden bij de assen.
   1. De grafiek is stijgend op:
      1. `(:larr,1:)` en `(:4,rarr:)`
      2. `(:larr;-0,5:)` en `(:2,rarr:)`
      3. `(:-1,4:)`
      4. `(:-0,5;2:)`
   2. Er is sprake van toenemende daling op:
      1. `(:-0,5;0,75:)`
      2. `(:0,75;2:)`
   3. Op welk interval is er sprake van toenemende stijging?
   4. Schrijf de waarde van het lokale minimum op.


3. In de Voorbeelden 1 en 2 vind je hoe je de veranderingen van de grafiek van een functie beschrijft.
   Gegeven is de kwadratische functie `y = -x^2 + 6x`. De grafiek van zo’n functie is een parabool.
   1. Met de grafische rekenmachine kun je de parabool bekijken. Op welk interval is de grafiek stijgend?
   2. Om welke soort stijging gaat het bij a?
      1. toenemende stijging
      2. afnemende stijging
      3. constante stijging
   3. Is er in de grafiek sprake van toenemende of afnemende daling?
   4. Elke parabool heeft een top. Daarbij hoort een minimum of een maximum. Welke extreme waarde heeft deze functie?
      1. Een minimum `(3,9)`.
      2. Een minimum van 9 voor `x=3`.
      3. Een maximum `(3,9)`.
      4. Een maximum van 9 voor `x=3`.


4. Uit een beschrijving van de verandering van een functie kun je vaak de grafiek afleiden. In Voorbeeld 3 wordt dat toegelicht, hier kun je het zelf proberen. Van een functie is gegeven dat
   • de grafiek constant stijgt tot `x=2`;
   • de grafiek constant is vanaf `x=2` tot aan `x=3`;
   • de grafiek toenemend daalt vanaf `x=3` tot `x=4` en dan toenemend daalt tot `x=5`;
   • de grafiek toenemend stijgt vanaf `x=5`.
   Maak een schets van de grafiek van deze functie en leg uit bij welke waarde van `x` de functie een uiterste waarde moet hebben.
   


5. Je gebruikt nu steeds een grafiek om de veranderingen en de extremen van een functie te bepalen.
   Waarom kun je op deze manier nooit zeker zijn of je wel alle veranderingen en extremen hebt gevonden?

Verwerken

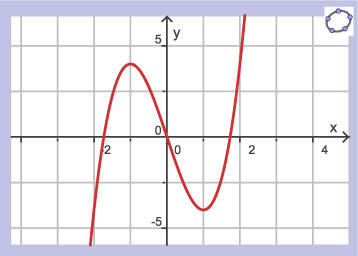6. Je ziet hier de grafiek van een functie.
   Schrijf voor deze functie op
   • op welke intervallen de grafiek dalend dan wel stijgend is en om welk soort stijging of daling het daarbij gaat;
   • welke extremen er zijn;
   • voor welke waarden van `x` de snelheid van dalen dan wel stijgen het grootst is.


7. Gegeven is een functie met voorschrift `y = 18x - x^3`.
   Schrijf op
   • op welke intervallen de grafiek dalend dan wel stijgend is en om welk soort stijging of daling het daarbij gaat;
   • welke extremen er zijn;
   • voor welke waarden van `x` de snelheid van dalen dan wel stijgen het grootst is.


8. Gegeven is de functie `y = 0,5*x^4 - 4*x^2 + 8`.
   1. Met de grafische rekenmachine kun je de grafiek van deze functie bekijken. Welke extremen heeft deze functie?
   2. Er is precies één interval waarop de grafiek toenemend daalt. Welk interval is dat?


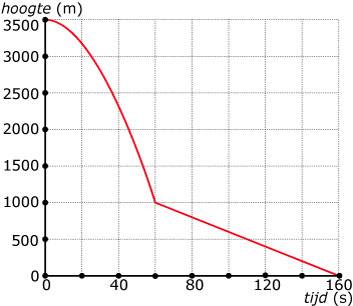9. Je ziet hier de grafiek die hoort bij een parachutesprong vanaf 3500m hoogte. Eerst maakt hij een vrije val en daarna opent hij zijn parachute.
   1. Na hoeveel seconden heeft deze parachutist zijn valscherm geopend? Hoe zie je dat aan de grafiek?
   2. In de periode van vrije val is de grafiek toenemend dalend.Wat betekent dit voor de valsnelheid?
   3. Als de parachute uit is, is de valsnelheid constant. Hoe zie je dat aan de grafiek? Hoe groot is de valsnelheid als de parachute uit is?


10. Voor de temperatuur `T` in °C op een bepaalde dag geldt:
    • om 6:00 uur ’s morgens (`t = 6`) bedroeg de temperatuur `T = 2`°C;
    • de grafiek toenemend stijgt vanaf `t = 6` tot aan `t = 12`;
    • de grafiek afnemend stijgt vanaf 12:00 uur tot 14:30 uur en dan toenemend daalt tot `t = 20`;
    • de grafiek afnemend daalt vanaf `t = 20` tot aan het eind van de dag.
    Maak een schets van een mogelijke grafiek van deze functie en leg uit bij welke waarde van `t` de functie `T` een uiterste waarde moet hebben.

Testen

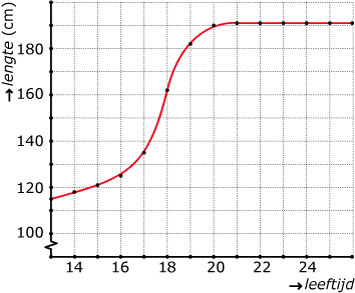
11. Je ziet hier de grafiek van de lengte van een man vanaf zijn twaalfde levensjaar tot zijn huidige leeftijd.
    
    
    
    
    1. Gedurende welk levensjaar groeit hij het snelst? Hoeveel cm groeide hij dat jaar?
    2. Gedurende welke periode is de grafiek stijgend?
    3. Gedurende welke periode is er sprake van een afnemende stijging?
    4. Gedurende welke periode is zijn lengte constant?
    5. Gedurende welke perioden is de groeisnelheid constant? Hoe zie je dat aan de grafiek?


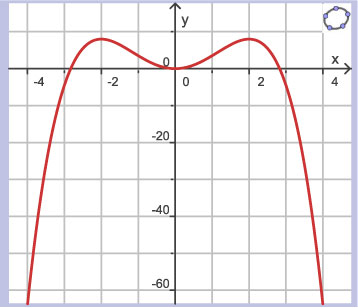12. Je ziet hier de grafiek van de functie `y = -0,5x^4 + 4x^2`op het interval `[-4,4]`.
    1. Op welke intervallen is de grafiek dalend?
    2. Op welk interval is er sprake van een afnemende daling? Hoe zie je dat aan de grafiek?
    3. Schrijf alle extremen op van deze functie.