Totaalbeeld

Samenvatten

Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Werken met formules. Een eigen samenvatting maken is nuttig.

Begrippenlijst:

21: verband tussen twee variabelen — functie, invoerwaarde, uitkomst — gelijkwaardige formules
22: grafieken — snijpunten met assen — toppen — asymptoten
23: vergelijking — oplossing van een vergelijking
24: ongelijkheid — oplossing van een ongelijkheid
25: verband tussen drie variabelen — grafiekenbundel

Activiteitenlijst:

21: formules herschrijven (balansmethode) — een variabele uitdrukken in een andere variabele
22: karakteristieken van grafieken bepalen
23: vergelijkingen oplossen met de balansmethode en/of terugrekenen
24: ongelijkheden oplossen
25: grafiekenbundel tekenen — verbanden met meerdere variabelen combineren

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Werken met formules > Totaalbeeld > Achtergronden

Testen

  1. Los deze vergelijkingen algebraïsch op. Geef eventueel benaderingen van je antwoorden in twee decimalen nauwkeurig.
    1. `1220 + 0,35q = 2056 + 0,12q`
    2. `-0,15(x + 25)^2 + 15 = 0`
    3. `4 * t^(12) = 16`
    4. `350/(20+0,25d^2) = 7`

  2. Los de volgende vergelijking op met behulp van de grafische rekenmachine. Geef een benadering in drie decimalen nauwkeurig.
    `x^2 + sqrt(2x) = 20`

  3. Een fabrikant wil zijn hagelslag verpakken in doosjes met een vierkante bodem. Voor een doosje gebruikt hij 800 cm3 karton. Ga ervan uit dat een doosje precies de vorm van een balk heeft.
    1. De hoogte van zo’n doosje wordt aangegeven met `h` en de zijde van het grondvlak met `x`. Laat zien dat het verband tussen `h` en `x` beschreven wordt door de formule: `4xh + 2x^2 = 800`.
    2. De verpakkingsmachine laat een maximale hoogte van 12 centimeter toe. Bepaal de waarde van `x` bij `h = 12` cm. Geef de benadering in mm nauwkeurig.
    3. Is een nauwkeuriger benadering van `x` zinvol in deze situatie? Geef aan waarom.

  4. Vanaf een toren wordt een vuurpijl afgeschoten. De hoogte `h` van de vuurpijl hangt af van de tijd `t` dat deze onderweg is. Er geldt: `h = 100 + 40t - 5t^2`.
    Hierin is `h` in meter en `t` in seconden gemeten.
    1. Breng de grafiek van `h` in beeld op je grafische rekenmachine.
    2. Op welke hoogte boven de begane grond werd de vuurpijl afgeschoten? Na hoeveel seconden was de vuurpijl weer op diezelfde hoogte?
    3. Na hoeveel seconden was de vuurpijl op het hoogste punt in zijn baan? Hoeveel meter boven de begane grond was hij op dat moment?
    4. Na hoeveel seconden kwam de vuurpijl op de grond terecht?
    5. Kun je met deze gegevens de baan van de vuurpijl in beeld brengen? Verklaar je antwoord.

  5. De opbrengst `R` (in €) bij de verkoop van een bepaald artikel hangt af van het aantal stuks `q` dat je verkoopt en van de prijs `p` (in €) per stuk. In bepaalde economische omstandigheden hangt de verkochte hoeveelheid `q` af van de prijs `p` volgens de formule: `q = 4000 - 200p`.
    1. Bereken de opbrengst bij een prijs van € 2,50 per stuk.
    2. Bij welke prijs per stuk is er een opbrengst van € 18000,-?
    3. Laat zien dat er een maximale opbrengst is van € 20000,-.
    4. De verkoop van een bepaald product levert een zekere opbrengst op, maar brengt ook vaak kosten met zich mee. De winst is daardoor lager dan de opbrengst. Geef twee redenen waarom er kosten worden gemaakt. Geef ook een reden waarom die kosten van `q` af zullen hangen.
    5. Er is een verband tussen `R` en `q`. Stel een formule op die dat verband aangeeft.
    6. Voor de kosten `K` geldt: `K = 5000 + 15q`.
      Voor de winst `W` geldt: `W = R - K`.
      Stel een formule op voor de winst afhankelijk van `q` en bereken bij welke verkochte hoeveelheid de winst maximaal wordt.

Toepassen

  1. Koolmonoxide (CO) is één van de stoffen die via de uitlaat van een auto de lucht inkomt. De hoeveelheid CO die uitgestoten wordt is afhankelijk van de temperatuur van de motor en van de rijsnelheid.
    Voor de CO-uitstoot bij de warme motor geldt: `u = 4,4 + 196,0/v`.
    Bij een koude motor geldt: `u = 6,9 + 298,5/v`.
    Hierin is `u` de uitstoot in gram per kilometer en `v` de snelheid in kilometer per uur.
    1. Hoe kun je aan de formules zien dat de uitstoot afneemt als de snelheid toeneemt?
    2. De uitstoot van een koude motor bedroeg 14 g/km. Hoe hard reed deze auto?
    3. Iemand is geïnteresseerd in het verschil tussen de uitstoot bij een koude en bij een warme motor. Hij onderzoekt hoeveel procent de uitstoot bij een koude motor meer is dan bij een warme motor. Dat percentage hangt af van de snelheid. Hoe groot is dat percentage bij een snelheid van 30 kilometer per uur?
    4. Er bestaan ook formules waarbij de CO-uitstoot gegeven wordt afhankelijk van de ritlengte en de rijtijd. Voor een warme benzinemotor geldt: `u_(text{tot}) = 4,4L + 0,054T`.
      Hierin is `u_(text{tot})` de totale hoeveelheid CO in gram uitgestoten tijdens de rit, `L` de ritlengte in kilometers en `T` de rijtijd in seconden. Laat zien hoe deze formule kan ontstaan uit de eerste formule voor de CO-uitstoot bij een warme motor.

  2. Windmolens kunnen elektriciteit opwekken. Lees hierover:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Werken met formules > Totaalbeeld > Toepassingen

    Voor een zekere windmolen wordt dat aangegeven door de formule:
    `P = 0,00013 * v^3 * D^2`
    Hierin is `P` het (gemiddelde) vermogen in kW (kiloWatt), `v` de (gemiddelde) windsnelheid in m/s en `D` de rotordiameter in m.
    1. Ga uit van een windmolen met een diameter van 24 m. Bij welke windsnelheid in km/h wordt een vermogen van 26 kW opgewekt?
    2. Ga weer uit van een vermogen van 26 kW. Welke diameter de windmolen moet hebben, kun je dan nog berekenen. Stel een formule op die `D` uitdrukt in `v`.
    3. In een bepaald gebied ligt de windsnelheid tussen de 7,2 en de 36 km/h. Als je een (gemiddeld) vermogen van 26 kW met een windmolen wilt opwekken, tussen welke waarden kies je dan de diameter van die molen?

  3. Bij macro-economische modellen wordt de huishouding van een compleet land met meerdere formules en variabelen beschreven. Lees hierover:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Werken met formules > Totaalbeeld > Toepassingen

    De volgende vergelijkingen vormen zo'n macro-economisch model:

    EV = C + I + O
    C = 0,75 · (Y – B)
    I = 29
    O = 40
    B = 0,2 · Y + 12
    Y = EV

    Bij de variabelen EV, C, I, O, B en Y gaat het om miljarden guldens.
    De eerste vergelijking van het model noemen economen wel de definitievergelijking, want eigenlijk spreek je met die vergelijking alleen af wat je onder de effectieve vraag verstaat.
    De daarop volgende vier vergelijkingen heten de gedragsvergelijkingen.
    Die laten zien hoe voor een bepaalde economie C, I, O en B van het nationaal inkomen Y afhangen.
    In deze economie geven de particulieren bijvoorbeeld driekwart van het totale te besteden inkomen Y – B uit aan consumptiegoederen. De zesde vergelijking is de evenwichtsvoorwaarde: de vraag is even groot als het nationaal inkomen.
    Door deze zes vergelijkingen met elkaar te combineren kun je het nationaal inkomen van dit land uitrekenen en daarmee alle variabelen. Laat zien hoe dat gaat.

Examenopgaven

  1. Treinreizigers die op het station te U. uitstappen, kunnen de uitgang van het station alleen bereiken via een voetgangerstunnel. De tunnel is 30 meter lang en 3 meter breed. De snelheid van de voetgangersstroom in de tunnel is afhankelijk van de drukte. Een maat voor de drukte is de module, dat is het gemiddelde aantal vierkante meter per voetganger.
    1. Op zeker moment bevinden zich 120 mensen in de tunnel, die allen in de richting van de uitgang lopen. Bereken voor deze situatie de module.
    Het verband tussen de snelheid van de voetgangersstroom V en de module M wordt gegeven door de formule
    `V = 87 - 26/(M+0,5)`
    met `V` in meter per minuut en `M` in m2 per voetganger.
    1. Bereken de module bij een snelheid van 50 m per minuut. Geef je antwoord in twee decimalen nauwkeurig.
    2. Wanneer een voetganger ongehinderd kan lopen, is zijn snelheid ongeveer 5 km/h. Onderzoek of dat in overeenstemming is met de formule.
    3. Er bestaat een verband tussen de waarde van `M` en het aantal voetgangers dat per minuut de tunnel verlaat (`N`). Het verband tussen `M` en `N` staat grafisch weergegeven in de figuur. Schat zo nauwkeurig mogelijk hoeveel mensen er per minuut de tunnel verlaten in het geval dat de snelheid van de voetgangersstroom 70 m per minuut is.
    4. Een belangrijk gegeven bij het ontwerpen van een tunnel is het maximale aantal mensen dat in korte tijd kan worden verwerkt. Bij welke snelheid is het aantal voetgangers dat per minuut de tunnel verlaat maximaal? Licht je antwoord toe.

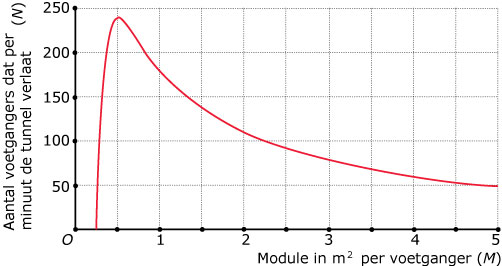
    (bron: examen wiskunde A havo 1989, tweede tijdvak)