Meerdere variabelen

Inleiding

Je ziet op veel plaatsen windmolens om elektriciteit op te wekken. Het vermogen (in kiloWatt) dat zo'n molen levert hangt af van de dubbele wieklengte D (in m) en van de windsnelheid v (in m/s). Het vermogen van een windmolen wordt gegeven door de formule:
P = 0,00013 · v³ · D².
Met je grafische rekenmachine kun je hierbij voor verschillende waarden van D grafieken maken van P als functie van v.

Je leert nu:

werken met formules met meer dan twee variabelen;
werken met grafiekenbundels en nomogrammen;
formules schakelen.

Je kunt al:

formules schrijven als functies en dan de grafieken goed in beeld brengen;
werken met technieken als terugrekenen, de balansmethode bij vergelijkingen en haakjes uitwerken.

Verkennen

Lees het verhaal van de windmolens uit de Inleiding.

> Maak grafieken van P als functie van v voor D = 10,20,30 meter
> In een bepaald gebied is de windsnelheid gemiddeld v = 5 m/s. Bij welke diameters levert deze windmolen een vermogen van tussen dan 10 kW en de 20 kW?
> Kun je daarbij je grafieken gebruiken?

Uitleg

Het vermogen van een windmolen wordt gegeven door de formule:
P = 0,00013 · v³ · D².
Dit is een formule met drie variabelen: het geleverde vermogen hangt zowel van de windsnelheid als van de grootte van de wieken af. Daarom kun je hierbij niet zo eenvoudig een grafiek maken.

Met je grafische rekenmachine kun je wel voor verschillende vaste waarden van D grafieken maken van P als functie van v.

Voor D = 10 krijg je P = 0,013v³.
Voor D = 20 krijg je P = 0,052v³.
Voor D = 30 krijg je P = 0,117v³.

En zo maak je een grafiekenbundel bij P als functie van v. Je kunt dan goed aflezen hoe het vermogen van de windsnelheid afhangt bij een bepaalde wieklengte.
Je kunt ook voor v een aantal vaste waarden kiezen en een grafiekenbundel maken bij P als functie van D. Dan kun je gemakkelijk aflezen welke diameter een molen moet hebben om bij een bepaalde gemiddelde windsnelheid een bepaald vermogen te leveren.

‡

Opgaven

Bekijk in de Uitleg de formule voor het vermogen van de windmolen nog eens.
1. Bereken het vermogen van een windmolen van dit type bij een rotordiameter van 12 m en een windsnelheid van 5 m/s.
2. Bij welke windsnelheid levert deze windmolen (rotordiameter 12 m) een vermogen van 7000 W?
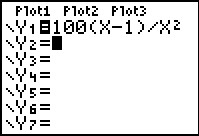
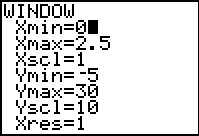
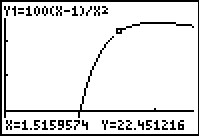
3. Als `D = 10` hangt `P` alleen van `v` af. Teken met je grafische rekenmachine een grafiek bij dit verband. Schrijf de ingevoerde formule en de vensterinstellingen op.
4. Maak ook grafieken van het verband tussen `P` en `v` voor `D = 10` en `D = 8`.

Bekijk in het practicum GR hoe je een bundel grafieken maakt op je grafische rekenmachine. Ga naar:
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Meerdere variabelen > Practicum GR
Maak de grafieken van opgave 1 als één grafiekenbundel op je GR.

Theorie

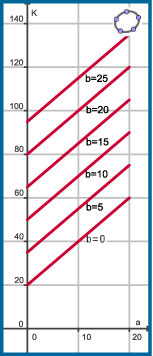
Een formule zoals K = 2a + 3b + 20 beschrijft een verband tussen drie variabelen.

Weet je twee van de drie variabelen, dan kun je de derde uitrekenen.
Als bijvoorbeeld a = 10 en b = 5, dan is K = 2 · 10 + 3 · 5 + 20 = 55.

Weet je één van de drie variabelen, dan blijft er een verband tussen de andere twee over. Als bijvoorbeeld b = 5, dan is K = 2a + 3 · 5 + 20 = 2a + 35.
Hierbij kun je een grafiek maken.
Kies je voor b een rijtje vaste waarden zoals b = 0,5,10,15,20,25 dan kun je een grafiekenbundel maken voor K als functie van a. Bij elke b-waarde hoort een nieuwe grafiek, dus je krijgt er zes in dit geval.

In toepassingen zoals rekenmodellen is vaak sprake van meerdere formules met meerdere variabelen. Soms kun je dan het aantal variabelen en het aantal formules terug brengen door een paar formules met elkaar te combineren. Zie voorbeeld 3.

‡

Voorbeeld 1

Een beroemde maat voor iemand's gezondheid is de Quetelet-index (QI) of tegenwoordig ook wel "body-mass-index" (BMI) genoemd. De QI is een maat voor het al of niet hebben van overgewicht. De formule ervoor is:
`QI=G/(l^2)`
waarin G het gewicht in kg en l de lengte in m is.
Je ziet hier een grafiekenbundel voor G als functie van l voor bepaalde waarden van de QI. Bij een QI vanaf 20 tot 25 heb je een normaal gewicht. Maak zelf deze grafiekenbundel op je GR.
Hoe zwaar weegt iemand van 1,75 m lengte met een normaal gewicht?

Antwoord

Om deze grafiekenbundel op je GR te maken moet je de waarden QI = 20,25,30 kiezen.
Bijvoorbeeld bij QI = 20 hoort `G/(l^2)=20` en dus G = 20 · l².
En zo vind je bij de andere waarden van QI de formules G = 25 · l² en G = 30 · l².
Deze drie formules voer je in.
Het venster loopt voor l (dus X) van 1,50 tot 2,00 en voor G (dus Y) van 0 tot 120.

Met de formules bepaal je dat iemand van 1,75 m lengte met een normaal gewicht tussen de 20 · 1,75² = 61,25 en 25 · 1,75² = 76,5625 kg weegt.

‡

Voorbeeld 2

In Voorbeeld 1 tref je de formule aan voor de Queteletindex `QI`.
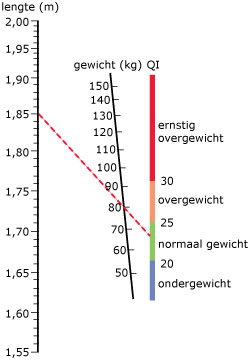
Je ziet hier een nomogram waarmee je de QI snel kunt bepalen. Welke QI heeft iemand van 1,85 m lengte met gewicht van 80 kg? Controleer de uitkomst met de formule.

Antwoord

Uit het nomogram lees je QI ≈ 23 af.

Met de formule: `QI = 80/(1,85^2) ~~ 23,4`.

Beide waarden stemmen goed overeen.
Controleer nog een paar waarden.

‡

Voorbeeld 3

Er zijn mensen die beweren dat je een gezond gewicht hebt als het voldoet aan de formule G = 100(l – 1). Laat zien dat in dit geval de QI inderdaad tussen de 20 en de 25 blijft voor normale lengtes.

Antwoord

Je kunt beide formules combineren door in de formule voor de QI de variabele G te vervangen door 100(l – 1). Je krijgt dan:

`QI = (100(l-1))/(l^2)`.

Van deze formule kun je met de grafische rekenmachine een grafiek maken.
Je zult dan zien dat voor lengtes tussen de 1,50 m en de 2,20 m de QI inderdaad tussen de 20 en de 25 ligt.

‡

Opgaven

Bekijk de formule voor het vetpercentage (de Queteletindex) in Voorbeeld 1 nog eens.
1. Over welke drie variabelen gaat deze formule?
2. Stel je voor dat `l = 1,95`. Welke formule geeft dan het verband tussen `QI` en `G`? Teken de grafiek van `QI` als functie van `G`.
3. Stel je voor dat `G=65`. Welke formule geeft dan het verband tussen `QI` en `l`? Teken de grafiek van `QI` als functie van `l`.
4. Stel je voor dat `QI=20`. Welke formule geeft dan het verband tussen `G` en `l`? Teken de grafiek van `G` als functie van `l`.

Gebruik weer de formule voor de Queteletindex.
1. Teken de grafiekenbundel van Voorbeeld 1 op je grafische rekenmachine.
2. Hoe zwaar weegt iemand van 1,90 m lengte met een normaal gewicht?

In Voorbeeld 2 zie je een zogenaamd nomogram bij de formule voor het vetpercentage.
1. Bepaal zo nauwkeurig mogelijk het vetpercentage van iemand met een lengte van 1,75 m die 75 kg weegt. Licht het antwoord toe.
2. Iemand met een lengte van 1,75 m heeft een gezond gewicht. Tussen welke twee waarden ligt dat gewicht?
3. Het hoogste vetpercentage dat iemand met een gezond gewicht kan hebben is 25. Maak een tabel en een grafiek van de mogelijke gewichten afhankelijk van de lengte. Lees daartoe het gewicht af bij lengtes van 1,60, 1,70, 1,80, 1,90 en 2,00 meter.
4. Hoe kun je de grafiek bij c controleren met je grafische rekenmachine?

Je kunt nu zien wanneer iemand valt in één van de categorieën 'ondergewicht', 'normaal gewicht', 'overgewicht' en 'ernstig overgewicht'. Teken zelf op roosterpapier een grafiekenbundel bij de formule van de Queteletindex en geef daarin deze vier categoriën aan.

Bekijk in Voorbeeld 3 hoe je de formule voor een gezond gewicht en die voor de Queteletindex met elkaar kunt combineren.
1. Maak zelf de grafiek van de `QI` van iemand met een gezond gewicht als functie van `l`.
2. Ga na dat voor lengtes tussen de 1,50 m en de 2,20 m de `QI` inderdaad tussen de 20 en de 25 ligt.

Verwerken

Het vermogen van een windmolen wordt gegeven door de formule:
P = 0,00013 · v³ · D².
Voor een bepaalde waarde van `D` (de rotordiameter) vind je een verband tussen `P` en `v`.
1. Teken op roosterpapier een grafiekenbundel bij `D = 5`, `D = 10`, `D = 15` en `D = 20` meter. Ga er van uit dat `0 <= v <= 40`.
2. Lees in de grafiekenbundel de waarde van `P` af als `v = 8` en `D = 10`. Omschrijf hoe je dat doet. Controleer je antwoord met de formule.
3. In de grafiekenbundel kun je zien hoe het vermogen bij een bepaalde diameter afhangt van de windsnelheid. Arceer het gebied waarvoor geldt: de diameter ligt tussen de 10 en de 20 meter en de windsnelheid is maximaal 90 km/h.
4. Hoeveel bedraagt nu het maximale vermogen dat kan worden opgewekt?

Een gemeente wil het water in haar buitenzwembad op 20°C houden. Dit hoopt men te bereiken door een verwarmingsinstallatie aan te leggen. Omdat je in de zomermaanden ook van de zonnewarmte kunt profiteren, voorspelt een verwarmingsdeskundige dat de verwarmingskosten `k` zullen voldoen aan de formule: `k = 800-60u-50t`, waarin `u` het gemiddelde aantal zonne-uren per dag is en `t` het aantal graden Celsius is dat de buitentemperatuur afwijkt van de 20°C. `k` wordt gerekend in € per dag.
1. Welke betekenis heeft het getal 800 in deze formule?
2. Op een bepaalde dag is de gemiddelde temperatuur 16°C. Dan is `t = -4`. Als er die dag 3,5 zonne-uren zijn, hoe groot zijn dan de verwarmingskosten?
3. Onder welke omstandigheden blijft de temperatuur van het zwembad kostenloos op 20°C? Beschrijf een paar mogelijke situaties.
4. Teken op roosterpapier een grafiekenbundel voor `k` afhankelijk van `u` voor `t = -2`, `t = -1`, `t = 0`, `t = 1` en `t = 2`.
5. Geef in je grafiekenbundel aan hoe hoog de verwarmingskosten zijn als op een bepaalde dag de zon 6 uur schijnt en de temperatuur 22°C bedraagt. Bereken dit antwoord ook met de formule.
6. In een bepaalde week varieert de temperatuur tussen de 18°C en de 22°C. Het aantal uren zon per dag varieert van 4 uur tot maximaal 10 uur. Tussen welke twee bedragen liggen de totale verwarmingskosten voor het zwembad in die week?

De ANWB adviseert om bij het autorijden een afstand `d` (in m) te bewaren die de helft is van je eigen snelheid `v` in km/h.
1. Geef de formule van `d` als functie van `v`.
Gemiddeld is een auto 4 m lang. De afstand tussen de voorbumpers van twee auto's is dus `s=4+d` m. Neem aan dat alle auto's zich aan het advies van de ANWB houden, 4 m lang zijn en dezelfde snelheid `v` hebben.
1. De tijd `t` in seconden tussen twee auto's is nu te berekenen met de formule: `t=(3,6s)/v`.
  Licht dit toe.
2. Stel een formule op voor `t` als functie van `v` door formules te combineren.
3. Het aantal auto's `N` dat per minuut een bepaald punt passeert is: `N=60/t`.
  Schrijf de formule op van `N` als functie van `v`.
4. Er passeren 29,9 auto's per minuut. Hoe groot is de snelheid `v` van deze autostroom?

Hoeveel brandstof een personenauto verbruikt, hangt onder andere af van de af te leggen afstand, de rijstijl en het wachten voor verkeerslichten. We gaan dit met behulp van een wiskundig model nader onderzoeken. In dit model wordt het brandstofverbruik `B` (in mL) van een auto berekend met de volgende formule:
`B = a * L + b * S + c * D`
met:
- `L` = ritlengte in km;
- `S` = aantal stops onderweg;
- `D` = totale wachttijd voor verkeerslichten in seconden.
`a` en `b` zijn getallen die van de rijsnelheid `V` (in km/h) afhangen en `c` is een constante. Voor `a`, `b` en `c` geldt:
`a = 170 - 4,55V + 0,049V^2`
`b = 0,0077V^2`
`c = 0,39`
We laten in dit model optrekken en afremmen buiten beschouwing, zodat we in de uitdrukkingen voor `a` en `b` steeds een constante waarde voor `V` kunnen invullen.
1. Neem een rit over 1 km met een snelheid van 50 km/h, 2 stops onderweg en een totale wachttijd van 40 seconden. Bereken hoeveel procent van het totale brandstofverbruik gebruikt wordt voor de stops en het wachten.
Twee auto’s staan voor verkeerslicht `P`. 600 m verderop staat een verkeerslicht `Q`. Als de auto’s tussen `P` en `Q` met een snelheid van 50 km/h rijden, springt het verkeerslicht `Q` precies op tijd op groen en kunnen ze doorrijden. Houd geen rekening met afremmen en versnellen.
Auto 1 rijdt tussen `P` en `Q` steeds met een snelheid van 50 km/h en kan dus doorrijden bij `Q`. Auto 2 rijdt met een snelheid van 70 km/h, zodat deze zal moeten stoppen en wachten bij Q.
1. Laat met een berekening zien dat auto 2 ruim 12 seconden voor verkeerslicht `Q` moet wachten.
2. Bekijk de eerste 900 m na verkeerslicht `P`. Na `Q` komt er geen verkeerslicht meer en auto 1 rijdt ook daar 50 km/h en auto 2 rijdt daar weer 70 km/h. Onderzoek of auto 2 meer dan twee keer zo veel brandstof nodig heeft als auto 1.

Testen

Bij de verkoop van een bepaald artikel gelden de formules `TO = p * q` en `q = 200 - 0,5p`, waarin `TO` de totale maandelijkse opbrengst bij de verkoop van dat artikel is. `p` is de prijs (in €) en `q` is de verkochte hoeveelheid per maand.
1. Combineer deze twee formules tot een formule voor `TO` als functie van `q`.
2. Voor de maandelijkse winst `TW` geldt: `TW=TO-TK` waarin `TK=40q` de totale maandelijkse kosten voor dit artikel zijn. Stel een formule op voor `TW`.
3. Bij welke verkoopcijfers wordt winst gemaakt?

Het subsidiebedrag `B` dat een sportclub jaarlijks ontvangt hangt af van het aantal seniorleden `s` en het aantal junioren `j`. Er geldt: `B=1000+10j+5s`.
1. Hoeveel subsidie krijgt een sportclub met 60 junioren en 115 senioren?
2. Maak op roosterpapier bij deze formule een grafiekenbundel met `B=1000`, `B=1500`, `B=2000`, `B=2500`.
3. In een bepaald jaar ontvangt men een subsidie van 1600 euro. Er zijn dat jaar 80 senioren. Geef in je grafiek aan hoeveel junioren de club dat jaar heeft. Bereken dit aantal met de formule.
4. Al jaren lang ontvangt men een subsidie van tussen de 1500 en de 1800 euro. Geef in je grafiek het bijbehorende gebied aan.
5. Het aantal seniorleden blijft ook al jaren constant, ongeveer 80 personen. Tussen welke aantal heeft het aantal juniorleden dan gevarieerd? Geef dit in de figuur aan.