Ongelijkheden

Inleiding

Als wilt weten bij welke windsnelheid een windmolen meer dan bijvoorbeeld 20 kW aan vermogen levert, dan moet je een ongelijkheid oplossen. Hetzelfde geldt als je wilt weten vanaf hoeveel gereden km per jaar een auto op benzine duurder is dan één op diesel. Of hoeveel uur de éne kaars langer is dan de andere. Over het oplossen van ongelijkheden gaat dit onderdeel.

Je leert nu:

ongelijkheden systematisch oplossen.

Je kunt al:

formules schrijven als functies en dan de grafieken goed in beeld brengen;
werken met technieken als terugrekenen, de balansmethode bij vergelijkingen en haakjes uitwerken.

Verkennen

Kaars I is 25 cm lang en brandt in 8 uur tijd volledig op. Kaars II is 20 cm lang en brandt in 10 uur volledig op. Beide kaarsen branden gelijkmatig, per uur brandt er steeds een vast aantal cm op.

> Hoe lang (in minuten nauwkeurig) is kaars I langer dan kaars II?

Uitleg

Bekijk het probleem bij Verkennen nog eens.
De gestelde vraag kun je oplossen met je grafische rekenmachine.
Je maakt dan eerst formules van de lengte L (in cm) van elke kaars afhankelijk van de tijd t in uren.

Kaars I: in 8 uur is er 25 cm opgebrand, dus 25/8 = 3,125 cm/uur.
De bijpassende formule is L_I = 25 – 3,125t.
Kaars II: in 10 uur is er 20 cm opgebrand, dus 20/10 = 2 cm/uur.
De bijpassende formule is L_II = 20 – 2t.

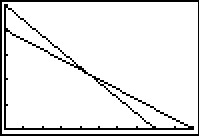Even een paar nette grafieken maken (de vensterinstellingen volgen meteen uit het kaarsenverhaal).
Het snijpunt van beide grafieken laat je de machine bepalen, je vindt t ≈ 4,44.
Kaars I is langer vanaf t = 0 tot en met t = 4,44 uur.
Dat is iets minder dan 4 uur en 27 minuten.

‡

Opgaven

In de Uitleg zie je de vraag hoe lang kaars I langer is dan kaars II wordt opgelost.
Daarbij wordt de grafische rekenmachine gebruikt.
1. Leg uit dat hier wordt opgelost `25 – 3,125t > 20-2t`.
2. Voor het snijpunt van de twee grafieken wordt de GR gebruikt. Nodig is dat niet. De vergelijking `25 – 3,125t = 20-2t` kun je met de balansmethode oplossen. Laat zien dat je dan dezelfde oplossing vindt.
3. Je vindt `t~~4,44`. Hoe bereken je dan dat kaars I 4 uur en 27 minuten langer is dan kaars II?

Bekijk de voorgaande opgave.
Kaars III is 30 cm lang en brandt in 6 uur tijd volledig op.
Hoe lang is kaars III de langste kaars?

Theorie

Een vraag als: "Voor welke x is 6 – x > 0,5x?" is een voorbeeld van een ongelijkheid.

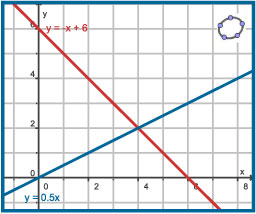Zo'n ongelijkheid los je op door in één figuur de grafieken te tekenen van y₁ = 6 – x en y₂ = 0,5x.
Je ziet dat voor x = 4 geldt dat y₁ = y₂, dat voor x < 4 geldt dat y₁ > y₂ en dat voor x > 4 geldt dat y₁ < y₂.

Het antwoord op de vraag, de oplossing van de ongelijkheid, is daarom x < 4.

Op dezelfde wijze kun je ook werken met ongelijkheden waarin het gaat om "kleiner dan" (<), "kleiner of gelijk aan" (`<=`) en "groter of gelijk aan" (`>=`).

‡

Voorbeeld 1

Een verfhandelaar heeft een mengmachine van € 2000,00. De inkoopprijs van de verf en het kosten van het mengproces samen komt op € 5,00 per liter. Hij verkoopt zijn verf voor € 7,25 per liter.
Hij maakt winst als de opbrengst TO groter is dan de totale kosten TK. Met voorraadkosten wordt geen rekening gehouden.
Bereken algebraïsch vanaf hoeveel liter verkochte verf hij winst gaat maken.

Antwoord

Er geldt: TK = 2000 + 5q en TO = 7,25q.
Hierin is q de verkochte hoeveelheid verf.

Nu moet: TO > TK, dus 7,25q > 2000 + 5q.
Met de grafische rekenmachine breng je de grafieken van TO en TK goed in beeld. (Het snijpunt moet zichtbaar zijn.) Vervolgens bereken je dit snijpunt: q ≈ 888,9 liter.

De oplossing lees je uit de grafiek af: `q >= 888,9`, dus vanaf 888,9 L verf.

‡

Voorbeeld 2

Je ziet op veel plaatsen windmolens om elektriciteit op te wekken. Het vermogen dat zo’n molen levert hangt af van de wieklengte en van de windsnelheid v.

Het vermogen van een zekere windmolen wordt gegeven door: P = 0,052v³.
Hierin is P het (gemiddelde) vermogen in kW (kiloWatt), v de (gemiddelde) windsnelheid in m/s en de diameter van de cirkel die de uiterste punt van een wiek maakt bij het draaien is 20 meter.
Bereken vanaf welke windsnelheid het vermogen van de windmolen meer dan 20 kW bedraagt.

Antwoord

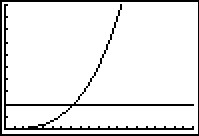
Het oplossen van zo’n ongelijkheid gaat met je grafische rekenmachine:

Je voert Y1=0.052X^3 en Y2=20 in en brengt ze goed in beeld.

Je bepaalt het snijpunt van beide grafieken: (7,27;20).

Je leest de oplossing van de ongelijkheid uit de figuur af: v > 7,27.

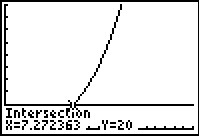Belangrijk is nog het aantal decimalen waarop je moet afronden. Het gegeven antwoord is op twee decimalen nauwkeurig juist. Moet je echter op één decimaal nauwkeurig afronden, dan is het antwoord: `v >= 7,3`.
Want bij 7,3 is het vermogen al meer dan 20 kW.

‡

Voorbeeld 3

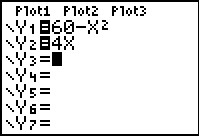
Los op: `60 - x^2 >= 4x`.

Antwoord

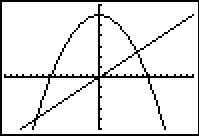
Je bekijkt eerst de grafieken van y₁ = 60 – x² en y₂ = 4x. Bij de meeste waarden van x zijn de functiewaarden verschillend.
Alleen bij de snijpunten zijn de functiewaarden gelijk.

De snijpunten vind je door op te lossen:
60 – x² = 4x.
Je vindt met de GR: x = –10 V x = 6.

Lees nu uit de figuur af, dat de oplossing van de ongelijkheid is: `-10 <= x <= 6`.

‡

Opgaven

In Voorbeeld 1 zie je hoe je de ongelijkheid `7,25q > 2000 + 5q` oplost met de grafische rekenmachine.
Je gaat de ongelijkheid `7,25q <= 2000 + 5q` zelf algebraïsch oplossen.
1. Los de vergelijking `7,25q = 2000 + 5q` algebraïsch op.
2. Schrijf de juiste oplossing van de ongelijkheid op.

In Voorbeeld 2 zie je hoe de ongelijkheid `0,052v^3 > 20` wordt opgelost.
Daarbij wordt de grafische rekenmachine gebruikt.
1. Voer deze oplossing zelf uit.
Bij een algebraïsche aanpak bereken je eerst de oplossingen van de vergelijking `0,052v^3 = 20` met behulp van terugrekenen.
1. Laat zien dat je dan dezelfde oplossing vindt.
2. Wat is het voordeel van een algebraïsche aanpak?

Stel je voor dat je al jaren in een auto op benzine rijdt. De benzineprijs blijft echter maar stijgen en je vraagt je af of je niet beter een gastank kunt laten inbouwen en op gas gaan rijden. Nu zijn je kosten per kilometer ongeveer 12,5 cent aan benzine.
1. Stel een formule op voor de benzinekosten per jaar (`B` in euro) afhankelijk van het aantal gereden kilometers (`a`).
2. Een gastank kost (inclusief inbouwen) € 1250,00. Je kosten per kilometer gaan omlaag, want gas kost 80 cent per liter en je rijdt 10 kilometer op 1 liter gas. Je wilt de gastank in één jaar terugverdienen. Stel een formule op voor de kosten in het eerste jaar dat je op gas rijdt (`G`) afhankelijk van het aantal kilometer (`a`).
3. Je wilt weten hoeveel kilometer je in dat jaar moet rijden om de gastank er weer uit te hebben. Welke ongelijkheid hoort daar bij?
4. Los deze ongelijkheid algebraïsch op met `a` in km nauwkeurig.

Bekijk in Voorbeeld 3 hoe je de ongelijkheid `60-x^2 >= 4x` oplost.
1. Los zelf deze ongelijkheid met de grafische rekenmachine op. Zorg voor de juiste vensterinstellingen!
2. Welke oplossing heeft de ongelijkheid `60-x^2 < 4x`? (Hij bestaat uit twee delen.)

Verwerken

Los de volgende ongelijkheden algebraïsch op.
1. `10-2x > 4x+8`
2. `60-x^2 <= -4`
3. `600+0,05x > 800+0,025x`

Los deze ongelijkheid met de grafische rekenmachine op: `x^2-x>90`.

Je rijdt al een Smart Fortwo voor € 5,00 per dag! Stel je hebt op 1 januari 2006 een Smart gekocht en betaalt die 5 euro per dag. Daarnaast heb je onderhoudskosten: voor 1,5 cent per gereden kilometer kun je daarvoor een abonnement afsluiten waar vrijwel alle onderhoudskosten mee worden afgedekt. Je hebt dan dus alleen nog benzinekosten. Je kunt met 1 liter benzine 15 kilometer rijden en 1 liter benzine kost ongeveer € 1,50.
1. Hoeveel cent per kilometer ben je kwijt aan benzine en onderhoud samen?
2. Hoeveel kost je deze Smart per jaar als je er 16000 km/h mee rijdt?
3. Stel een ongelijkheid op bij de vraag: Hoeveel kilometer per jaar mag je maximaal met deze Smart rijden als je minder dan € 4000,00 kwijt wilt zijn dat jaar? Los daarna die ongelijkheid algebraïsch op.
4. Eigenlijk geldt het onderhoudsabonnement van 1,5 cent per gereden kilometer pas vanaf 15000 km/jaar. Rijd je minder, dan betaal je alsof je 15000 km/jaar rijdt. Stel het complete functievoorschrift op voor de jaarlijkse kosten `K` als functie van het aantal gereden kilometers.

Twee auto’s rijden op de A1, beide met een (ongeveer) constante snelheid. Bestuurder A houdt een snelheid van 110 km/h aan. Bestuurder B rijdt met 120 km/h . Als bestuurder B bij de IJsselbrug bij Deventer komt ligt hij 24 kilometer achter op bestuurder A. Het tijdstip waarop dat gebeurt is `t = 0`. De afstand (in kilometers) tot Deventer wordt voorgesteld door `a`.
1. Stel bij beide auto’s een formule voor `a` als functie van `t` op.
2. Bereken na hoeveel minuten auto A door B wordt ingehaald.
3. Bereken algebraïsch hoe lang hun onderlinge afstand minder dan 4 kilometer is.

Testen

Los de volgende ongelijkheden algebraïsch op.
1. `6-x < 4x-3`
2. `10/x>=0,25`
3. `(2x-6)^2<16`

Los deze ongelijkheid op (in twee decimalen nauwkeurig) met de grafische rekenmachine: `x^3 > 6-x`.

De afstand Utrecht - Enschedé is voor een fietser 144 kilometer.
Fietser A gaat met 18 km/h van Utrecht naar Enschedé.
Fietser B gaat met 24 km/h van Enschedé naar Utrecht.
Beide fietsers starten tegelijkertijd.
1. Je wilt weten hoe lang fietser A dichter bij Utrecht is dan fietser B.
  Welke ongelijkheid hoort daar bij als `t` de tijd in uren is?
2. Los deze ongelijkheid algebraïsch op.
3. Beantwoord de vraag in minuten nauwkeurig.