
Vergelijkingen
Inleiding
Een architect wil een goede trap ontwerpen. Hij gebruikt daarvoor de formule:
2 · optrede + aantrede = paslengte
Hij gaat uit van een paslengte van 70 cm.
Voor de optrede wil hij 16 cm nemen.
Vult hij deze gegevens in de formule in, dan krijgt hij de vergelijking: 32 + aantrede = 70.
Hij kan dus als aantrede nemen: aantrede = 70 – 32 = 38 cm.
Op deze manier heeft hij de vergelijking opgelost.
Het getal 38 maakt de vergelijking kloppend: 32 + 38 = 70.
Je leert nu:
- systematisch vergelijkingen oplossen met en soms zonder de grafische rekenmachine.
Je kunt al:
- formules schrijven als functies;
- werken met technieken als terugrekenen, de balansmethode bij vergelijkingen en haakjes uitwerken.
Verkennen
De huurprijs van een kopieerapparaat bedraagt € 250,00 per maand.
Het maken van een kopie kost € 0,06. Op school staat zo’n apparaat speciaal
voor gebruik door leerlingen. De leerlingen betalen € 0,10 per kopie.
> Bij welk aantal kopieën per maand speelt de school quitte?
> Heb je deze vraag opgelost met een vergelijking? Zo nee, welke vergelijking zou dat dan moeten zijn?
Uitleg
Bekijk het probleem bij Verkennen nog eens.
De vraag: "Bij welk aantal kopieën per maand speelt de school quitte?" kun je vertalen naar een vergelijking:
- Noem het aantal kopieën per maand a.
- De kosten voor de school bedragen dan maandelijks 250 + 0,06 · a euro.
- De opbrengst van de school is maandelijks 0,10 · a euro.
Ze spelen quitte als 250 + 0,06 · a = 0,10 · a.
Dit is een typisch voorbeeld van een vergelijking: je vergelijkt kosten en opbrengst en vraagt je af waar beide gelijk zijn.
In dit geval kun je de vergelijking oplossen met de balansmethode. Ga na dat je vindt: a = 6250.
‡
Opgaven
-
Het probleem bij Verkennen wordt in de Uitleg opgelost.
-
Welke vergelijking wordt daartoe opgesteld?
-
Laat zien hoe je deze vergelijking met de balansmethode oplost.
-
Doe nu het vervolg van het practicum "Functies met de GR" via
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Vergelijkingen > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Vergelijkingen > Practicum
Bekijk goed hoe je de rekenmachine een vergelijking voor je kan oplossen door snijpunten van grafieken te bepalen.
Los vervolgens de vergelijking van opgave 1 op met behulp van de grafische rekenmachine.
Theorie
Elke wiskundige zin met een is-gelijk-teken is een vergelijking, bijvoorbeeld:
- Voor een rechthoek met lengte l, breedte b en een omtrek van 100 geldt 2l + 2b = 100.
- Voor een vierkant met oppervlakte A en zijde z geldt: A = z2.
- Voor het aantal kopieën a per maand geldt 250 + 0,06 · a = 0,10 · a.
- Een getal en zijn kwadraat zijn samen 90, hoeveel bedraagt dat getal?
Vergelijkingen zoals de eerste twee beschrijven het verband tussen twee variabelen.
Daarbij maak je vaak een grafiek.
In de laatste twee gevallen kun je de vergelijking oplossen.
Dat betekent een waarde voor de onbekende zoeken die de gegeven zin, de gegeven vergelijking waar maakt.
Daarvoor bestaan verschillende technieken, zoals de balansmethode en de terugrekenmethode. In de voorbeelden zie je nog eens hoe die methoden in zijn werk gaan.
Je kunt vergelijkingen ook goed door je grafische rekenmachine laten oplossen, zie voorbeelden 3 en 4.
‡
Voorbeeld 1
Los de vergelijking `1/2 (x+8) = -7+x` op met de balansmethode.
Antwoord
Haakjes uitwerken: `1/2 x+4 = -7+x` beide zijden –4
`1/2 x = -11 + x` beide zijden –x
`-1/2 x = -11` beide zijden vermenigvuldigen met –2
`x=22`
Je kunt dit antwoord nog controleren door aan beide zijden van de gegeven vergelijking voor x het getal 22 te substitueren.
‡
Voorbeeld 2
In de vergelijking 2(x – 4)2 = 32 komt de onbekende x maar op één plek voor. Je kunt hem oplossen met terugrekenen.
Antwoord
Eerst even uitzoeken hoe je heen rekent vanuit x:
x  32
32
Vervolgens ga je terugrekenen:
x 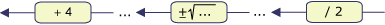 32
32
Je vindt: `x=+-sqrt(32/2)+4` en dus x = 0 V x = 8
En weer controleren door invullen!
‡
Voorbeeld 3
De vergelijking `x+x^2=10` kun je oplossen met de grafische rekenmachine.
Hij heeft daar een ingebouwde routine voor.
Antwoord
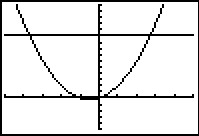
Eerst maak je de grafieken van y1 = x + x2 en y2 = 10 op de grafische rekenmachine. Breng ze zo in beeld dat alle snijpunten zichtbaar zijn!
De grafieken snijden elkaar tweemaal. De vergelijking heeft twee oplossingen.
Vervolgens heeft de grafische rekenmachine een routine om de snijpunten van twee grafieken te berekenen. In het practicum kun je zien hoe dit gaat.
Je laat de grafische rekenmachine eerst het éne snijpunt berekenen. Op dezelfde manier bepaal je vervolgens het andere snijpunt.
Op twee decimalen nauwkeurig is de volledige oplossing: x ≈ 2,70 of x ≈ –3,70.
‡
Voorbeeld 4
Als je 360 meter afrastering beschikbaar hebt voor een rechthoekig veld met een oppervlakte van 0,5 hectare dan geldt:
l · b = 5000 en 2l + 2b = 360
als je voor de lengte (in m) de variabele l en voor de breedte (in m) de variabele b kiest.
Zoek nu waarden voor l en b die aan beide formules voldoen.
Antwoord
Schrijf de formules als: `l=5000/b` en l = 180 – b.
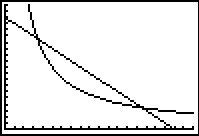
Voer je ze in de grafische rekenmachine in als Y1=5000/X en Y2=180-X.
Om een goede grafiek te krijgen kies je verstandige grenzen van de waarden van X (de breedte)
en Y (de lengte).
Je ziet dat de grafieken twee snijpunten hebben.
In die punten geldt de vergelijking: `5000/b=180-b`.
Je kunt de snijpunten met je grafische rekenmachine vinden. De gevonden X-waarden zijn de oplossingen van de vergelijkingen, de waarden van b die hem waar maken.
‡
Opgaven
-
Bekijk Voorbeeld 1.
Los de volgende vergelijkingen op met de balansmethode.
-
`3t - 400 = 700`
-
`3t - 400 = 700 - 2t`
-
`2300 - 0,15 * p = 1600 + 0,42 * p`
-
Bekijk Voorbeeld 2.
Los de volgende vergelijkingen op door terugrekenen.
-
`3t - 400 = 700`
-
`(3 * t - 20)^2 = 1600`
-
`3 * p^3 = 81`
-
Niet alle vergelijkingen kun je met de balansmethode of door terugrekenen systematisch oplossen. In Voorbeeld 3 kun je nalezen hoe je met de grafische rekenmachine vergelijkingen oplost.
Los de volgende vergelijkingen op met de GR. Geef je oplossingen in drie decimalen nauwkeurig.
-
`x^3 = 4 - x`.
-
`600/a = 18 + 0,04a`
-
Los de volgende vergelijkingen op met de grafische rekenmachine. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
-
`x^3 + 2x = 16`
-
`x + sqrt(x) = 10`
-
`l + 10/l = 10`
-
`300/(p+4)=20`
-
Bekijk in Voorbeeld 4 hoe je vanuit twee gegevens formules één vergelijking afleidt.
Die vergelijking los je vervolgens op.
-
Voer de twee functies in de grafische rekenmachine in.
-
Laat nu de GR de snijpunten van beide grafieken bepalen.
-
Wat wordt de oplossing van je vergelijking?
Verwerken
-
Los de volgende vergelijkingen algebraïsch op.
-
`4t + 50 = 200`
-
`4t^2 + 50 = 200`
-
`6p-20=12+4p`
-
`x^2+4=20`
-
`(x-5)^2=4`
-
`4(a-2)-20=0`
-
`12/V=400`
-
`2x^2-2=6x^2+14`
-
Los de volgende vergelijkingen op door inklemmen met behulp van je grafische rekenmachine. Zoek alle oplossingen.
-
`sqrt(x)=6-x`
-
`x^4=2+x`
-
Voor het verbruik van water moet je een vast bedrag per jaar betalen. Dat heet
vastrecht. Verder betaal je per verbruikte m3 een vaste prijs. Een waterleidingbedrijf
heeft voor dit jaar die bedragen zo vastgesteld:
- vastrecht: € 38,-
- prijs per m3: € 1,75
De totale jaarlijkse kosten `TK` voor het waterverbruik hangen dus af van het aantal m3 (`a`) dat verbruikt is.
-
Verklaar waarom geldt: `TK = 38 + 1,75a`.
-
Het waterleidingbedrijf schat dat een bepaald gezin dit jaar tussen de 140 en de 160 m3 water zal verbruiken.
Geef aan tussen welke waarden de kosten voor het gezin in een jaar zullen liggen.
-
Het gezin wil de kosten voor waterverbruik per jaar terugbrengen tot onder de € 250,-.
Hoeveel water mogen ze dan maximaal verbruiken?
-
Bereken bij deze formules de waarde van de éne variabele als de andere 0 is.
-
`2p - 3q = 600`
-
`W = -0,25q(0,5q - 100)`
-
`k^2 + (l + 2)^2 = 100`
-
`a = 1200/(600+0,2d)`
-
Sommige kaarsen zijn bijna zuiver cilindervormig. Stel je voor dat je zo’n kaars wilt maken met een lengte van 20 cm. Je neemt een lont met een diameter van 3 mm en dompelt die een aantal keer in een bad met vloeibaar kaarsvet. Elke onderdompeling wordt de diameter van de kaars 1 mm groter. De hoeveelheid kaarsvet `V` in de kaars hangt af van het aantal onderdompelingen `a`.
-
Geef een formule voor `V` als functie van `a`.
-
Breng de grafiek van deze functie met je grafische rekenmachine in beeld.
-
Na hoeveel onderdompelingen is de hoeveelheid kaarsvet in de kaars ongeveer 106 cm3?
Lees je antwoord eerst uit de grafiek af en bereken het daarna door de bijbehorende vergelijking algebraïsch op te lossen.
Testen
-
Los de volgende vergelijkingen algebraïsch op.
-
`1,25t + 5,50 = 1,85t`
-
`0,15(p - 2)^2 = 1,35`
-
`12 - x^2 = 0`
-
`600*g^2 = 5000`
-
Los de volgende vergelijking op door inklemmen met behulp van je grafische rekenmachine.
(Eventuele benaderingen in één decimaal nauwkeurig.)
`0,12q + 600/q = 30`
-
Voor de totale oppervlakte `A` van een cilindervormig groenteblik met straal `r` en hoogte `h` geldt: `A = 2pi r^2 + 2pi rh`.
-
Leg uit hoe je deze formule zelf kunt afleiden.
-
Bereken in cm3 nauwkeurig de oppervlakte van een groenteblik met een diameter van 20 cm en een hoogte van 30 cm.
-
Een groenteblik met een oppervlakte van 1000 cm2 heeft een hoogte van 20 cm. Bereken de diameter in mm nauwkeurig.
-
Van een groenteblik met een oppervlakte van 1000 cm2 zijn de hoogte en de diameter even groot.
Bereken de diameter in mm nauwkeurig.
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Vergelijkingen > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Vergelijkingen > Practicum

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Vergelijkingen > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Vergelijkingen > Practicum
 32
32
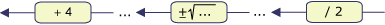 32
32

