
Grafieken maken
Inleiding
Een grafische rekenmachine is erg handig als je grafieken van functies wilt bekijken.
Maar er is één probleem: hoe krijg je de grafiek goed in beeld?
Je weet wel dat je de instellingen van het venster kunt aanpassen (toch?), maar dan moet je wel weten welke instellingen handig zijn. En dat moet je proberen te achterhalen uit de situatie waarbinnen je de formule gebruikt. Zowel je invoerwaarden als je uitkomsten moeten redelijk zijn...
Je leert nu:
- grafieken goed in beeld krijgen op je grafische rekenmachine;
- de karakteristieken van functies herkennen en vinden met behulp van de grafische rekenmachine.
Je kunt al:
- grafieken maken op de grafische rekenmachine;
- formules herschrijven tot ze als functie kunnen worden ingevoerd.
Verkennen
De huurprijs van een kopieerapparaat bedraagt € 250,00 per maand.
Het maken van een kopie kost € 0,06. Op school staat zo’n apparaat speciaal
voor gebruik door leerlingen. De leerlingen betalen € 0,10 per kopie.
> Geef een formule voor de prijs per kopie (P) als functie van het aantal kopieën (a).
> Maak een goede grafiek van deze functie.
> Welke uitkomsten krijg je als a heel groot wordt?
> En bij welke waarde van a maakt de school winst?
Uitleg
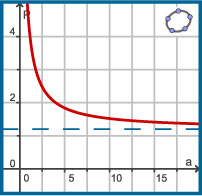
Voor een rit in een taxi betaal je:
-
voorrijkosten € 3,20
-
per gereden kilometer € 1,20
De prijs P per gereden km hangt af van het aantal gereden km a.
Er geldt: `P=1,20+(3,20)/a`.
De grafiek van deze functie heeft geen nulpunten, of extremen, maar wel geldt:
- Als a (het aantal gereden kilometers) heel groot wordt, benaderen de functiewaarden het getal 1,20. Je ziet dat als je een tabel bij de functie maakt.
Dit betekent dat de grafiek steeds dichter bij de lijn P = 1,20 komt te liggen. Deze lijn heet de horizontale asymptoot van de grafiek van P.
- Als a dicht bij 0 komt, worden de functiewaarden steeds groter: P(0,1) = 33,20; P(0,01) = 321,20; P(0,001) = 3201,20; P(0,0001) = 32001,20; etc.
Het getal 0 zelf mag je echter niet voor a invullen: delen door 0 levert geen reëel getal op.
Dit betekent dat de grafiek steeds dichter bij de lijn a = 0 (de verticale as) komt te liggen. Dit is de verticale asymptoot van de grafiek van P.
Als je de grafiek van de functie tekent, zorg je er voor dat ook
dit soort karakteristieke gedrag zichtbaar wordt.
‡
Opgaven
-
Bekijk de Uitleg en vooral het begrip asymptoot.
Van een bepaald type kopieerapparaat worden de maandelijkse kosten per kopie gegeven door `K = 200/a + 0,075`.
Hierin is `a` het aantal kopieën per maand en `K` zijn de kosten in euro.
-
Bereken de kosten per kopie als er 10000 kopieën per maand met deze machine worden gemaakt.
-
Welke waarde benaderen de kosten per kopie als het aantal kopieën heel erg groot is?
-
Welke horizontale asymptoot heeft de grafiek van `K`?
-
Als er een bepaalde maand geen kopieën worden gemaakt, kun je niet spreken van de kosten per kopie.
Het minimale aantal kopieën waarbij dit nog wel kan is 1. Hoeveel bedragen de kosten per kopie maximaal?
Theorie
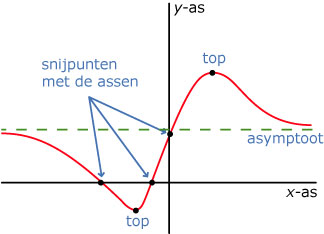
Als je de grafiek van een functie goed in beeld hebt, zijn alle karakteristieken zichtbaar (op het gewenste domein). Dat zijn:
-
de snijpunten met de assen, dat zijn de nulpunten en het snijpunt met de y-as;
-
de asymptoten;
-
de toppen, de punten met (locale) maxima en minima, die je met de grafische rekenmachine kunt opzoeken.
Heb je die allemaal in beeld, dan kan een grafische rekenmachine die karakteristieken voor je vinden.
Hij heeft een menu waarmee ze allemaal kunnen worden berekend.
‡

Voorbeeld 1
Je ziet op veel plaatsen windmolens om elektriciteit op te wekken.
Het vermogen dat zo'n molen levert hangt af van de dubbele wieklengte D in m en van de windsnelheid v in m/s.
Het vermogen van een zeker type windmolen met D = 10 m wordt gegeven door de formule:
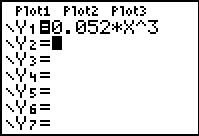
P = 0,052 · v3.
Met je grafische rekenmachine kun je hierbij een grafiek maken. Maak een goede grafiek.
Antwoord
Je voert de formule in als Y1=0.052*X^3.
Maar wat zijn verstandige vensterinstellingen?
Kijk allereerst naar de invoerwaarden, dus die voor de windsnelheid v.
Negatieve windsnelheden bestaan niet, dus je begint bij v = 0. Vervolgens google je even en vind je dat stormkracht begint bij ongeveer 20,8 m/s. Dan zullen ze windmolens vast niet langer laten draaien. Dus lijkt maximaal v = 20 m/s wel genoeg. Bekijk vervolgens de tabel: P blijkt van 0 tot 416 te lopen. Nu kun je het venster goed instellen.
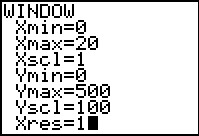
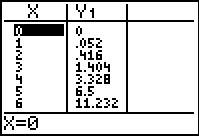
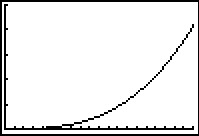
‡
Voorbeeld 2
De huurprijs van een kopieerapparaat bedraagt € 250,00 per maand.
Het maken van een kopie kost € 0,06. Op school staat zo’n apparaat speciaal
voor gebruik door leerlingen. De leerlingen betalen € 0,10 per kopie.
Geef een formule voor de prijs per kopie (P) als functie van het aantal kopieën (a) en maak er een grafiek bij. Bij welke waarde van a maakt de school winst?
Antwoord
Als er a kopieën worden gemaakt, dan kost dit 250 + 0,06a euro.
De prijs per kopie krijg je door te delen door het aantal kopieën a.
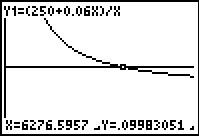
Dus: `P=250+0,06/a`.
Het aantal kopieën zal maandelijks in de duizendtallen lopen, b.v. tot: 10.000 stuks.
De prijs per kopie zal bij weinig kopieën boven de 10 cent en altijd boven de 6 cent liggen.
Neem bijvoorbeeld a van 0 t/m 10.000 en P van 0 t/m 0,20 (in euro dus).
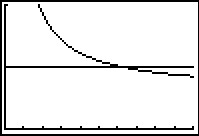
Je krijgt zo een nette grafiek, vooral als je P = 0,10 er meteen bij in zet.
Even over de grafiek lopen en je ziet dat de school bij ongeveer 6276 kopieën minder dan 10 cent per kopie kwijt is en dus winst begint te maken. De tabel geeft echter een nauwkeuriger antwoord...
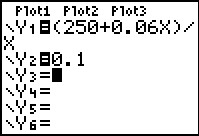
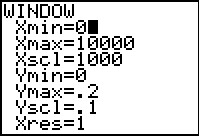
‡
Voorbeeld 3
Als de luchtweerstand geen rol speelt, dan is de baan van een afgeschoten voorwerp P een zuivere parabool.
Stel je voor dat die baan wordt beschreven door
h = –0,005x2 + x.
Hierin is x de horizontale afstand die het voorwerp heeft afgelegd (in meter) en h de bijbehorende hoogte boven de grond (in meter).
Bereken hoe hoog het voorwerp dan maximaal komt.
Antwoord
Hoe die baan er uitziet kun je je waarschijnlijk wel voorstellen: deze parabool is een mooie boog die op de grond begint en op de grond eindigt. En het voorwerp komt vast wel tientallen meters ver, dus bekijk je een tabel met x in stappen van 10 m.
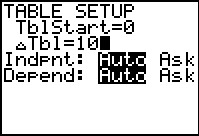
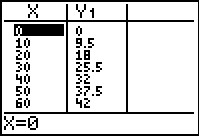
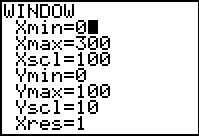
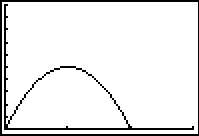
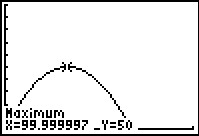
Het voorwerp lijkt ook na 60 m nog omhoog te gaan. En dus neem je bijvoorbeeld X van 0 tot 300 en Y van 0 tot 100. Inderdaad krijg je dan een mooie parabool in beeld. Het maximum kan je rekenmachine voor je berekenen, het was ook in de tabel af te lezen.
‡
Opgaven
-
Bekijk Voorbeeld 1.
-
Maak zelf de grafiek van `P=0,052v^3` met je grafische rekenmachine.
-
Bekijk ook eens hoe die grafiek er uit ziet in de standaardinstellingen van het venster.
Waarom zijn die standaardinstellingen niet geschikt in dit geval?
-
Doe nu het practicum "Functies en de GR". Bekijk alleen de stukje "Functiewaarden, nulpunten en toppen", de rest heb je pas later nodig. Ga naar
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Grafieken maken > Practicum GR
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Grafieken maken > Practicum GR
-
Neem nu bijvoorbeeld de formule `y=-0,1*x^2+2x`.
-
Maak hierbij een grafiek op je grafische rekenmachine.
Gebruik de standaardinstellingen van het venster.
-
Is de grafiek een rechte lijn?
-
Verander de instellingen van het venster. Neem `-5 <= x <= 25`.
Waarom zijn deze instellingen beter?
-
Bepaal de nulpunten van de grafiek.
-
Bepaal de top van de grafiek.
-
Voor een abonnement voor mobiele telefonie betaal je € 24,= per maand en nog eens 8 eurocent per belminuut. De totale kosten per maand hangen dus af van het aantal belminuten per maand.
Die totale kosten kun je omrekenen naar kosten per belminuut.
-
Leg uit, dat er voor de kosten `K` per belminuut geldt: `K=0,08+(24)/a`
waarin `a` het aantal belminuten in een maand voorstelt.
-
Teken op je GR een grafiek bij deze formule. Neem aan dat `0 < a <= 240`. Bekijk eventueel Voorbeeld 2.
-
Welke asymptoten heeft de grafiek van `K`? Licht je antwoord toe.
-
Bij hoeveel belminuten betaal je 12 eurocent per minuut?
-
In Voorbeeld 3 gaat het over een parabolische baan met `h(x) = -0,005x^2 + x`.
-
Als je de grafiek met de GR wilt maken zijn de standaardinstellingen van het venster niet geschikt. Waarom niet?
-
Om het hoogste punt te kunnen bepalen moet je de grafiek goed in beeld hebben.
Hoe bepaal je welke waarden van `x` je moet instellen?
-
Maak vervolgens met je GR een geschikte tabel om te bekijken welke functiewaarden er allemaal voorkomen.
-
Bij welke vensterinstellingen komt de hele baan in beeld?
-
Bepaal nu de maximale hoogte van het voorwerp boven de grond.
Verwerken
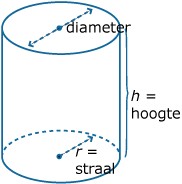 Voor de inhoud van een cilindervormig blikje geldt: `V = pi * r^2 * h`.
Voor de inhoud van een cilindervormig blikje geldt: `V = pi * r^2 * h`.
Hierin is `V` de inhoud (het volume), `r` de straal in centimeter en `h` de hoogte in centimeter.
Neem een blikje waarvoor `h = 10` cm. Nu is `V` een functie van `r`.
-
Schrijf de formule van deze functie op.
-
Breng de grafiek van deze functie zo in beeld dat je bij `V = 1000` nog kunt aflezen hoe groot `r` is.
Bepaal de waarde van `r` in één decimaal nauwkeurig.
Voor een blikje waarvan de diameter en de hoogte gelijk zijn, geldt: `h = 2r`.
-
Schrijf een bijpassende formule op voor `V` als functie van `r`.
-
Bepaal nu in één decimaal nauwkeurig de waarde van `r` van zo'n blik als de inhoud 0,5 L is.
-
Voor een kopieerapparaat bedraagt de maandelijkse huur € 200,- waarbij nog
een bedrag van 4 cent per kopie komt.
`K` stelt de totale kosten (in €) voor en `a` is het aantal kopieën dat er maandelijks (gemiddeld) wordt gemaakt.
-
Schrijf een formule op voor `K` als functie van `a`.
-
Iemand die een kopie maakt betaalt 10 cent per kopie.
Schrijf een formule op voor de maandelijkse inkomsten `I` als functie van `a`.
-
Hoeveel kopieën moeten er per maand worden gemaakt als 10 cent per kopie kostendekkend is?
-
Breng van de volgende formules de grafieken in beeld. Denk om het gebruik van haakjes en de instellingen van het venster!
-
`R = 250p - 0,5p^2`
-
`k = 0,04 + 200/a`
-
`N = 60 / (30 + 0,5d)`
-
Voor de totale kosten (`TK`) bij de productie van een bepaald artikel geldt:
`TK = 100 + 0,1q^2`
waarin `q` het aantal exemplaren voorstelt.
-
Bereken de gemiddelde kosten per exemplaar bij een productie van 120 stuks in twee decimalen nauwkeurig.
-
Stel een formule op voor de gemiddelde kosten per exemplaar (`GTK`) als functie van `q`.
-
Welke verticale asymptoot heeft de functie `GTK`?
-
Waarom is er nu geen horizontale asymptoot?
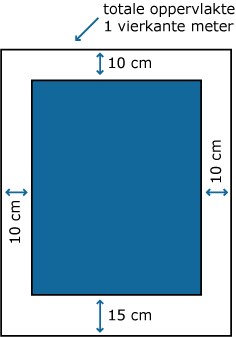 Stel je voor dat een bedrijf affiches wil maken. Om op te vallen moet de oppervlakte van zo’n affiche 1 m2 worden.
Het affiche wordt zo bedrukt, dat er aan de beide zijkanten en de bovenkant een witte strook van 10 cm overblijft.
Aan de onderkant is die strook 15 cm.
De bedrijfsleiding vraagt zich af welke afmetingen het affiche nu nog kan hebben.
Ze komen daarbij op de formule `(l + 25)*(b + 20) = 10000`.
Stel je voor dat een bedrijf affiches wil maken. Om op te vallen moet de oppervlakte van zo’n affiche 1 m2 worden.
Het affiche wordt zo bedrukt, dat er aan de beide zijkanten en de bovenkant een witte strook van 10 cm overblijft.
Aan de onderkant is die strook 15 cm.
De bedrijfsleiding vraagt zich af welke afmetingen het affiche nu nog kan hebben.
Ze komen daarbij op de formule `(l + 25)*(b + 20) = 10000`.
-
Laat zien hoe ze aan deze formule komen en wat de variabelen `l` en `b` betekenen.
-
Herschrijf de formule tot `l` een functie is van `b`.
Breng de grafiek van deze formule in beeld.
-
Controleer of alle in beeld gebrachte afmetingen ook mogelijk zijn.
-
Bij nader inzien wil de bedrijfsleiding dat het bedrukte deel een vierkant wordt. Welke maat voor de affiches adviseer je nu?
Testen
-
In een biologisch laboratorium is onderzoek gedaan naar de tijd die zaden nodig hebben om voor 50% te ontkiemen. Proefondervindelijk is een verband tussen temperatuur en kiemtijd gebleken. De kiemtijd `K` is geteld in dagen en de temperatuur `T` is gemeten in °C.
Dit verband wordt gegeven door: `K=89/(T-2)`.
-
Boven welke temperatuur is de helft van de zaden al binnen 10 dagen ontkiemd?
-
Welke waarden voor `T` zijn nu zinvol?
-
Welke asymptoten heeft de grafiek van deze functie?
-
Welke waarden kan `K` aannemen?
-
Bij een bepaald artikel is het verband tussen de verkochte hoeveelheid `q` en de prijs `p` (in €): `q = 10000 - 20p`.
Voor de opbrengst `R` (in €) geldt: `R = p * q`.
Voor de kosten `K` (in €) geldt: `K = 15000 + 100q`.
Voor de winst geldt: `W = R - K`.
-
Stel een formule op voor `R` als functie van `q`.
-
Welke waarden kunnen `p` en `q` aannemen?
-
Schrijf `W` als functie van `q`.
-
Maak een grafiek van de formule voor de winst.
Let op de waarden die `q` kan aannemen en zorg voor een zodanige grafiek dat alle mogelijke waarden van `W` in beeld komen.
De winst loopt in de tonnen!
-
Bepaal voor welke verkochte hoeveelheid de winst maximaal is.
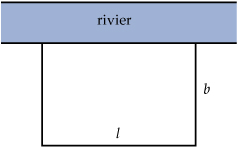 Boer Voortman zet voor zijn paard een weilandje af. Hij heeft daarvoor nog 200 m gaas. Het weiland wordt zuiver rechthoekig.
Omdat het weiland tegen een brede rivier aan komt te liggen hoeft hij alleen de twee breedtes en de lengte van gaas te voorzien.
Boer Voortman zet voor zijn paard een weilandje af. Hij heeft daarvoor nog 200 m gaas. Het weiland wordt zuiver rechthoekig.
Omdat het weiland tegen een brede rivier aan komt te liggen hoeft hij alleen de twee breedtes en de lengte van gaas te voorzien.
-
Druk de lengte `l` van het weiland uit in de breedte `b`.
-
Druk de oppervlakte `A` van het weiland uit in `b`.
-
Breng met je grafische rekenmachine de grafiek bij de formule voor `A` in beeld.
-
Voor welke waarde van `b` is de oppervlakte van het weiland zo groot mogelijk?
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Grafieken maken > Practicum GR
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Formules en grafieken > Grafieken maken > Practicum GR





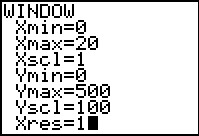











 Voor de inhoud van een cilindervormig blikje geldt: `V = pi * r^2 * h`.
Voor de inhoud van een cilindervormig blikje geldt: `V = pi * r^2 * h`. Stel je voor dat een bedrijf affiches wil maken. Om op te vallen moet de oppervlakte van zo’n affiche 1 m2 worden.
Het affiche wordt zo bedrukt, dat er aan de beide zijkanten en de bovenkant een witte strook van 10 cm overblijft.
Aan de onderkant is die strook 15 cm.
De bedrijfsleiding vraagt zich af welke afmetingen het affiche nu nog kan hebben.
Ze komen daarbij op de formule `(l + 25)*(b + 20) = 10000`.
Stel je voor dat een bedrijf affiches wil maken. Om op te vallen moet de oppervlakte van zo’n affiche 1 m2 worden.
Het affiche wordt zo bedrukt, dat er aan de beide zijkanten en de bovenkant een witte strook van 10 cm overblijft.
Aan de onderkant is die strook 15 cm.
De bedrijfsleiding vraagt zich af welke afmetingen het affiche nu nog kan hebben.
Ze komen daarbij op de formule `(l + 25)*(b + 20) = 10000`.
 Boer Voortman zet voor zijn paard een weilandje af. Hij heeft daarvoor nog 200 m gaas. Het weiland wordt zuiver rechthoekig.
Omdat het weiland tegen een brede rivier aan komt te liggen hoeft hij alleen de twee breedtes en de lengte van gaas te voorzien.
Boer Voortman zet voor zijn paard een weilandje af. Hij heeft daarvoor nog 200 m gaas. Het weiland wordt zuiver rechthoekig.
Omdat het weiland tegen een brede rivier aan komt te liggen hoeft hij alleen de twee breedtes en de lengte van gaas te voorzien.