Formules gebruiken

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Werken met formules > Formules gebruiken > Inleiding

Als je nog nooit met een grafische rekenmachine hebt gewerkt, doe je nu eerst het practicum "Basistechnieken". Je vindt het bij: Practicum GR.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Werken met formules > Formules gebruiken > Uitleg

Opgaven

  1. Gebruik de formule: oppervlakte(rechthoek) = lengte × breedte.
    1. Stel dat gegeven is: lengte = 6 m. Vul dit in de formule in. Geef de formule die hierdoor ontstaat.
    2. Stel je voor dat: oppervlakte = 12 m2. Schrijf op hoe de formule dan wordt.
    3. Van een rechthoek is bekend dat het een vierkant is. Schrijf de formule op die voor deze rechthoek het verband tussen oppervlakte en lengte beschrijft.
    4. De volgende grafieken horen bij de formules uit a, uit b of c. Schrijf bij elke grafiek de juiste formule, zet de juiste variabelen bij de assen en maak er een goede schaalverdeling bij.

            

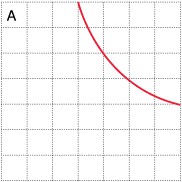
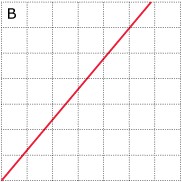
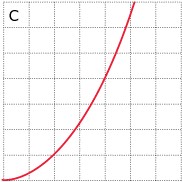
  2. Als de omtrek van een rechthoek 60 cm is, dan geldt voor de lengte `l` en de breedte `b`: `2l+2b=60`.
    Bekijk de formule `2l+2b=60` in de Uitleg.
    1. Waarom kun je deze formule zo niet in de grafische rekenmachine invoeren?
    2. De formule is te herschrijven tot `b=30-l`. Voer nu de formule in de grafische rekenmachine in. Neem voor het venster de standaardinstellingen en schrijf op welke formule je precies invoert.
    3. Waarom krijg je nu geen grafiek in beeld?
    4. Stel je venster zo in dat `0 <= x <= 30` en `0 <= y <= 30`. Waarom krijg je nu de hele grafiek in beeld?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Werken met formules > Formules gebruiken > Theorie

Bekijk eerst de Theorie. De Voorbeelden moet je in de opgaven opzoeken en doornemen.

Opgaven

  1. Bekijk de Voorbeelden 1 en 2.
    Je wilt een grafiek maken bij de formule `2l+2b=100`.
    1. Hoe doe je dat "met de hand"?
    2. Hoe doe je dat met de grafische rekenmachine? Waarom moet je de formule eerst herschrijven?
    3. Schrijf de formule zo, dat `l` een functie is van `b`.
    4. Bij welke waarde van `b` geldt `l=7,5`?

  2. Bekijk Voorbeeld 3. Schrijf de volgende formules zo, dat `y` is uitgedrukt in `x` en maak de grafiek op de grafische rekenmachine
    1. `3x+y=6`
    2. `x*y=12`
    3. `x=4-y`
    4. `2x-3y=6`
    5. `x^2+4y=8`
    6. `0,5x+1,5y=12`

  3. Bij welke van de volgende formules kun je een grafiek maken? Schrijf in dat geval de formule zo, dat je hem in de grafische rekenmachine kunt invoeren.
    1. inhoud = `3r^2` met `r` in cm
    2. inhoud = `l * b * h` met `l`, `b` en `h` in cm
    3. `4(a - b) = 4a - 4b`
    4. `l * b = 20` met `l` en `b` in m

  4. De Quetelet-index (`QI`) is een maat voor je gezondheid.
    Je berekent de `QI` met de formule: `QI=G/(l^2)`.
    Hierin is `l` je lengte in meters en `G` je gewicht in kilogram.
    Een `QI` van tussen de 20 en de 25 betekent een gezond gewicht.
    1. Bereken de `QI` van iemand die 180 centimeter lang is en 78 kilogram weegt.
    2. Bij een `QI` van 20 kun je een grafiek maken van iemands gewicht afhankelijk van zijn lengte. Teken die grafiek.
    3. Teken in hetzelfde assenstelsel de grafiek `QI = 25`.
    4. Stel je een persoon voor van 180 centimeter lengte. Geef in je figuur aan welke gewichten voor deze persoon gezond zijn. Zet de ondergrens en de bovengrens er in de grafiek bij, in kilogram nauwkeurig.

  5. Bekijk Voorbeeld 4. Werk in de volgende uitdrukkingen de haakjes uit:
    1. `3x * (x - 2y)`
    2. `2a - (9a + 6)`
    3. `0,5p^2 * (100 - p) - p * (20p + 100)`
    4. `-5p^3(p^2 - 3p^3)`

  6. Bekijk Voorbeeld 4. Werk in de volgende uitdrukkingen de haakjes uit:
    1. `(x + 2) * (x + 4)`
    2. `2(b + 4)(b - 2)`
    3. `(l + 3)(1/l + 6)`
    4. `(5c - 4)^2`

Verwerken

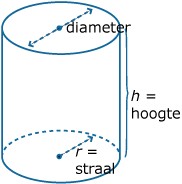  1. Voor de inhoud van een cilindervormig blikje geldt: `V = pi * r^2 * h`.
    Hierin is `V` de inhoud (het volume), `r` de straal in centimeter en `h` de hoogte in centimeter.
    1. In welke eenheid moet `V` worden uitgedrukt?
    2. Hoeveel bedraagt de inhoud van een blikje met een diameter van 80 millimeter en een hoogte van 16 centimeter?
    3. Welke formule geeft het verband tussen `V` en `r` voor blikjes met een hoogte van 16 centimeter?
    4. Teken een grafiek bij de formule die je in c hebt gevonden.
    5. Van andere blikjes ligt de inhoud vast: `V = 1` L. Welk verband is er nu tussen `r` en `h`? Teken er een grafiek van.

  2. Welke van deze formules beschrijft een verband tussen twee variabelen? Teken er dan een grafiek bij.
    1. inhoud(kubus) = `r^3`
    2. `s = 400 - 5t^2`
    3. `a^2 + b^2 = c^2`

  3. Schrijf de volgende formules zo, dat `y` een functie is van `x`.
    1. `2x+4y=10`
    2. `2x-3y+6=0`
    3. `0,5y^2=8x`
    4. `x^2*y=6`

  4. Werk de haakjes uit:
    1. `-2x(x^2+6x)`
    2. `-2x-(x^2+6x)`
    3. `(t+20)(t-5)`
    4. `(x^2+1)(3x-2)`
    5. `(a-3)(a+3)`
    6. `(6x - 3)^2`

  5. Een ondernemer verkoopt een bepaald artikel. Er bestaat een verband tussen de hoeveelheid `q` die per maand van dit artikel wordt verkocht en de prijs `p` (in € per verkochte eenheid). Dit verband wordt beschreven door de formule: `q = 4000 - 20p`.
    1. Hoeveel eenheden van dit artikel verkoopt hij in een bepaalde maand als € 50,- per eenheid rekent?
    2. De ondernemer koopt dit artikel in voor € 30,- per eenheid. Wil hij geen verlies lijden dan is dit zijn laagste verkoopprijs. Hoeveel eenheden kan hij dan maximaal maandelijks verkopen?
    3. Negatieve waarden voor `q` zijn onmogelijk. Tot hoever zou de verkoopprijs dus kunnen oplopen?
    4. De opbrengst per maand bereken je door de prijs `p` per stuk te vermenigvuldigen met de verkochte hoeveelheid per maand. Laat zien dat `R=4000p-20p^2`.
    5. Maak een tabel voor de opbrengst waarbij `p=30,40,50,60,...,2000`. Gebruik je grafische rekenmachine.
    6. Bij welke prijs heeft deze ondernemer de grootste maandelijkse opbrengst?

Testen

  1. Bij welke van de volgende formules kun je een grafiek maken? Schrijf de op hoe je die formule in de grafische rekenmachine moet invoeren.
    1. `a + b = 8`
    2. `4x^2 - 25 = 135`
    3. `R = 50p - 2p^2`

  2. Werk de haakjes uit:
    1. `p(2p+1)`
    2. `(4+k)(5-2k)`
    3. `(b+5)^2`

  3. Een boer heeft een zuiver vierkant stuk land. Hij staat een strook van 3 m breed aan de zuidkant van zijn land af voor de aanleg van een fietspad. Ter compensatie krijgt hij aan de oostkant een strook van 3 m terug.
    1. Noem de oorspronkelijke lengte van het land `x` (meter). Hoe groot is dan de oppervlakte van het land voor de aanleg van het fietspad?
    2. Hoe groot is de oppervlakte van het land na aanleg van het fietspad? (Maak eerst een schets van de situatie. Let op de haakjes!)
    3. Laat door uitwerken van de haakjes zien dat de boer spijt zal hebben van de compensatieregeling.