
Grafieken combineren en vergelijken
Inleiding
Regelmatig heb je te maken met meerdere grafieken in één figuur. Soms zet je bijvoorbeeld op de verticale as zowel de kosten als de opbrengst uit tegen het aantal verkochte exemplaren. Dan kan het interessant zijn om naar het snijpunt van beide grafieken te kijken, daar begin je winst te maken...
Ook kun je een afzonderlijke winstgrafiek maken door opbrengst en kosten van elkaar af te trekken.
Je leert nu:
- grafieken vergelijken en snijpunten aflezen en interpreteren;
- werken met somgrafiek en verschilgrafiek;
- grafieken schakelen.
Je kunt al:
- grafieken tekenen en de eigenschappen van grafieken herkennen;
- waarden uit grafieken aflezen.
Verkennen
Je ziet hier in één figuur de opbrengst en de kosten van een fabrikant bij de verkoop van een bepaald artikel.
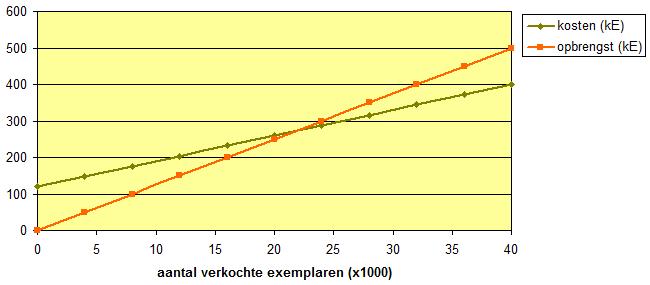
> Het snijpunt van beide grafieken wordt wel 'break-even-point' genoemd. Begrijp je waarom?
> Teken de grafiek van de winst uitgezet tegen de verkochte hoeveelheid.
Uitleg
De grafieken bij Verkennen laten de opbrengst en de kosten in k€ (duizenden Euro) zien bij de verkoop van een bepaald artikel.
Beide grafieken ontstaan vanuit tabellen, zowel de opbrengst als de kosten hangen af van het aantal verkochte exemplaren (x 1000). Ze staan daarom in één figuur.
Het snijpunt van beide grafiek heeft een duidelijke betekenis: dan zijn opbrengst en kosten gelijk. De bijbehorende waarde van het aantal verkochte exemplaren kun je aflezen: ongeveer 22.000. Bij een verkoop van 22.000 of meer is er sprake van winst.
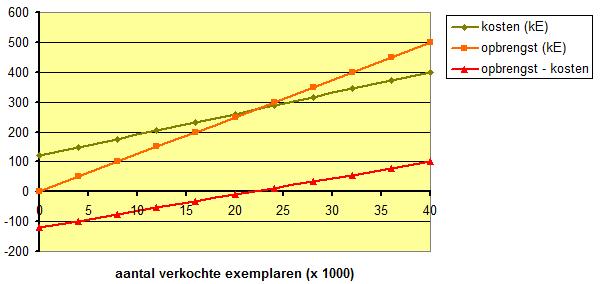
Je kunt hiermee ook de grafiek maken van de winst: je trekt dan opbrengst en kosten van elkaar af.
De verschilgrafiek van opbrengst en kosten is de winstgrafiek. Je ziet ook nu dat de winst pas positief is bij een verkoop van 22.000 artikelen of meer.
‡
Opgaven
-
In de Uitleg zie je de grafieken van de opbrengst, de kosten en de winst bij de verkoop van een bepaald artikel.
Hier zie je tabellen van de opbrengst en de kosten.

-
Laat zien hoe tabel voor de winstgrafiek uit de voorgaande twee tabellen kan ontstaan.
-
Kun je het snijpunt van beide grafieken met deze tabellen nauwkeuriger benaderen?
Zo ja, laat zien hoe dan.
Theorie
Soms heb je te maken met meerdere grafieken.
Kun je twee variabelen uitdrukken in dezelfde eenheden en hangen beide van dezelfde variabele af, dan kun je de bijbehorende grafieken in één figuur tekenen. Zie Voorbeeld 1.
-
In een snijpunt van beide grafieken hebben de twee variabelen op de verticale as dezelfde waarde.
-
Je maakt een somgrafiek door steeds bij elkaar passende uitkomsten op te tellen.
-
Je maakt een verschilgrafiek door steeds bij elkaar passende uitkomsten van elkaar af te trekken.
Heb je te maken met twee grafieken waarbij in de éne grafiek een variabele y afhangt van x en in de andere x weer afhangt van t, dan kun je deze variabelen schakelen: bij een waarde van t vind je een waarde van x en dan daarbij weer een passende waarde van y.
Zie Voorbeeld 2.
‡
Voorbeeld 1
In deze grafieken van twee hardlopers kun je zien hoe beiden de Coopertest (12 minuten hardlopen) afleggen. Elk rondje van 400 m wordt hun tijd geklokt, het gaat om het afleggen van een zo groot mogelijke afstand.
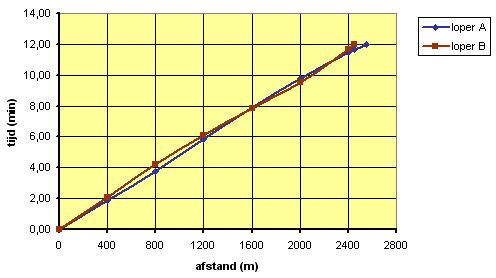
- Hoeveel minuten ligt loper B voor op loper A?
- Wie van beiden levert de beste prestatie?
- Maak een bijpassende verschilgrafiek.
Antwoord
De snijpunten van beide grafieken kun je aflezen (schatten): (1500; 7,50) en (2250; 11,00).
Loper B ligt voor als hij minder tijd nodig heeft voor dezelfde afstand als loper A, dus van 7,5 minuten tot 11 minuten, dat is ongeveer 3,5 minuten.
Loper A levert de beste prestatie: hij loopt 2554 m in 12 minuten (zie tabel).
De verschilgrafiek maak je door eerst een verschiltabel en daarvan een grafiek te maken.
‡
Voorbeeld 2
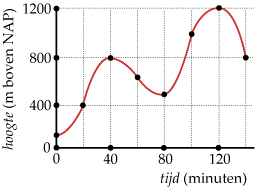
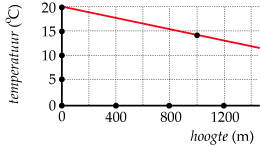
Beide grafieken geven informatie over een bergwandeling.
De variabele tijd geeft het aantal minuten na het begin van de wandeling.
- Hoeveel bedraagt de temperatuur na 80 minuten lopen?
- Hoeveel bedraagt het temperatuursverschil tussen begin en eind van de wandeling?
Antwoord
Na 80 minuten lopen zit de wandelaar op 500 m hoogte.
In de tweede grafiek zie je dat de temperatuur op die hoogte ongeveer 17°C is.
Op deze manier schakel je de drie variabelen tijd –> hoogte –> temperatuur.
Aan het begin van de wandeling zit je op ongeveer 150 m hoogte, de temperatuur is dan ongeveer 19°C. Aan het einde van de wandeling zit je op 800 m hoogte, de temperatuur is dan ongeveer 15°C.
Het temperatuursverschil is daarom ongeveer 4°C.
‡
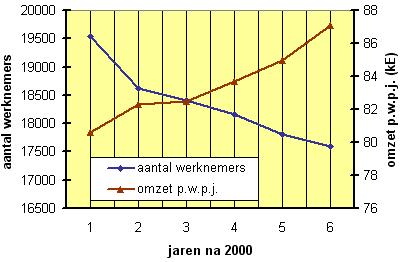
Voorbeeld 3
In deze grafiek zie je hoe binnen een groot bedrijf het aantal werknemers terugloopt, terwijl (o.a. door automatisering) de omzet per werknemer per jaar stijgt.
Beide grafieken snijden elkaar. Leg uit waarom dit snijpunt geen enkele betekenis heeft en bereken de totale omzet van het bedrijf in dat jaar.
Antwoord
Er zijn twee verschillende verticale assen: op de linker as lees je het aantal werknemers af, op de rechter as de omzet per werknemer per jaar (in duizenden euro).
In het punt waar beide grafieken elkaar lijken te snijden (in 2003 dus) is het aantal werknemers ongeveer 18350 en de omzet p.w.p.j. ongeveer € 82.500. Deze uitkomsten zijn totaal verschillend.
Wel kun je zo gemakkelijk de totale jaaromzet van het bedrijf uitrekenen...
‡
Opgaven
-
Bekijk de grafieken van twee hardlopers in Voorbeeld 1.
-
Controleer nog even de afgelezen snijpunten van beide grafieken.
-
Maak nu zelf een verschiltabel en een verschilgrafiek.
-
Op welke plaatsen gaat je verschilgrafiek door de horizontale as?
En wat betekent dit?
-
Gebruik de grafieken bij de bergwandeling uit Voorbeeld 2.
-
Hoeveel bedraagt de temperatuur na 40 minuten lopen?
-
Hoeveel bedraagt de temperatuur na 100 minuten lopen?
-
Op welke twee momenten is de temperatuur hetzelfde als na 60 minuten lopen?
-
Hoeveel bedraagt het temperatuursverschil tussen het warmste en het koudste moment van de wandeling?
-
In Voorbeeld 3 vind je twee grafieken die het aantal werknemers en de omzet van een bedrijf beschrijven.
-
Waarom heeft het snijpunt van beide grafieken geen betekenis?
-
Hoeveel bedraagt de totale jaaromzet in 2003?
-
Hoeveel bedraagt de totale jaaromzet in 2006?
-
Betekent de daling van het aantal werknemers ook een daling van de omzet? En hoe zit het waarschijnlijk met de winst?
Verwerken
-
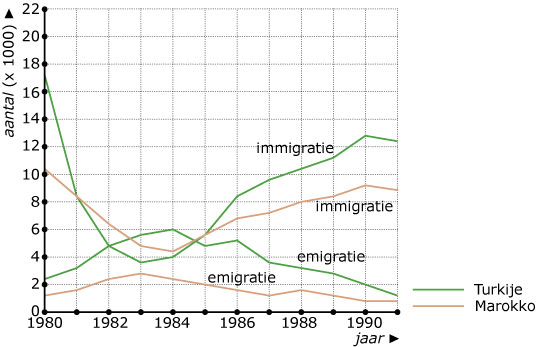
Onder het migratiesaldo wordt het verschil verstaan tussen het aantal
mensen dat naar Nederland immigreert en het aantal mensen dat uit
Nederland emigreert. In de grafiek vind je gegevens over de migratie
van Marokkanen en Turken van en naar Nederland in de periode 1980 - 1991.
-
Welke betekenis hebben de snijpunten van de grafieken van "immigratie" en "emigratie" bij dezelfde bevolkingsgroep?
-
Welke betekenis hebben de snijpunten van de twee immigratiegrafieken?
-
Welke van deze beide bevolkingsgroepen kende in een deel van deze periode een negatief migratiesaldo?
-
Kun je op grond daarvan zeggen dat deze bevolkingsgroep in Nederland in aantal achteruit ging?
-
Opvallend is het feit dat in de jaren 1982 - 1984 de immigratie veel lager is dan in de andere jaren en de emigratie juist wat hoger is. Geef daar redenen voor.
-
Teken de grafiek van het migratiesaldo van de Turken.
-
In welk jaar daalt dit migratiesaldo het sterkst?
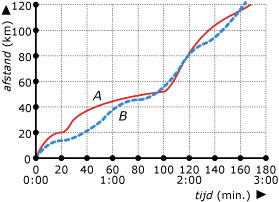 Je ziet hier de grafieken van twee wielrenners die deelnemen aan een tijdrit. De grafieken zijn zo getekend dat het lijkt alsof beiden tegelijk zijn gestart (bij een tijdrit is dat niet zo).
Je ziet hier de grafieken van twee wielrenners die deelnemen aan een tijdrit. De grafieken zijn zo getekend dat het lijkt alsof beiden tegelijk zijn gestart (bij een tijdrit is dat niet zo).
-
Welke betekenis hebben de snijpunten van beide grafieken?
-
Gedurende welke periode ligt renner A voor op renner B?
-
Op welke momenten fietsen beide renners even snel?
-
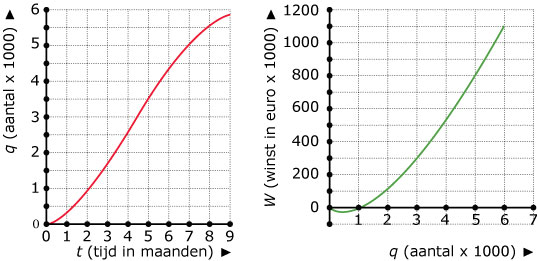
Deze grafieken laten zien hoeveel exemplaren `q` (in duizendtallen) een bepaald bedrijf van een zeker artikel heeft verkocht en hoeveel winst `W` (in duizenden euro) het daarbij heeft gemaakt. `q` is uitgezet tegen de tijd `t` in maanden na de introductie van dit artikel.
-
Hoeveel exemplaren zijn er na 4 maanden verkocht? En hoeveel winst is daarop gemaakt?
-
Tot welk aantal verkochte exemplaren werd er nog geen winst gemaakt?
-
Na hoeveel maanden werd er voor het eerst winst gemaakt?
-
Maak een tabel van de winst `W` (in duizenden euro) afhankelijk van de tijd `t` in maanden.
-
Bekijk nog eens de schoolartsenkaart voor meisjes.
Door de twee P50-grafieken te schakelen, kun je de grafiek maken van het gewicht afhankelijk van de leeftijd van een
gemiddeld meisje. Leg uit hoe je dan te werk moet gaan en teken die grafiek.
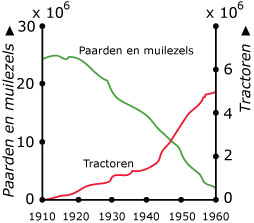 Deze figuur laat zien hoe in de vorige eeuw in de U.S.A. de paarden en muilzels als trekdieren werden vervangen door tractoren.
Deze figuur laat zien hoe in de vorige eeuw in de U.S.A. de paarden en muilzels als trekdieren werden vervangen door tractoren.
-
De grafieken hebben een snijpunt. Heeft dat enige betekenis? Licht je antwoord toe.
-
Op welk moment waren er evenveel tractoren als paarden en muilezels?
Testen
-
Twee atleten A en B deden mee aan een halve triathlon: 3 km zwemmen, 75 km fietsen en 24 km lopen.
Hun gemiddelde snelheden waren:
Atleet A: zwemmen 3 km/h; fietsen 30 km/h; lopen 12 km/h.
Atleet B: zwemmen 4 km/h; fietsen 25 km/h; lopen 16 km/h.
-
Teken in één figuur bijpassende grafieken.
-
Wie van beiden was het eerst bij de finish? Hoeveel minuten was hij op de ander voor?
-
Hebben de snijpunten van deze grafieken betekenis?
-
Kun je de vraag wie na 3 uur voor lag beantwoorden? Leg uit.
-
Bereken van beiden de gemiddelde snelheid over deze halve triathlon.
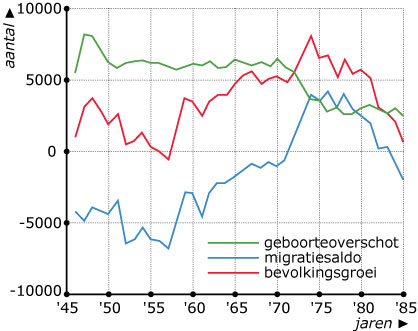 In deze figuur vind je grafieken van de bevolkingsgroei, het migratiesaldo en het
geboorteoverschot in een bepaalde regio in de periode 1946 - 1985.
In deze figuur vind je grafieken van de bevolkingsgroei, het migratiesaldo en het
geboorteoverschot in een bepaalde regio in de periode 1946 - 1985.
-
Welk verband is er tussen deze drie grafieken?
-
Er zijn twee jaren waarin het geboorteoverschot en de bevolkingsgroei gelijk zijn.
Welke jaren zijn dat? Wat betekent dat voor het migratiesaldo?
-
Wat betekent een bevolkingsgroei van 0 voor het migratiesaldo en het geboorteoverschot?
In welke jaren is dat het geval?
-
In welke periode is het geboorteoverschot vrijwel constant?
Wat betekent dat voor de grafieken van het migratiesaldo en de bevolkingsgroei?
-
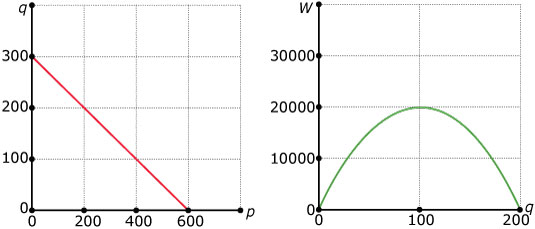
De winst `W` op een bepaald artikel hangt af van de prijs per stuk `p` en de
hoeveelheid `q` die wordt verkocht. De grafieken geven het verband tussen `W`, `p`
en `q` weer. Teken een grafiek van `W` uitgezet tegen `p`.








 Je ziet hier de grafieken van twee wielrenners die deelnemen aan een tijdrit. De grafieken zijn zo getekend dat het lijkt alsof beiden tegelijk zijn gestart (bij een tijdrit is dat niet zo).
Je ziet hier de grafieken van twee wielrenners die deelnemen aan een tijdrit. De grafieken zijn zo getekend dat het lijkt alsof beiden tegelijk zijn gestart (bij een tijdrit is dat niet zo).

 Deze figuur laat zien hoe in de vorige eeuw in de U.S.A. de paarden en muilzels als trekdieren werden vervangen door tractoren.
Deze figuur laat zien hoe in de vorige eeuw in de U.S.A. de paarden en muilzels als trekdieren werden vervangen door tractoren.
 In deze figuur vind je grafieken van de bevolkingsgroei, het migratiesaldo en het
geboorteoverschot in een bepaalde regio in de periode 1946 - 1985.
In deze figuur vind je grafieken van de bevolkingsgroei, het migratiesaldo en het
geboorteoverschot in een bepaalde regio in de periode 1946 - 1985.
