
Waarden toevoegen
Inleiding
Grafieken en tabellen worden vooral gemaakt om het verloop van een bepaalde variabele afhankelijk van bijvoorbeeld de tijd duidelijk in beeld te krijgen. En waarom wil men dat? Om voorspellingen te kunnen doen, of tussenliggende waarden te kunnen vaststellen. Het gaat dus vrijwel altijd om het toevoegen van nieuwe waarden op grond van het verloop in de tabel of de grafiek. Maar zoiets kun je niet zomaar doen...
Je gebruikt de regelmaat die je aantreft, de eigenschappen van de grafieken...
Je leert nu:
- grafieken gebruiken om waarden toe te voegen in tabellen, interpoleren en extrapoleren;
- waarden toevoegen in periodieke grafieken;
- waarden aflezen in bundels grafieken.
Je kunt al:
- grafieken tekenen en de eigenschappen van grafieken herkennen;
- de periode in een zich herhalende grafiek herkennen.
Verkennen
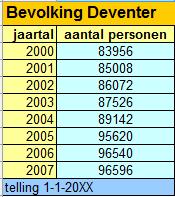
Hier zie je een tabel van de bevolking van Deventer.
Het aantal mensen hangt af van de tijd (jaartal).
Je kunt de tabel of een bijpassende grafiek gebruiken om de bevolking op tussenliggende of toekomstige tijdstippen te voorspellen.
> Hoeveel mensen telde Deventer op 1 juli 2002 ongeveer?
> Waarom kun je het aantal mensen op 1 juli 2004 heel moeilijk schatten?
> Schat het aantal mensen in Deventer op 1 januari 2020.

Uitleg
Uit de Wikipedia: "De huisstofmijt (Dermatophagoides pteronyssinus) is een haast onzichtbaar kleine (ca. 0,3 mm) mijt die in huisstof leeft, met name in matrassen, kussens, gestoffeerd meubilair, tapijt en op beschimmelde muren. De huisstofmijt komt overal ter wereld voor, in alle klimaten, behalve op grote hoogte waar hij zich moeilijk kan voortplanten. Hij gedijt het beste bij ongeveer 25 graden Celsius en een luchtvochtigheid van 50-75%."

Je ziet hier grafieken van het aantal huisstofmijten dat ontstaat uit een kleine beginpopulatie bij de juiste leefomstandigheden. Elke grafiek beschrijft het aantal mijten uitgezet tegen de tijd in dagen, steeds bij een andere temperatuur. Dit is een grafiekenbundel, de getekende punten zijn de echte meetpunten. Hiermee kun je:
- Schatten dat het aantal mijten na 55 dagen bij een temperatuur van 25°C ongeveer 256 bedraagt, terwijl dit bij een temperatuur van 21°C slechts ongeveer 92 is. Je doet dit door af te lezen van de rechte lijnstukjes tussen twee meetpunten. Je spreekt dan van interpoleren tussen twee punten.
- Schatten dat het aantal mijten na 75 dagen bij een temperatuur van 25°C ongeveer 347 bedraagt, terwijl dit bij een temperatuur van 21°C slechts ongeveer 154 is. Je doet dit door de rechte lijnstukjes van de laatste twee meetpunten door te trekken. Je spreekt dan van extrapoleren.
- Schatten dat het aantal mijten na 55 dagen bij een temperatuur van 23°C vermoedelijk ongeveer evenveel zal zijn als bij een temperatuur van 28,5°C.
‡
Opgaven
-
Bekijk de grafieken van het aantal huisstofmijten in de Uitleg.
-
Controleer de schatting van het aantal mijten bij een temperatuur van 21°C na 55 dagen.
-
Controleer de schatting van het aantal mijten bij een temperatuur van 25°C na 75 dagen.
-
Wat is het verschil tussen interpoleren en extrapoleren?
-
Schat het aantal mijten na 55 dagen bij een temperatuur van 23°C.
Leg uit dat dit aantal vermoedelijk overeen komt met dat bij een temperatuur van 28,5°C.
-
Bekijk de grafieken van het aantal huisstofmijten nog eens.
-
Hoeveel huisstofmijten waren er bij het begin van het onderzoek naar hun groei?
-
Hoeveel zijn er na 40 dagen bij een temperatuur van 21°C?
Met hoeveel procent is het aantal dus in die 40 dagen toegenomen?
-
Beantwoord dezelfde vragen als bij b maar nu bij een temperatuur van 20°C.
-
Schets de grafiek van de groei van huisstofmijten bij 20°C.
-
Waarom kun je de grafiek bij 26°C niet tekenen op grond van de gegeven grafieken alleen?
Theorie
Veel grafieken horen bij tabellen met metingen.
Hoe je de meetpunten verbindt, blijft een keuze. Bij een lijngrafiek trek je er rechte lijnstukken tussen, soms een vloeiende kromme. Waarden die niet in de tabel voorkomen, kun je alleen schatten:
- interpoleren is het schatten van punten tussen twee meetpunten, vaak doe je dit door er een lijnstukje tussen te trekken en dan af te lezen (halverwege 2002 waren er ongeveer 870.000 personen);
- extrapoleren is het schatten van punten buiten het gebied met meetpunten, vaak doe je dit door een lijnstukje tussen de twee voorgaande (of de twee opvolgende) meetpunten te verlengen en dan af te lezen (begin 2008 ongeveer 968.000 personen).
Soms heb je te maken met meerdere grafieken die bij dezelfde variabelen op de assen horen.
Dat is een grafiekenbundel. Ook daarin kun je waarden aflezen die niet in de tabellen voorkomen, zelfs in het gebied tussen twee grafieken.
‡
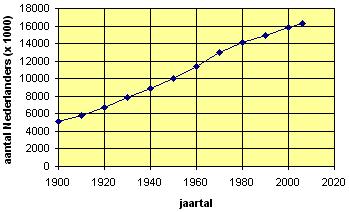
Voorbeeld 1
Je ziet hier een grafiek van het aantal Nederlanders (× 1000) uitgezet tegen het jaartal.
Schat door interpoleren het aantal Nederlanders in 1925.
Schat door extrapoleren het aantal Nederlanders in 2020.
Antwoord
Er zijn al rechte lijnstukjes getrokken tussen de meetpunten.
Je zoekt 1925 op de horizontale as en leest af: ongeveer 7500, dus 7,5 mln Nederlanders.
Om het aantal Nederlanders in 2020 te kunnen bepalen verleng je het lijnstukje behorende bij de laatste twee meetpunten.
Ga na, dat je dan ongeveer 17500 afleest bij 2020, dus ongeveer 17,5 mln Nederlanders.
‡
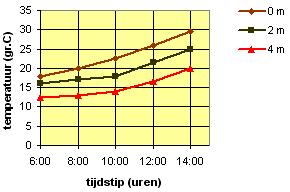
Voorbeeld 2
Je ziet hier een bundel grafieken van de watertemperatuur (in °C) afhankelijk van het tijdstip op de dag. Er is gemeten in een groot meer op een tropische dag. De watertemperatuur loopt in de loop van de ochtend al behoorlijk op. Maar het is niet op elke diepte even warm.
Hoe warm is het om 13:00 uur op 1 m diepte?
Waarom heeft extrapoleren naar 15:00 uur niet veel zin?
Antwoord
Om 13:00 uur is het op 0 m diepte ongeveer 27,5 graden.
Om 13:00 uur is het op 2 m diepte ongeveer 23 graden.
Op 1 m diepte zal het op dat tijdstip daar ongeveer 25,5°C zijn.
Het heeft weinig zin om de watertemperatuur voorbij de 14:00 uur te extrapoleren, want daarna gaat de zon weer zakken en zal de opwarming niet meer zo sterk zijn, hoewel hij nog wel even door gaat...
‡
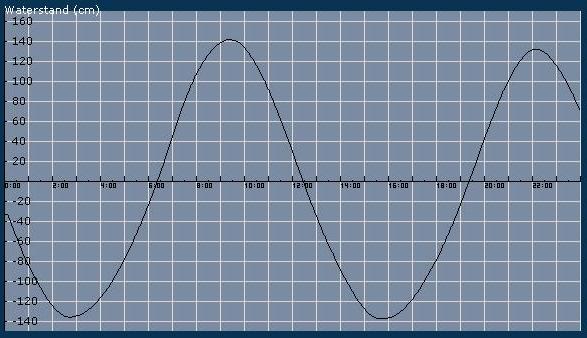
Voorbeeld 3
Op www.getij.nl vind je bij "Getijvoorspellingen" de waterstanden voor de komende dagen op verschillende locaties in Nederland en op de Noordzee.
Deze grafiek van de waterstanden in Harlingen was er op zeker moment te vinden.
Als je nu de waterstand om 14:00 uur de volgende dag wilt weten, hoe ga je dan te werk?
Antwoord
Omdat de waterstand periodiek is, heeft extrapoleren door het eind van de grafiek door te trekken geen enkele zin.
Nu maak je gebruik van de periode van de grafiek.
De waterstand kent een periode van ongeveer 12 uur en 20 minuten.
Je kunt dat in de grafiek ook zien...
Dit betekent dat de grafiek om de 12 uur en 20 minuten (ongeveer) dezelfde waterstand aangeeft.
De waterhoogte om 14:00 uur de volgende dag is daarom hetzelfde als die om 01:40 uur de volgende dag.
En ook hetzelfde als die op 13:20 uur van deze dag. En die waterstand kun je uit de grafiek aflezen.
(De waterstand is wel erg afhankelijk van het weer, van wind en regen, dus heel erg betrouwbaar is deze schatting niet.)
‡
Opgaven
-
Bekijk de grafiek van de bevolking van Nederland in Voorbeeld 1.
-
Schat het aantal Nederlanders in 1986 met behulp van de grafiek.
-
Denk je dat het antwoord bij a betrouwbaar is? Geef een toelichting.
-
Schat het aantal Nederlanders in 1945 met behulp van de grafiek.
Waarom kan deze uitkomst wel eens erg onbetrouwbaar zijn?
-
Schat het aantal Nederlanders in 2020. Leg uit hoe je te werk bent gegaan.
-
Gebruik de grafieken van de watertemperatuur uit Voorbeeld 2.
-
Hoe warm is het water om 11:00 uur op 3 m diepte?
-
Waarom gaat loopt de grafiek bij een diepte van 0 m tussen 6 en 10 uur steiler dan de andere twee grafieken?
-
En waarom is dit na 10 uur niet meer het geval?
-
Kun je iets zeggen over de grafieken na 14 uur?
-
In Voorbeeld 3 vind je de grafiek van de waterstanden bij Harlingen.
Dit is een periodieke grafiek.
-
Voorspel de waterstand om 14:00 uur van de volgende dag.
Bekijk in het voorbeeld hoe je dat kunt doen.
-
Hoe hoog is de waterstand twee dagen later om 14:00?
-
Waarom zijn deze antwoorden toch alleen maar schattingen?
Verwerken
-
Bekijk nog eens de schoolartsenkaart voor meisjes.
De P50-lijn geeft de lengte aan van een gemiddeld meisje.
-
Schat door grafisch interpoleren de lengte van een gemiddeld meisje van 15 jaar en 3 maanden.
-
Marleen van Straaten is op haar dertiende verjaardag 164 cm en op haar veertiende verjaardag is ze 168 cm.
Voorspel hoe lang ze op haar twintigste zal zijn door gebruik te maken van de groeigrafieken.
-
Waarom is extrapoleren met behulp van een rechte lijn door beide punten hier onzinnig?
-
Voorspel hoe zwaar Marleen op haar twintigste zal zijn.
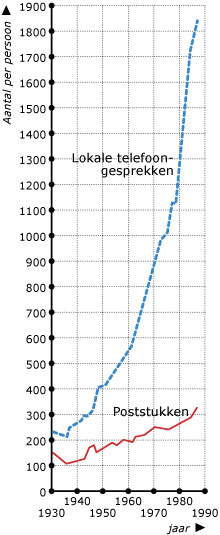 In de grafiek hiernaast staat het aantal lokale telefoongesprekken per persoon per
jaar uitgezet tegen het aantal poststukken per persoon per jaar in de Verenigde
Staten.
In de grafiek hiernaast staat het aantal lokale telefoongesprekken per persoon per
jaar uitgezet tegen het aantal poststukken per persoon per jaar in de Verenigde
Staten.
-
Na een aanvankelijke daling stijgt de grafiek van het aantal lokale telefoongesprekken per persoon per jaar voortdurend, behalve in twee jaren. Welke jaren zijn dat?
-
Is het totaal aantal lokale telefoongesprekken die jaren ook niet gestegen?
Verklaar je antwoord.
-
In welke periodes daalde het aantal poststukken per persoon per jaar?
-
Bepaal door extrapoleren het aantal lokale telefoongesprekken en het aantal poststukken per persoon per jaar in het jaar 2000 in de Verenigde Staten. Licht toe hoe je te werk gaat.
-
De tabel geeft het aantal werkelozen in een bepaalde stad weer. De aantallen werkelozen zijn afgerond op honderdtallen.
| tijd | mrt'04 | mei'04 | jul'04 | sep'04 | nov'04 | jan'05 | mrt'05 | mei'05 | jul'05 | sep'05 |
| aantal | 10700 | 11400 | 11100 | 10300 | 10000 | 10700 | 11900 | 12600 | 12300 | 11500 |
-
Maak een grafiek van deze werkloosheidscijfers.
-
Hoe kun je aan de grafiek zien dat er bij werkloosheid sprake is van seizoensinvloeden?
-
Ga er van uit dat deze trend zich voortzet. Voorspel nu het aantal werklozen in deze stad in januari 2014.
-
Hoeveel werklozen waren er volgens deze trend in maart 2008?
-
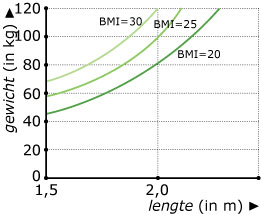
De Body Mass Index (BMI) geeft aan of mensen van boven de 16 jaar op hun juiste
gewicht zitten (20 < BMI ≤ 25), matig overgewicht hebben (25 < BMI ≤ 30), of te zwaar (BMI > 30) of te licht (BMI ≤ 20) zijn.
Met deze grafieken kun je de BMI bepalen.
-
Schat de BMI van iemand die 18 jaar is, 1,90 m lang is en 90 kg weegt.
-
Hoe zwaar moet iemand van meer dan 16 jaar zijn als hij 1,80 m lang is en een gezond gewicht wil hebben?
Geef de ondergrens en de bovengrens.
-
Schets de grafiek die hoort bij een BMI van 23.
-
Waarom gelden deze grafieken voor de BMI alleen voor mensen boven de 16 jaar, denk je?
-
Als je 1,80 m lang bent, hangt je BMI alleen af van je gewicht.
Teken de grafiek van de BMI afhankelijk van het gewicht.
Testen
-
Deze tabel geeft het aantal inwoners en het aantal woningen in een bepaalde gemeente weer.
| jaar |
1980 |
1990 |
1995 |
2000 |
| aantal inwoners |
11220 |
13910 |
14730 |
14990 |
| aantal woningen |
2800 |
4000 |
4400 |
4800 |
-
Maak een grafiek van het aantal inwoners in de periode van 1980 - 2000.
Maak ook een grafiek van het aantal woningen in die periode.
-
Bereken door interpoleren het aantal inwoners in 1985 en het aantal inwoners in 1998.
-
Bereken door interpoleren het aantal woningen in die jaren.
-
Bereken door extrapoleren het aantal inwoners in 2008 en het aantal woningen in 2008.
-
Maak een grafiek van het aantal inwoners per woning in de periode van 1980 - 2000. Wat valt op?
-
Bereken door extrapoleren het aantal inwoners per woning in 2008.
Dat kan op twee manieren; ga na of de antwoorden met elkaar overeen komen.
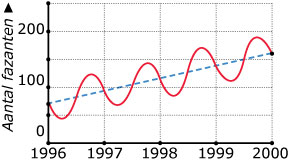 In deze grafiek is sprake van een duidelijke trend. Het aantal fazanten in dit
gebied neemt gestadig toe.
In deze grafiek is sprake van een duidelijke trend. Het aantal fazanten in dit
gebied neemt gestadig toe.
-
Waaraan kun je zien dat het aantal fazanten onderhevig is aan seizoensinvloeden?
-
Waaruit blijkt de trend?
-
Bepaal het aantal fazanten in juni 2006 als deze trend zich voortzet.
Leg uit hoe je te werk gaat










 In de grafiek hiernaast staat het aantal lokale telefoongesprekken per persoon per
jaar uitgezet tegen het aantal poststukken per persoon per jaar in de Verenigde
Staten.
In de grafiek hiernaast staat het aantal lokale telefoongesprekken per persoon per
jaar uitgezet tegen het aantal poststukken per persoon per jaar in de Verenigde
Staten.

 In deze grafiek is sprake van een duidelijke trend. Het aantal fazanten in dit
gebied neemt gestadig toe.
In deze grafiek is sprake van een duidelijke trend. Het aantal fazanten in dit
gebied neemt gestadig toe.