
Grafieken
Inleiding
Het woord "grafiek" wordt wel voor elke soort getekende voorstelling van gegevens gebruikt.
Hier gaat het alleen om grafieken die horen bij tabellen met twee variabelen: bijvoorbeeld van het aantal mensen in een bepaalde gemeente afhankelijk van de tijd (het jaartal). Een grafiek laat dan het verloop van de bevolking van die gemeente heel duidelijk zien, duidelijker vaak dan een tabel.
Er zijn verschillende soorten grafieken, belangrijk is welke soort grafiek je wanneer gebruikt. En verder hebben grafieken eigenschappen zoals dalend en stijgend. Die moet je leren herkennen...
Je leert nu:
- grafieken gebruiken om gegevens overzichtelijk te presenteren;
- soorten grafieken onderscheiden;
- eigenschappen van grafieken herkennen.
Je kunt al:
- een grafiek tekenen bij een tabel;
- werken met procenten.

Verkennen
Via internet kun je grafieken zoeken. Ga naar Google en zoek afbeeldingen bij het trefwoord "grafiek".
Bekijk de figuren die je nu voor je neus krijgt.
> Meld bij elke figuur of het om een grafiek gaat zoals in de inleiding bedoeld of om een (staaf-, lijn-, of cirkel-)diagram of om nog wat anders...
> Probeer bij elke grafiek vast te stellen waar hij over gaat, bijvoorbeeld tussen welke variabelen hij het verband beschrijft.
Uitleg
Op de website www.getij.nl van het Ministerie van Verkeer en Waterstaat vind je bij "Getijvoorspellingen" de waterstanden voor de komende dagen op verschillende locaties in Nederland en op de Noordzee.
Je ziet er grafieken zoals deze.
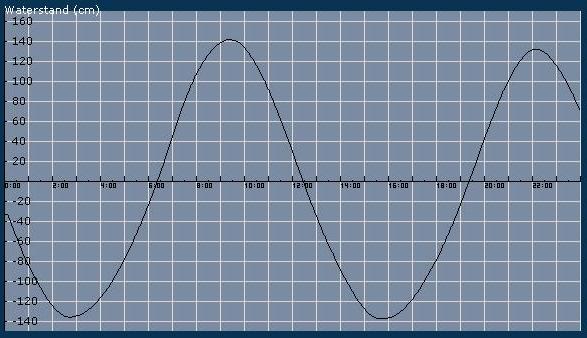
Er is sprake van twee variabelen: de hoogte van het water t.o.v. NAP (Normaal Amsterdams Peil) is uitgezet tegen de tijd in uren. Op de verticale as vind je de variabele waterstand (in cm), op de horizontale as staat de variabele tijd (in uren).
De grafiek stijgt en daalt afwisselend. De waterstand is
- stijgend als hij toeneemt met de tijd en
- dalend als hij afneemt met de tijd;
- maximaal als hij overgaat van stijgend naar dalend (hoogwater of vloed) en
- minimaal als hij overgaat van dalend in stijgend (laagwater of eb).
Zoek steeds de bijpassende tijden in de grafiek op.
Omdat de waterstand voortdurend verandert is er sprake van een vloeiend lopende grafiek.
De waterstanden variëren tussen hoogwater en laagwater met een periode van ongeveer 6,25 uur. Tussen twee opeenvolgende tijdstippen van hoogwater zit ongeveer 12,5 uur en hetzelfde geldt voor twee opeenvolgende tijdstippen van laagwater. Zo'n grafiek die zichzelf (ongeveer) herhaalt noem je periodiek.
‡
Opgaven
-
Bekijk de grafiek van de waterstanden in de Uitleg.
-
Tussen welke tijdstippen is de grafiek stijgend?
-
Geef de tijden waarop de waterstand maximaal is (hoogwater). Hoe hoog staat het water dan?
-
Geef ook de tijden waarop de waterstand minimaal is (laagwater). Hoe hoog staat het water dan?
-
De grafiek van de waterstanden wordt in de Uitleg periodiek genoemd.
-
Om de hoeveel tijd herhaalt zich de waterstand (ongeveer)?
-
Stel dat deze grafiek geldt voor 10 mei 2008. Op welke tijdstippen was het dan hoogwater op 12 mei 2008?
-
Kun je bedenken waarom deze grafiek niet zuiver periodiek zal zijn?
Theorie
Bij een tabel met twee variabelen kun je een grafiek maken (bijvoorbeeld m.b.v. Excel).
Bijvoorbeeld bij een CBS-tabel van de Nederlandse bevolking komen de twee variabelen tijd (jaartal) en aantal Nederlanders (× 1000) voor. Hierbij hangt aantal Nederlanders af van tijd. Je maakt er daarom een grafiek bij met op de horizontale as de variabele tijd en op de verticale as de afhankelijk variabele aantal Nederlanders.
Bij de assen zet je de namen van die variabelen als bijschriften. Ook gebruik je maatstreepjes met getallen.
Laat je die weg, dan weet je de betekenis van de as en/of de gebruikte eenheid niet.
Soms krijgt een grafiek nog een grafiektitel mee.
Er zijn verschillende soorten grafieken
- bij een lijngrafiek verbind je de punten die bij de tabel horen met dunne lijnstukjes omdat je de tussenwaarden niet weet;
- bij een vloeiende grafiek verbind je de punten die bij de tabel horen met een kromme lijn omdat je aan kunt nemen of weet dat de tussenwaarden zonder grote sprongen toenemen of afnemen;
- bij een trapgrafiek ga je er van uit dat de afhankelijk variabele sprongsgewijs verandert.
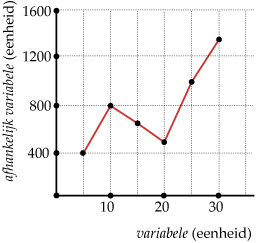
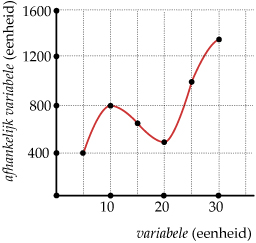
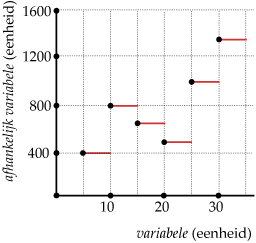
Grafieken hebben bepaalde eigenschappen...
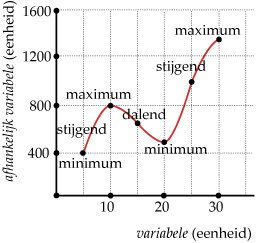
Een (vloeiende) grafiek is
- stijgend als de afhankelijk variabele toeneemt;
- dalend als de afhankelijk variabele afneemt;
De grafiek heeft
- een maximum als hij overgaat van stijgend naar dalend;
- een minimum als hij overgaat van dalend in stijgend.
Ook in randpunten zit vaak een maximum of een minimum.
Je noemt de maxima en de minima wel extremen of uiterste waarden.
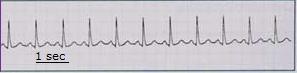
Soms varieert de afhankelijk variabele met een vaste periode.
Zo'n grafiek die zichzelf (ongeveer) herhaalt noem je periodiek.
Deze grafiek van een normale hartslag is daarvan een voorbeeld. De periode is hier ongeveer 0,8 seconden. Dat betekent een frequentie van 75 hartslagen per minuut.
‡
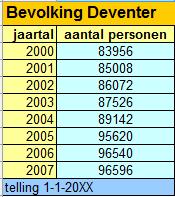
Voorbeeld 1
Hier zie je een tabel van de bevolking van Deventer.
Het aantal mensen hangt af van de tijd (jaartal).
Maak een bijpassende grafiek. Neem aantal mensen in honderdtallen.
Welke soort grafiek maak je en waarom?
In de loop van 2004 is de gemeente Deventer uitgebreid. Hoe zie je dat in de grafiek?
Antwoord
Maak eerst een nieuwe tabel met aantal personen in honderdtallen.
Zet dan de punten uit die nieuwe tabel in een assenstelsel en verbind ze.
Je kunt daarvoor bijvoorbeeld Excel inschakelen.
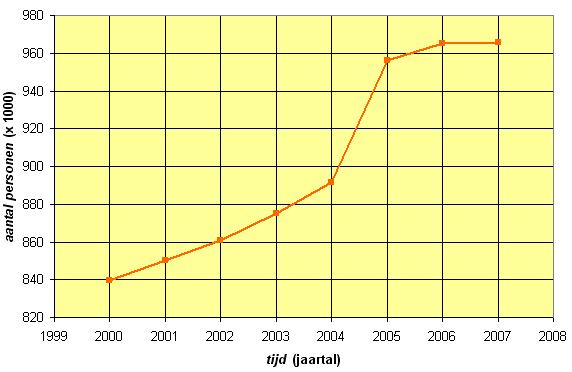
Er is gekozen voor een lijngrafiek omdat de tussenwaarde niet bekend zijn. Hier past ook wel een vloeiende grafiek bij, want er zullen waarschijnlijk geen rare uitschieters zijn gedurende een jaar. Zelfs een trapgrafiek is te verdedigen, je baseert je dan uitsluitend op de tellingen van 1-1-20XX en neemt dat als waarde voor een heel jaar.
De uitbreiding van de gemeente is terug te vinden in de snelle stijging tussen de punten bij 2004 en 2005. Die stijging heeft in de loop van 2004 plaatsgevonden, kennelijk nam het aantal personen toen sneller toe vanwege de gebiedsuitbreiding.
‡
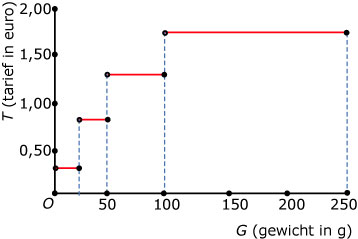
Voorbeeld 2
De TPG-tarieven voor de brievenbuspost binnenland zijn in 2007:
- van 0 tot en met 20 gram: € 0,44
- van 20 tot en met 50 gram: € 0,88
- van 50 tot en met 100 gram: € 1,32
- van 100 tot en met 250 gram: € 1,76
Het tarief T is is afhankelijk van het gewicht g.
Maak een bijpassende grafiek.
Antwoord
De bijpassende grafiek moet nu een trapgrafiek zijn. Je ziet hem hier. Let goed op de open rondjes. Die zorgen er voor dat er overal precies één uitkomst is. Bijvoorbeeld bij een brief van 50 gram betaal je 88 cent en niet € 1,32.
Een brief van meer dan 250 gram bestaat kennelijk niet, dan is het een pakket.
‡
Voorbeeld 3
Deze grafiek geeft de snelheid aan van iemand die vanaf huis met zijn scooter naar school gaat.
Je ziet dat zij de eerste halve minuut gemiddeld 20 km/h (km per uur) rijdt.
Hoeveel km legt zij die eerste halve minuut af?
Teken een grafiek van de afgelegde afstand afhankelijk van de tijd.
Antwoord
De eerste halve minuut rijdt zij gemiddeld 20 km/h = `1/3` km/min. In die halve minuut legt ze `1/6` km af.
Daarna rijdt ze 3,5 minuten met 40 km/h = `2/3` km/min. Ze legt dan elke halve minuut `1/3` km af. Nu kun je een tabel maken voor de eerste vier minuten.
De volgende halve minuut rijdt ze gemiddeld weer met 20 km/h = `1/3` km/min. En dan staat ze een minuut stil.
Zo kun je je tabel en je grafiek voortzetten en afmaken.
Ga na, dat er in totaal `4 2/3` km wordt afgelegd.
‡
Opgaven
-
Bekijk de Theorie en Voorbeeld 1. Je ziet hier een tabel van het aantal Nederlanders in de loop van de jaren. Deze tabel is afkomstig van de website van het C.B.S.
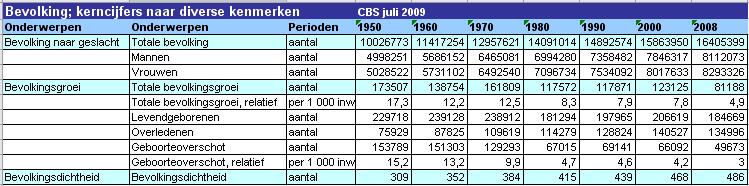
-
Maak een grafiek van het aantal inwoners van Nederland in de loop van de jaren.
-
Welke twee variabelen heb je tegen elkaar uitgezet? Welke van beide variabelen is de afhankelijk variabele?
Hoe zie je dat aan de grafiek?
-
Waarom kun je eigenlijk geen vloeiende grafiek maken?
-
Wat is het voordeel van een grafiek boven een tabel? Zijn er ook nadelen?
-
Gebruik de tabel van de vorige opgave. Je bekijkt nu de rijen "Levendgeborenen", "Overledenen" en "Geboorteoverschot".
-
Teken de drie grafieken van deze variabelen uitgezet tegen de tijd (in jaren) in één figuur.
-
Waarom noem je de grafiek van "Geboorteoverschot" wel de verschilgrafiek van de andere twee?
-
In welke periode is de grafiek van "Geboorteoverschot" stijgend?
-
Wat betekent het dat het geboorteoverschot in Nederland dalend is?
-
In Voorbeeld 2 vind je de grafiek van de TPG-tarieven voor brievenbuspost in 2007.
-
Hoe zwaar is brievenbuspost op zijn hoogst?
-
Waarom moet de grafiek een trapgrafiek zijn?
-
Hoeveel betaal je voor een brief van 100 gram?
-
Hoe zwaar is een brief als er 88 cent aan postzegels op moet?
-
Wat kun je beter doen: twee brieven van 45 gram die naar hetzelfde adres moeten afzonderlijk versturen of samen (als één brief) versturen?
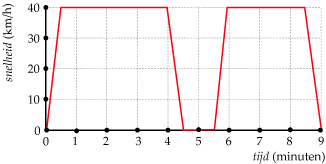
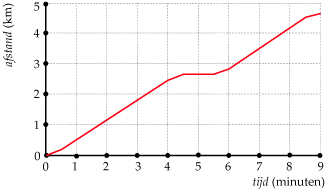
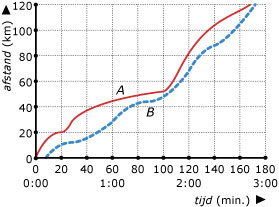 Je ziet hier de grafieken van twee wielrenners die een wedstrijd over 120 km
rijden. Het is een individuele tijdrit, dus ze starten na elkaar. Bekijk eventueel eerst Voorbeeld 3.
Je ziet hier de grafieken van twee wielrenners die een wedstrijd over 120 km
rijden. Het is een individuele tijdrit, dus ze starten na elkaar. Bekijk eventueel eerst Voorbeeld 3.
-
Welke van beide wielrenners startte het snelst? Hoe zie je dat aan de grafiek?
-
Hoeveel bedroeg de gemiddelde snelheid van renner A het eerste uur ongeveer?
En gerekend over de gehele rit?
-
Welk stuk van de route gaan ze bergop? Licht je antwoord toe.
-
Wie van beiden is de beste klimmer?
-
Op welk moment fietsen beiden even snel?
-
Wie wint de tijdrit?
-
Waarom hebben deze grafieken geen dalende stukken?
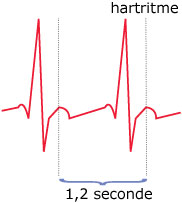 In de Theorie kom je ook een periodieke grafiek tegen.
Op de intensive care van een ziekenhuis bewaakt men met hartbewakingsapparatuur de hartfunctie van patiënten.
Hier zie je een grafische weergave van de hartslag van een patiënt.
De hartslag van een mens wordt gewoonlijk uitgedrukt in het aantal slagen per minuut.
In de Theorie kom je ook een periodieke grafiek tegen.
Op de intensive care van een ziekenhuis bewaakt men met hartbewakingsapparatuur de hartfunctie van patiënten.
Hier zie je een grafische weergave van de hartslag van een patiënt.
De hartslag van een mens wordt gewoonlijk uitgedrukt in het aantal slagen per minuut.
-
Wat is het aantal hartslagen van deze patiënt per minuut?
-
Hoe groot is de hartslagfrequentie per seconde?
-
De grafiek herhaalt zich steeds. Hoe groot is de periode van dit periodieke verschijnsel?
-
Iemand die een zware lichamelijke inspanning heeft geleverd, heeft kort daarna meestal een verhoogde hartslagfrequentie.
Hoe zal de grafiek van deze persoon eruit zien na een zware lichamelijke inspanning?
Verwerken
Dodelijke ongelukken
als gevolg van brand
in de U.S.A. |
| jaar | aantal
doden | aantal doden
per 100000
inwoners |
| 1950 | 6405 | 4,2 |
| 1952 | 6922 | 4,4 |
| 1954 | 6003 | 3,7 |
| 1956 | 6405 | 3,8 |
| 1958 | 7291 | 4,2 |
| 1960 | 7645 | 4,2 |
| 1962 | 7534 | 4,0 |
| 1964 | 7379 | 3,8 |
| 1966 | 8084 | 4,1 |
| 1968 | 7335 | 3,7 |
| 1970 | 6718 | 3,3 |
| 1972 | 6714 | 3,2 |
| 1974 | 6236 | 2,9 |
| 1976 | 7480 | 3,5 |
| 1978 | 7440 | 3,4 |
| 1979 | 6245 | 2,8 |
| 1980 | 5765 | 2,6 |
| 1981 | 5860 | 2,6 |
| 1982 | 5325 | 2,3 |
-
De tabel geeft het aantal dodelijke ongelukken ten gevolge van branden in de periode 1950 t/m 1982 in de
Verenigde Staten weer.
-
Teken een geschikte grafiek bij de eerste twee kolommen. Leg uit welke soort grafiek je hebt gekozen en waarom.
-
Welke variabele is de afhankelijk variabele?
-
Kun je een conclusie trekken omtrent het aantal doden ten gevolge van brand?
Waar heb je dan meer aan, de tabel of de grafiek?
-
Waarom is ook de derde kolom nodig om te concluderen dat maatregelen voor brandpreventie na 1980 succes begonnen af te werpen?
-
Schat met behulp van deze tabel het aantal inwoners van de Verenigde Staten in 1982.
-
Download en print de schoolartsenkaart voor meisjes. Een uitdrukking als P10 bij een grafiek op deze kaart betekent dat 100% van de meisjes daar onder zit.
-
Welke twee variabelen worden er in het onderste deel van deze kaart tegen elkaar uitgezet?
-
Welke twee variabelen worden er in het bovenste deel van de kaart tegen elkaar uitgezet?
-
Waarom staan er op deze kaart al grafieken voorgedrukt? Welke betekenis hebben ze?
-
Hoe kun je met behulp van deze schoolartsenkaart de lengte en het gewicht voorspellen van een vrouw van 20 jaar?
-
Je ziet in de tabel de gegevens van Marleen van Straaten. Haar lengte is steeds op haar verjaardag gemeten.
Teken haar twee groeigrafieken op de schoolartsenkaart.
-
Is Marleen lang voor haar leeftijd? En hoe zit het met haar gewicht?
-
Als je een glazen vaas onder een gelijkmatig stromende kraan houdt, zie je de
waterspiegel in de vaas stijgen. Je ziet hieronder vier vazen met dezelfde hoogte,
maar met een verschillende vorm. Verder zie je vier grafieken waarin
de waterhoogte `h` (in cm) is uitgezet tegen de tijd `t` (in seconden).
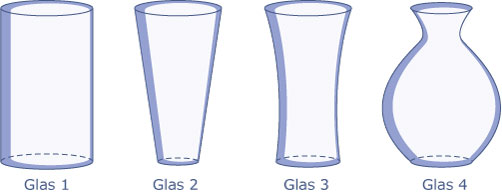
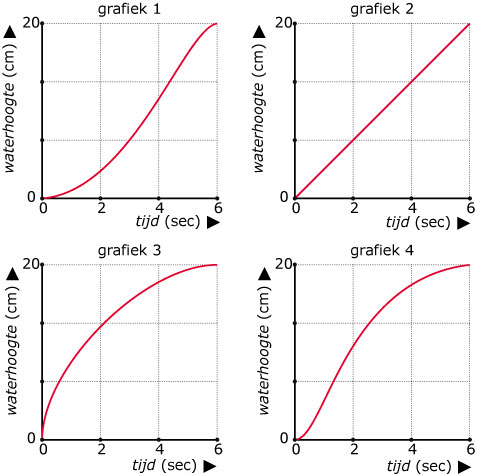
-
Waarom zijn dit allemaal vloeiend lopende grafieken?
-
Welke grafiek hoort bij welke vaas?
-
Teken de grafieken van `h` afhankelijk van `t` als het water twee keer zo snel stroomt.
-
De hoeveelheid kooldioxide (CO2) en de hoeveelheid zuurstof in de lucht (O2) worden
onder andere in balans gehouden doordat de planten op Aarde kooldioxide omzetten in zuurstof. Deze grafieken laten dat zien.
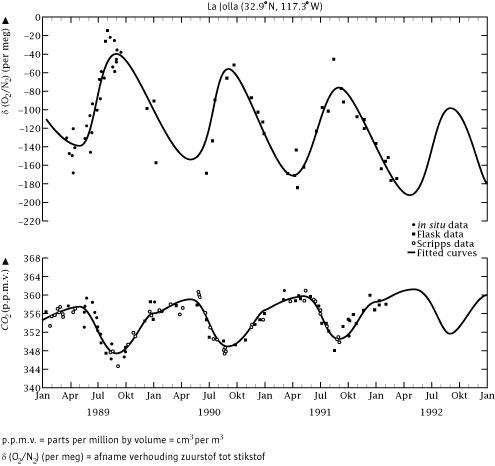
- Hoe groot is de periode van beide grafieken?
- Waarom daalt de hoeveelheid CO2 in de atmosfeer in de periode mei t/m augustus?
-
Hoeveel cm3 CO2 zat er in 1990 per m3 minimaal in de atmosfeer?
En hoeveel maximaal?
-
De maxima van de bovenste grafiek komen overeen met de minima van de onderste grafiek en andersom. Verklaar dat.
-
In de grafiek is een dalende tendens zichtbaar voor wat betreft de verhouding zuurstof/stikstof in de atmosfeer.
Teken een trendlijn die dit weergeeft.
-
Teken ook een trendlijn voor de kooldioxidegrafiek. Hangen beide trendlijnen met elkaar samen?
-
Voorspel het gehalte kooldioxide in januari 2010 als deze trend zich voortzet.
Testen
-
In deze tabel vind je de levensverwachting van mannen en vrouwen bij hun geboorte in de tweede helft van de vorige eeuw.
| jaar |
1950 |
1960 |
1970 |
1980 |
1990 |
| man |
70,0 |
71,0 |
71,0 |
72,2 |
72,8 |
| vrouw |
72,5 |
75,5 |
76,9 |
77,8 |
79,5 |
-
Teken de twee bijbehorende grafieken in één figuur.
-
Hoe heb je de punten die horen bij waarden uit de tabel met elkaar verbonden? Motiveer je keuze.
-
In een bepaalde periode is het verschil tussen de levensverwachting bij mannen en bij vrouwen sterk toegenomen.
In welke periode was dat?
-
Kun je redenen geven voor de toenemende levensverwachting bij vrouwen?
-
Waarom veranderde de levensverwachting bij mannen in de periode 1950 - 1970 niet veel en die van vrouwen wel, denk je?
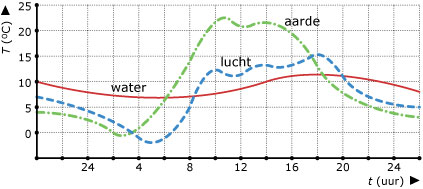 Deze grafieken geven het temperatuurverloop van het aardoppervlak, de lucht
en het water op een zonnige voorjaardag in Nederland weer.
Deze grafieken geven het temperatuurverloop van het aardoppervlak, de lucht
en het water op een zonnige voorjaardag in Nederland weer.
-
Leg uit hoe je aan de grafieken kunt zien dat het om een zonnige voorjaarsdag in Nederland gaat.
-
Hoeveel bedroeg de maximale temperatuur van de atmosfeer die dag? Op welk tijdstip werd die temperatuur bereikt?
-
Op bepaalde delen van de dag was het die dag zo bewolkt dat de temperatuur van de lucht daalde.
Welke delen van de dag waren dat?
-
Wat warmt het snelst op: aarde, lucht of water? Hoe zie je dat aan de grafieken?
-
Wat houdt de temperatuur het beste vast: aarde, lucht of water? Hoe zie je dat aan de grafieken?
-
De volgende dag is het dicht bewolkt. Maak een schets van het verloop van de drie grafieken op die dag.
-
Leg uit waarom deze temperatuurgrafieken wel een vaste periode hebben, maar er toch geen sprake is van een zuiver periodiek verschijnsel.
-
Is er sprake van trend?














 Je ziet hier de grafieken van twee wielrenners die een wedstrijd over 120 km
rijden. Het is een individuele tijdrit, dus ze starten na elkaar. Bekijk eventueel eerst Voorbeeld 3.
Je ziet hier de grafieken van twee wielrenners die een wedstrijd over 120 km
rijden. Het is een individuele tijdrit, dus ze starten na elkaar. Bekijk eventueel eerst Voorbeeld 3.
 In de Theorie kom je ook een periodieke grafiek tegen.
Op de intensive care van een ziekenhuis bewaakt men met hartbewakingsapparatuur de hartfunctie van patiënten.
Hier zie je een grafische weergave van de hartslag van een patiënt.
De hartslag van een mens wordt gewoonlijk uitgedrukt in het aantal slagen per minuut.
In de Theorie kom je ook een periodieke grafiek tegen.
Op de intensive care van een ziekenhuis bewaakt men met hartbewakingsapparatuur de hartfunctie van patiënten.
Hier zie je een grafische weergave van de hartslag van een patiënt.
De hartslag van een mens wordt gewoonlijk uitgedrukt in het aantal slagen per minuut.



 Deze grafieken geven het temperatuurverloop van het aardoppervlak, de lucht
en het water op een zonnige voorjaardag in Nederland weer.
Deze grafieken geven het temperatuurverloop van het aardoppervlak, de lucht
en het water op een zonnige voorjaardag in Nederland weer.