Procenten

Inleiding

In veel tabellen komen procenten voor. "Pour cent" betekent per honderd, dus één van elke honderd, dus 1/100 deel. Met procenten rekenen is daarom rekenen met honderdsten: 45% = `45/100 = 0,45`.
En 45% ergens van uitrekenen komt neer op vermenigvuldigen met 0,45.
Het werken met procenten is al heel oud, zelfs de Oude Grieken kenden al het werken "per honderd". Het teken voor procenten is echter nog niet heel oud en vermoedelijk ontstaan uit de afkorting p.c. (pour cent).

Je leert nu:

opnieuw rekenen met procenten;
werken met indexcijers.

Je kunt al:

werken met tabellen, tabellen maken en interpreteren;
werken met procenten in eenvoudige situaties.

Verkennen

Een zelfstandige zonder personeel is iemand die een bedrijf heeft en zijn diensten of zijn artikelen te koop aanbiedt, maar geen personeel heeft. Zo iemand hoeft geen BTW (belasting toegevoegde waarde) te betalen over zaken die hij voor zijn bedrijfsuitvoering nodig heeft.
Stel hij koopt een laptop om de boekhouding mee te doen voor € 745,00 inclusief BTW.
Het BTW-tarief daarop is 19% van de prijs van deze laptop.

> Hoeveel bedraagt die prijs dus?

Uitleg

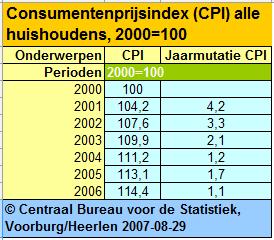
De consumenten prijsindex alle huishoudens (CPI) die het CBS berekent geeft de gemiddelde prijsverandering weer van goederen en diensten die huishoudens aanschaffen. De CPI is een voorbeeld van het werken met procenten.
Het jaar 2000 is het indexjaar, de totale prijs van de 1600 artikelen en diensten waarvan het CBS de prijsontwikkeling volgt wordt aan het begin van het jaar 2000 op 100 gesteld, zeg maar 100% genoemd. Vervolgens wordt berekend hoeveel die totale prijs aan het begin van een ander jaar is en uitgerekend met hoeveel procent hij is gestegen of gedaald t.o.v. de prijs in 2000. Dat is het indexcijfer voor dat jaar.

Je ziet dat voor 2006 het indexcijfer 114,4 bedraagt. De prijzen zijn dus gemiddeld voor de consument met 14,4% gestegen t.o.v. die in 2000.

De prijsstijging t.o.v. 2005 reken je zo uit: de toename is `114,4 - 113,1 = 1,3` en dat is
het `(1,3)/(113,1)` deel van 113,1.
Uit deze deling komt ongeveer 0,011 en dat is 1,1%.
De prijsstijging t.o.v. 2005 is daarom 1,1%. In de tabel heet dit de jaarmutatie.

De prijsstijging t.o.v. 2004 is `(114,1 - 111,2)/(111,2) ~~ 0,0288 ~~ 2,9`%.

‡

Opgaven

Bekijk de tabel van de consumenten prijsindex in de Uitleg.
1. Welk jaar is het indexjaar? En wat betekent dat?
2. Hoeveel bedraagt het indexcijfer voor 2004? Met hoeveel zijn de prijzen dus gestegen ten opzicht van 2000?
3. Met hoeveel zijn de prijzen in 2004 gestegen ten opzichte van 2003?
4. Met hoeveel zijn de prijzen in 2004 gestegen ten opzichte van 2002?

Stel je voor dat in 2007 de jaarmutatie van de consumenten prijsindex 1,6 bedroeg.
1. Welk indexcijfer krijgt 2007 dan?
2. Met hoeveel procent zijn de prijzen in 2007 gestegen ten opzichte van het indexjaar 2000?

Theorie

Het Franse 'pour cent' betekent 'per honderd', dus 1 procent is 1 per 100.
Dat wordt dus `1/100` deel van het totaal. Je schrijft: 1% = `1/100 = 0,01`.
En 12% van 500 is `12/100` deel van 500. Dat is 0,12 × 500 = 60.

Hoeveel procent is 24 van 65?
Antwoord: `24/60 ~~ 0,369 = 36,9`%.

Het getal 24 neemt toe tot 27, met hoeveel procent is dat?
Antwoord: `(27 - 24)/24 = 0,125 = 12,5`%.

Het getal 24 neemt toe met 6%, hoeveel wordt het?
Antwoord: 24 × 1,06 = 25,44.

Het getal 24 neemt af met 6%, hoeveel wordt het?
Antwoord: 24 × 0,94 = 22,56.

Het getal 24 is 6% van het geheel, hoeveel is dat geheel?
Antwoord: 0,06 × geheel = 24, dus het geheel is `24/(0,06) = 400`.

Een getal neemt met 6% toe tot 60, welk getal is dat?
Antwoord: getal × 1,06 = 60, dus het getal is `60/(1,06) ~~ 56,60`.

‡

Voorbeeld 1

Een winkelier doet zijn oude voorraad in de uitverkoop.
Hij geeft 40% korting op de prijs ex.BTW. Het geldende BTW-tarief is 19%.
De stereoset die jij wilt hebben kost nu € 250,00.
Hoeveel bedroeg de oorspronkelijke prijs (ex.BTW)?

Antwoord

Noem de oorspronkelijke prijs p, dan is de prijs met 40% korting: p × 0,6.
Daar komt 19% BTW bij, de prijs wordt dan p × 0,6 × 1,19 = 250 euro.

Dus moet je 250 delen door 1,19 en vervolgens door 0,6.
De oorspronkelijk prijs was € 350,14.

‡

Voorbeeld 2

Hier zie je de ontwikkeling van de consumenten prijsindex vanaf het jaar 2000.
Dit jaar is het indexjaar, de prijs van een artikel is in dat jaar op 100% gesteld.

In 2006 kostte een brood € 1,50. Hoeveel kostte dit brood in 2000?
In 2006 kostte een brood € 1,50. Hoeveel kostte dit brood in 2003?
De jaarmutatie geeft de procentuele toename t.o.v. het voorgaande jaar weer weer. Als bij 2000 een jaarmutatie van 5,6 zou horen, wat is dan het indexcijfer van 1999?

Antwoord

Stel: prijs in 2000 is a, dan 1,144 × a = 1,50.
Dus a = `(1,50)/(1,144) ~~ 1,31`. De prijs in 2000 was dus 1,31 euro.
Stel: prijs in 2003 is b, dan `(114,4)/(109,9)` × b = 1,50.
Dus b = `(1,50)/(114,4) ~~ 1,44`. De prijs in 2003 was dus 1,44 euro.
Als i het indexcijfer van 1999 is, dan is 1,056 – i = 100.
En dus is i = `(100)/(1,056) ~~ 94,7`.

‡

Voorbeeld 3

De Gasunie is de Nederlandse producent van aardgas.
Ooit was al ons gas om te koken en het huis te verwarmen afkomstig van de Gasunie, maar tegenwoordig wordt ook gas uit het buitenland gekocht. In 2005 bedroeg de binnenlandse afzet via de Gasunie 38,7 miljard m³ en dat was 63% van het binnenlands verbruik. Zie ook www.energie.nl.
Hoeveel aardgas voor binnenlands verbruik kwam van andere leveranciers?

Antwoord

Noem de totale hoeveelheid aardgas A, dan is 0,63 × A = 38,7 mld m³.
Dus A = `(38,7)/(0,63) ~~ 61,4` mld m³.

De hoeveelheid aardgas voor binnenlands van andere leveranciers was dus 61,4 – 38,7 = 22,7 mld m³.

‡

Opgaven

Bekijk de Theorie. Schrijf als percentage:
1. 0,25 = ...
2. 0,375 = ...
3. 0,001 = ...
4. 3,14 = ...

Bereken:
1. 24% van 150
2. 11% van 2150
3. 3,4% van 15600
4. 0,4% van 530

Hoeveel procent is
1. `1/4` deel
2. `1/8` deel
3. 5 van de 40
4. `12/50` deel
5. 8 van de 25
6. `11/500` deel

Waarom is 1/3 deel niet precies 33%? Is het meer of minder dan 33%?

Bereken telkens de nieuwe prijs, of het nieuwe bedrag.
1. Je koopt een fiets van € 650,= met 12,5% korting.
2. De contributie van de tafeltennisclub is € 120,= per jaar. Hij wordt met 5% verhoogd.
3. Sinds 1960 is de prijs van de benzine met ongeveer 110% gestegen. Toen kostte 1 L benzine € 0,54.

Je haalt van een bedrag eerst 10% af en doet er dan weer 10% van het nieuwe bedrag bij.
Laat met een berekening zien of je weer hetzelfde bedrag hebt gekregen.

Bekijk Voorbeeld 1 over berekening van de BTW.
1. De BTW op een fiets die € 650,00 kost ex.BTW (dus zonder BTW) is 19% van de prijs. Hoeveel betaal je voor deze fiets inclusief BTW?
2. Je koopt een nieuw I-Pod Classic met 25% korting voor € 185,00. Hoeveel kostte deze I-Pod oorspronkelijk ex.BTW?

In Voorbeeld 2 wordt opnieuw met indexcijfers gerekend.
1. Hoeveel betaal je in 2006 voor een pak melk dat in 2000 nog € 0,80 kostte?
2. Hoeveel betaal je in 2006 voor een pak melk als dit in 2004 nog € 1,05 kostte?
3. Als 2004 het indexjaar wordt, welke prijsindex krijgt 2006 dan? En 2000?

In Voorbeeld 3 reken je vanuit een gegeven percentage het oorspronkelijke bedrag weer terug.
1. Als 85% van een bepaald bedrag € 70,00 is, hoeveel is dan dit bedrag?
2. Als je 20% korting krijgt en je moet nog € 55,00 betalen, hoeveel was dan de oorspronkelijke prijs?

Verwerken

Marianne is met haar vriendin Anneke aan het winkelen. Op een gegeven moment komen ze langs een winkel met enorme aanbiedingen die ze meteen binnenstormen.
1. Marianne ziet een trui van € 49,98. Wat gaat die trui kosten met deze korting?
2. Anneke koopt twee spijkerbroeken met winkelprijs € 51,75. Wat betaalt ze daarvoor?
3. Marianne ziet een blouse waarop 20% korting staat. De winkelprijs is € 33,50 en ze moet er € 27,00 voor betalen. Klopt het kortingspercentage wel?

Je hebt op 1 januari 2009 een bedrag van € 1000,= op een rekening bij een bepaalde bank gezet. Je doet er verder niets mee, je krijgt alleen jaarlijks 3,5% rente van de bank.
1. Hoeveel geld heb je dan op 1 januari 2010?
2. En hoeveel op 1 januari 2011?
3. Heb je elk jaar evenveel rente in euro's gerekend? Hoe komt dat?

Op een stereo-installatie krijg je 40% korting. Je moet echter wel 19% BTW betalen. Er zijn nu twee mogelijkheden:
- De winkelier rekent eerst de prijs met koring uit en telt er vervolgens de BTW bij.
- De winkelier telt eerst de BTW bij de prijs op en trekt er dan 40% korting af.
Laat met een berekening zien wat voor jou het voordeligst is en hoeveel het scheelt.

Een leren bureaustoel van € 295,= kun je kopen voor € 200,=.
Hoeveel procent korting krijg je?

Een pak hagelslag van 250 gram kost € 1,75.
De fabrikant doet de volgende aanbieding: 20% meer voor dezelfde prijs.
Hoeveel korting krijg je dan?

Het water van de Rijn verspreidt zich als het Nederland binnenkomt over meerdere rivierarmen.

Eerst gaat 65% naar de Waal en 35% van het water naar de Nederrijn. En vervolgens splitst de Nederrijn zich vlak voor Arnhem en gaat 60% van het water naar de Lek en 40% naar de IJssel.
1. Hoeveel procent van het Rijnwater komt in het IJsselmeer terecht?
2. Hoeveel procent van het Rijnwater komt via de Lek in de Noordzee terecht?
3. In het Ruhrgebied wordt het water van de Rijn vervuild doordat er een bepaalde hoeveelheid kleurstof wordt geloosd. Onderzoekers schatten dat 640 kg van die kleurstof in de IJssel terecht is gekomen. Hoeveel kg kleurstof is er geloosd?

De tabel geeft informatie over de bevolking en de oppervlakte van het Indonesisch eilandenrijk in 1980. Er ontbreken getallen.

Bevolkingsspreiding Indonesië 1980
gebied	oppervlakte (km²)	percentage totale landoppervlakte	bevolking (mln)	percentage totale bevolking
Java/Madura	132187	6,95	91,281	61,93
Sumatra	473606	24,86	27,981	18,99
Kalimantan	539460	28,32	7,721	4,56
Sulawesi		9,93		7,04
Bali	5561	0,30	2,470	1,68
Irian Jaya	421981	22,16	1,146	0,78
Overige eilanden
		100,00		100,00

Hoeveel mensen telde Indonesië in 1980 in totaal? Geef je antwoord in miljoenen nauwkeurig.
Hoe groot was toen de oppervlakte van alle Indonesische eilanden samen?
Bereken de getallen die in de tabel ontbreken.
De bevolkingsdichtheid is het aantal mensen per km². Op welk van de met name genoemde eilanden is de bevolkingsdichtheid het grootst?
Bereken de bevolkingsdichtheid van geheel Indonesië.

Testen

Bereken:
1. 12% van 364 is ...
2. 162 is ongeveer ...% van 364
3. 364 is 54% van ...
4. 364 neemt toe tot 432, dat is een toename van ...%
5. 364 neemt met 6% toe tot ...
6. 364 neemt af met 6% tot ...
7. 364 neemt af tot 320, dat is een afname van ...%

In Nederland hebben we in 2008 zo'n 2360 km aan autosnelweg, in België is dat 1763 km. Nederland kent 56,8 km snelweg per 1000 km².
1. Hoeveel procent kilometer snelweg heeft Nederland meer dan België?
2. Hoeveel procent kilometer snelweg heeft België minder dan Nederland?
3. Hoe groot is de oppervlakte van Nederland?
4. Neem aan dat een autosnelweg gemiddeld ongeveer 20 m breed is (een rijstrook is 3,50 m breed). Hoeveel procent van Nederland is autosnelweg?
5. België heeft de grootste snelwegdichtheid van de Europese Unie. België heeft een oppervlakte van 30528 km². Hoeveel km snelweg per 1000 km² heeft België?
6. Hoeveel procent is de landoppervlakte van Nederland groter dan die van België?
7. Stel dat Nederland er in de periode 2009 - 2011 zo'n 6% km snelweg bij krijgt. Hoeveel km snelweg heeft Nederland dan in 2012?
8. Stel dat in België het aantal km snelweg in 2009 toeneemt tot 1940 km. Met hoeveel procent neemt het aantal km snelweg daar dan toe?

Je koopt een fiets met 40% korting voor € 550,00, inclusief BTW.
Hoeveel kostte die fiets zonder korting en ex.BTW?