Toepassingen
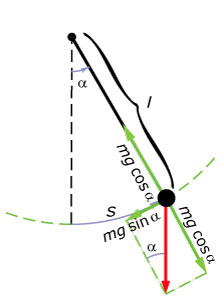
Een mathematische slinger is een (niet bestaanbare) ideale slinger. Hij is het best te benaderen door een naar verhouding kleine loden kogel aan een lange, sterke maar ragdunne draad te hangen. Als je de kogel uit zijn evenwichtsstand brengt en loslaat gaat hij slingeren. Bij de ideale slinger neem je dan aan, dat de draad geen massa heeft en geen luchtweerstand ondervindt.
De kogel wordt voortbewogen door een component van de zwaartekracht, waarvoor volgens de tweede wet van Newton geldt:
F = m · a · –mg sin(α).
- a is de versnelling (in m/s2), de afgeleide van de snelheid v (in m/s), die de afgeleide van de afgelegde weg s (in m) is;
- m is de massa in g;
- g is de zwaartekrachtversnelling;
- α is de hoek van de draad met de evenwichtsstand (in rad).