Toepassingen
Een belangrijke toepassing van de driehoek van Pascal is het binomium van Newton, een manier om (a + b)n uit te werken als n een geheel getal is. Ga na:
- (a + b)2 = (a + b)(a + b) = a2 + 2ab + b2
- (a + b)3 = (a + b)(a + b)2 = a3 + 3a2b + 3ab2 + b3
- (a + b)4 = (a + b)(a + b)3 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Leg uit, dat:
- (a + b)n = an + an – 1b1 + an – 2b2 + ... + a1bn – 1 + bn
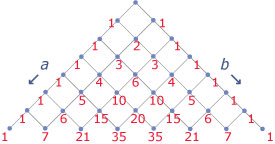 Dit is het binomium van Newton.
Dit is het binomium van Newton.Je kunt het gebruiken om uitdrukkingen als
(x + 2)8 en (y – 5)10 mee uit te werken.