Toepassingen
In een zekere stad komt een nieuwe supermarkt C naast de bestaande A en B. Deze nieuwe supermarkt zal de bestaande gaan beconcurreren. De inwoners van deze stad zullen een nieuw kooppatroon gaan ontwikkelen.
- Sommige mensen zullen (zeker als ze er vlak bij wonen) de nieuwe supermarkt gaan proberen en daar misschien wel alle boodschappen gaan doen of wellicht later naar hun oude supermarkt terugkeren.
- Sommige mensen gaan ze allemaal regelmatig bezoeken.
- Anderen blijven bij hun vertrouwde supermarkt.
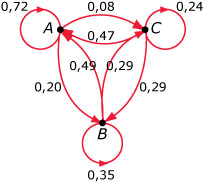Bij dit proces van wisselen van supermarkt kun je een graaf maken. De overgangskansen zijn gebaseerd op statistisch onderzoek. Zo betekent 0,72 dat 72% van de mensen die bij A winkelen dat de volgende keer ook doen. Maar 20% van de klanten van A gaan de volgende keer naar B.
Bij deze overgangsgraaf hoort een overgangsmatrix W = . Met K = geef je een klant aan die zojuist bij A winkelde.
Nu kun je door matrixvermenigvuldiging uitzoeken of zijn winkelgedrag een soort van evenwicht zal bereiken. Dit zegt dan iets over het gemiddelde winkelgedrag in deze stad op de lange duur.
