Voorbeeld

Je ziet hier een rechte kegel met top T en grondvlak een cirkel met straal MA = r. Het lijnstuk MT dat het midden van het grondvlak verbindt met de top staat loodrecht op de grondcirkel, MT = h. Voor deze kegel is r = 2 en h = 6.
Leid nu zelf een formule af voor de oppervlakte van de kegelmantel en bereken daarmee de oppervlakte van deze kegel.

Antwoord

De uitslag van zo'n kegel bestaat uit de grondcirkel en de open gevouwen kegelmantel. Deze kegelmantel is een cirkelsector met straal AT = $\sqrt{r^2+h^2}$ en middelpunt T.

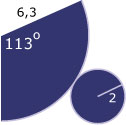De omtrek van de bijbehorende cirkel is 2π$\sqrt{r^2+h^2}$.
De omtrek van de grondcirkel van de kegel is 2πr.
De kegelmantel is daarom het $\frac{2\text{π}r}{2\text{π}\sqrt{r^2+h^2}}$ deel van een cirkel met een oppervlakte van π($\sqrt{r^2+h^2}$)².
En dus is: opp(kegelmantel) = πr$\sqrt{r^2+h^2}$.

Met r = 2 en h = 6 wordt de oppervlakte van de kegel 2π$\sqrt{40}$ + 4π.