Voorbeeld

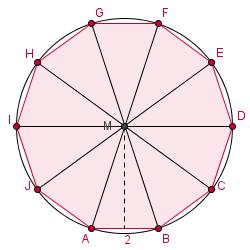
Bereken de oppervlakte van deze regelmatige tienhoek met zijden van 2 cm.

Antwoord

Van een regelmatige tienhoek zijn alle zijden en hoeken gelijk. Zo'n tienhoek past precies in een cirkel waarvan het middelpunt M in het midden van de tienhoek ligt.
De tienhoek bestaat daarom uit 10 congruente gelijkbenige driehoeken met tophoeken van 360° / 10 = 36°.

Eén van die driehoeken is ΔABM.
De hoogte h van die driehoek bereken je uit: tan(18°) = $\frac{1}{h}$.
En dus is h = $\frac{1}{\tan (18°)}$.
De oppervlakte is opp(ΔABM) = $\frac{1}{2}$ · 2 · $\frac{1}{\tan (18°)}$ = $\frac{1}{\tan (18°)}$.

De oppervlakte van de tienhoek is daarom $\frac{10}{\tan (18°)}$ ≈ 30,8 cm².