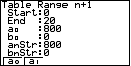Rijen met de Casio cfx-9850
Met de Casio cfx-9850 kun je op diverse manieren rijen in beeld brengen. Verder kun je daarbij ook gemakkelijk somrijen en verschilrijen maken. Je kunt tijdgrafieken en webgrafieken tekenen.
Loop eerst het practicum: 'Basistechnieken Casio cfx-9850' door.
Inhoud
Rijen met directe formules
Rijen met directe formules kunnen op drie manieren worden ingevoerd. Ga uit van de rij met voorschrift:
un = 800 · (1,05)n – 1
te beginnen met n = 1.
Je kunt de rij als een gewone functie opvatten met als domein alleen de getallen (0), 1, 2, 3, 4, ...
- Kies uit het hoofdmenu de optie TABLE
- Voer het functievoorschrift in: Y1=800*(1.05)^(X–1)
- Stel de TABLE-routine zo in: [F5] ( = Rang). Neem Start: 1; End: 10; Pitch: 1 [EXE].
- Na [F6] ( = TABLE), vind je nu de termen van de rij.
- Na [F5] ( = G CON) vind je de grafiek van deze rij, als doorgetrokken grafiek.
- Kies je [EXIT] [F6] ( = G PLT) dan krijg je een punt-grafiek.
Je kunt eenvoudig de bijbehorende verschilrij in beeld brengen via: Y2 = 800(1,05)^X en Y3 = Y2 – Y1.
Je vindt Y2 door te toetsen [VARS] en te kiezen [F4] ( = GRPH) [F1] ( = Y) 2. Voor Y1 moet je hetzelfde doen.
>>Terug
Je kunt de rij als een lijst met getallen opvatten. Je kunt hem dan invoeren in de lijsten List1, List2, enz.
Dat gaat zo:
- Kies in het hoofdmenu de optie LIST.
- Toets [EXE]. Je ziet nu een aantal lijsten List 1, List 2, enz.
- Voer in List 1 de nummers van de termen (hier bijvoorbeeld: 1, 2, 3, 4, …, 20) in door de cursor op List 1 te zetten.
Kies [OPTN] [F1] ( = LIST) [F5] ( = Seq) [X,q,T] [ , ] [X,q,T] [ , ] 1 [ , ] 20 [ , ] 1 [ ) ] [EXE].
In List 1 staan nu de getallen 1 t/m 20. Ga dat na door met de pijltjestoetsen door de lijst te lopen.
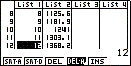
- Voer in List 2 de termen in door de cursor op List 2 te zetten.
Kies [OPTN] [F1] ( = LIST) [F5] ( = Seq) 800 [ ( ] 1,05 [ ) ] [ ^ ] [ ( ] [X,q,T] [ – ] 1 [ ) ] [ , ] [X,q,T] [ , ] 1 [ , ] 20 [ , ] 1 [ ) ] [EXE].
In List 2 komen nu de termen van de rij.
Om de bijbehorende verschilrij in beeld te krijgen moet je eerst List 3 vullen met: [OPTN] [F1] ( = LIST) [F5] ( = Seq) 800 [ ( ] 1,05 [ ) ] [ ^ ] [X,q,T] [ , ] [X,q,T] [ , ] 1 [ , ] 20 [ , ] 1 [ ) ] [EXE].
De bijbehorende verschilrij kun je nu in List 4 in beeld krijgen door de cursor op List 4 te zetten en dan te toetsen: [OPTN] [F1] ( = LIST) [F1] ( = List) 3 [ – ] [F1] ( = LIST) 2 [EXE].
De bijbehorende somrij kan nu in List 5 als volgt ingevoerd worden.
Zet de cursor op List 5. Toets dan: [OPTN] [F1] ( = LIST) [F6] ( –> ) [F6] ( –> ) [F3] ( = Cuml) [F6] ( –> ) [F1] ( = LIST) 2 [EXE].
>>Terug
Je kunt tenslotte de rij invoeren via RECUR uit het hoofdmenu.
Nadat je RECUR geopend hebt toets je [F3] ( = TYPE). Je kiest dan [F1] ( = an). De keuzebalk verschijnt op (an:) in het Recursion-scherm.
Vul achter an de formule: 800(1,05)^(n - 1) in gevolgd door [EXE].
De n vind je bij [F4] ( = n).
Toets nu [F5] ( = RANG). Je krijgt nu het scherm: (Table Range n). Toets achter Start: 1 [EXE] en achter End: 20 [EXE]. Na [F6] ( = TABL) krijg je een lijst van de rij.
Door gebruik te maken van [F5] ( = G-CON) krijg je een doorgetrokken grafiek van deze rij.
Toets je [F6] ( = G-PLT) dan krijg je een puntgrafiek van de rij. Je moet wel het (V-Window) aanpassen.
Toets [SHIFT] [MENU] ( = SET UP). Zet (? Display) op (On) door [F1] [EXE] te toetsen.
Vraag je de rekenmachine een tabel te maken: [F6] ( = TABLE) dan krijg je in een tabel naast de rij ook de somrij. Loop met de pijltjestoetsen door de lijsten.
Bij (G-CON) en (G-PLT) moet je nu een keuze maken van welke rij je een grafiek wil zien.
Maak een grafiek van de rij waarbij n loopt van 1 t/m 20.
Oefen het werken met rijen gegeven door een directe formule.
>>Terug
Rijen met recursieve formules
Als je een rij die gegeven is door een recursieve formule wilt invoeren, moet je in het hoofdmenu van de Casio kiezen voor RECUR.
Bekijk nog eens de rij met direct voorschrift:
un = 800 · (1,05)n – 1
te beginnen met n = 1.
In recursieve vorm ziet diezelfde rij er zo uit:

 In het RECUR-menu is de rij ook als recursieve formule in te voeren.
In het RECUR-menu is de rij ook als recursieve formule in te voeren.
Bij de Casio kies je dan [F3] ( = TYPE) en kiest [F2] ( = an + 1).
Achter (an + 1:) toets je dan 1,05an. De factor (an) vind je door [F4] ( = n.an) [F2] ( = an) [EXE].
Als je [F5] ( = RANG) toetst krijg je het (Table Range n + 1) -scherm.
Vul dit scherm als volgt in: Start: 0 [EXE]; End: 20 [EXE]; [F1] ( = a0) geeft a0: 800 [EXE] [EXE].
Toets nu [F6] ( = TABL).
Maak een grafiek van de rij waarbij n loopt van 1 t/m 20.
Oefen het werken met rijen gegeven door een recursieve formule.
>>Terug
Tijdgrafiek en webgrafiek
Je kunt bij rijen twee soorten grafieken maken:
- 'gewone' grafieken of tijdgrafieken
- webgrafieken
 Na uit het hoofdmenu RECUR te hebben gekozen en een tabel: [F6] ( = TABL) van de rij gemaakt te hebben kun je met [F4] ( = WEB) en [F5] ( = G-CON) deze grafieken laten tekenen.
Na uit het hoofdmenu RECUR te hebben gekozen en een tabel: [F6] ( = TABL) van de rij gemaakt te hebben kun je met [F4] ( = WEB) en [F5] ( = G-CON) deze grafieken laten tekenen.
Gebruik weer dezelfde rij als in de rest van het practicum met directe formule:
un = 800 · (1,05)n – 1
en recursieve formule:

De tijdgrafiek verschijnt netjes in beeld als de formule is ingevoerd en de juiste scherminstellingen (n loopt van 1 t/m 20 en u(n) loopt van ongeveer 800 tot 2000) en tabelinstellingen zijn gekozen. Bij de rij in dit practicum moet je voor de volgende instellingen zorgen.
Eerst zorg je voor de instellingen van het (View Window):
[SHIFT] [F3] ( = V-Window) 0 [EXE] 20 [EXE] 1 [EXE] 800 [EXE] 2000 [EXE] 1 [EXE].
Daarna zorg je voor de instellingen van het (Table Range n+ 1)-scherm:
[F5] ( = RANG) 0 [EXE] 20 [EXE] 800 [EXE] pijltjestoets omlaag en 800 [EXE] en pijltjestoets omlaag en [EXE].
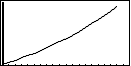
Toets nu: [F6] ( = TABL) [F5] ( = G-CON). Je krijgt nu een continue tijdgrafiek van de rij.
Toets je nu: [EXIT] [F6] ( = G-PLT), dan krijg je een puntgrafiek van de rij.
Om de webgrafiek in beeld te krijgen moet je (V-Window)-scherm aanpassen.
Pas het venster zo aan, dat zowel in de x-richting als in de y-richting de rijtermen (lopend van 800 naar 1200 en nog groter) op het scherm passen. Bijvoorbeeld:
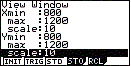
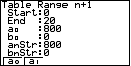
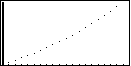
Toets nu: [F6] ( = TABL) [F4] ( = WEB) Je ziet twee lijnen in beeld komen.
Eén daarvan is de lijn y = x.
De ander wordt bepaald door de rij (de bijbehorende theorie vind je in het informatieboek).

Werk nu met [EXE] en de pijltjestoetsen.
Je vindt telkens twee opeenvolgende termen van de rij, te weten x = u(n – 1) en y = u(n).
In de grafiek zie je de cursor springen van de lijn y = x naar de lijn die door de rij wordt bepaald en weer terug, en zo maar steeds door.

>>Terug


 In het RECUR-menu is de rij ook als recursieve formule in te voeren.
In het RECUR-menu is de rij ook als recursieve formule in te voeren. Na uit het hoofdmenu RECUR te hebben gekozen en een tabel: [F6] ( = TABL) van de rij gemaakt te hebben kun je met [F4] ( = WEB) en [F5] ( = G-CON) deze grafieken laten tekenen.
Na uit het hoofdmenu RECUR te hebben gekozen en een tabel: [F6] ( = TABL) van de rij gemaakt te hebben kun je met [F4] ( = WEB) en [F5] ( = G-CON) deze grafieken laten tekenen.