Kansverdelingen met de Casio cfx-9850
Met de Casio cfx-9850 kun je in verschillende standaardsituaties kansen berekenen. In dit practicum komen de normale kansverdeling en de binomiale kansverdeling aan bod. Je moet voordat je met dit practicum kunt werken bekend zijn met de basistechnieken van de Casio cfx-9850 en het werken met functies op de Casio cfx-9850. Doe eventueel eerst de bijbehorende practica.
Loop ook eerst het practicum: 'Simulaties en telsystemen met de Casio cfx-9850' door.
Inhoud
De normale kansverdeling
Je vindt op de Casio cfx-9850 kansverdelingen als je in het hoofdmenu kiest voor STAT.
Als een toevalsvariabele X normaal is verdeeld met een gemiddelde van 100 en een standaardafwijking van 6, dan kun je de volgende kansen berekenen:
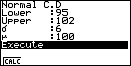
-
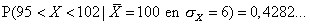
- je kiest: [ F5 ] ( = DIST) [ F1 ] ( = NORM) [ F2 ] ( = Ncd) om het (Normal C.D)-scherm te krijgen
- toets nu : 95 [EXE] 102 [EXE] 6 [EXE] 100 [EXE] [ F1 ] ( = CALC).
-

- met [EXIT] kom je terug in het (Normal C.D)-scherm; anders zoek je dat scherm weer vanaf het hoofdmenu op
- toets nu: [ (–) ] 1 [EXP] 99 [EXE] 95 [EXE] 6 [EXE] 100 [EXE] [ F1 ] ( = CALC).
-

- zoek eerst het (Normal C.D)-scherm op
- toets nu: 95 [EXE] 1 [EXP] 99 [EXE] 6 [EXE] 100 [EXE] [ F1 ] ( = CALC).
Loop al deze berekeningen zelf na!
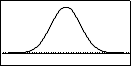 Je kunt ook de normale verdeling met gemiddelde 100 en standaardafwijking 6 in beeld brengen.
Je kunt ook de normale verdeling met gemiddelde 100 en standaardafwijking 6 in beeld brengen.
Kies uit het hoofdmenu: STAT. Door te toetsen: [F5] ( = DIST) [F1] ( = NORM) [F1] ( = Npd) kom je bij het (Normal P.D)-scherm.
Vul dit als volgt in: [ V ] 6 [EXE] 100 [EXE].
Toets nu [F6] ( = DRAW) en je ziet de grafiek die bij de normaalverdeling hoort.
Het weergeven van kansen als oppervlakte onder de normale verdeling kan met de Casio cfx-9850 echter alleen door over te stappen op de standaardnormale verdeling. Je moet de gewenste kans dus eerst omrekenen naar een kans bij de standaardnormale verdeling.
Daarbij kun je het bijpassende gebied onder de standaardnormaalkromme laten aangeven.
 Die standaardnormaalkromme vind je door in het hoofdmenu te kiezen voor RUN.
Die standaardnormaalkromme vind je door in het hoofdmenu te kiezen voor RUN.
Met [SHIFT] [ F4 ] ( = Sketch) [ F1 ] ( = Cls) [EXE] laat je eventueel aanwezige grafieken verdwijnen.
Toets nu: [ F5 ] ( = GRPH) [ F1 ] ( = Y=) [OPTN] [ F6 ] ( = > ) [ F3 ] ( = PROB) [ F6 ] ( = >).
Er zijn nu een aantal mogelijkheden:
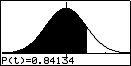
- door in te toetsen [ F1 ] ( = P( ) 1 [ ) ] [EXE] zie je de standaardnormaalkromme met het gebied gearceerd dat de kans op z < 1 aangeeft (je neemt in de praktijk in plaats van 1 de z-waarde die bij de gevraagde kans hoort)
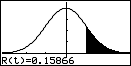
- door in te toetsen [ F3 ] ( = R( ) 1 [ ) ] [EXE] zie je de standaardnormaalkromme met het gebied gearceerd dat de kans op z > 1 aangeeft (je neemt in de praktijk in plaats van 1 de z-waarde die bij de gevraagde kans hoort)
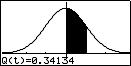
- door in te toetsen [ F2 ] ( = Q( ) 1 [ ) ] [EXE] zie je de standaardnormaalkromme met het gebied gearceerd dat de kans op 0 < z < 1 aangeeft (je neemt in de praktijk in plaats van 1 de z-waarde die bij de gevraagde kans hoort)
Met de [AC/ON]-toets verlaat je telkens het venster.
>>Terug
Grenswaarden bij normale kansverdelingen
Terugrekenen vanuit gegeven kansen bij de normale verdeling kan ook gemakkelijk met de Casio cfx-9850.
Je wilt dan bij een normaal verdeelde variabele X bij een gegeven kans de bijbehorende grenswaarde g voor X terugzoeken:
-
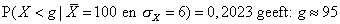
- Kies uit het hoofdmenu: STAT.
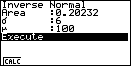
Je toetst dan: [ F5 ] ( = DIST) [ F1 ] ( = NORM) [ F3 ] ( = InvN) om het (Inverse Normal)-scherm te krijgen.
- Toets 0.2023 [ EXE ] 6 [ EXE ] 100 [ EXE ] en daarna [ F1 ] ( = CALC ) en je vindt de grenswaarde.
-
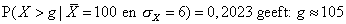
Omdat P(X > g) = 1 – P(X < g), is nu: P(X < g) = 1 – 0,2023 = 0,7977. Daarom:
- Ga naar het (Inverse Normal)-scherm.
- Toets 0.7977 [ EXE ] 6 [ EXE ] 100 [ EXE ] en je vindt de grenswaarde.
Loop ook deze berekeningen zorgvuldig na!
>>Terug
De binomiale kansverdeling
Als een variabele X binomiaal is verdeeld met n = 60 en p = 0,42 dan kun je de volgende binomiale kansen berekenen met de Casio cfx-9850:
- P(X = 26 | n = 60 en p = 0,42) = 0,10125...
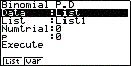
- Ga naar het STAT-menu. Je toetst: [ F5 ] ( = DIST) [ F5 ] ( = BINM) [ F1 ] ( = Bpd). Je krijgt dan dit scherm in beeld.
- De keuzebalk staat op Data. Kies: [F2] ( = Var) en ga met de pijltjestoets naar beneden.
- Vul bij x het getal 26, bij Numtrial 60 en bij p het getal 0.42 in en ga naar Execute en [ EXE ].
- P(X < 26 | n = 60 en p = 0,42) = 0,63526...
- Ga naar het STAT-menu. Je toetst: [ F5 ] ( = DIST) [ F5 ] ( = BINM) [ F2 ] ( = Bcd).
- De keuzebalk staat op Data. Kies: [F2] ( = Var) en ga met de pijltjestoets naar beneden.
- Vul bij x het getal 26, bij Numtrial 60 en bij p het getal 0.42 in en ga naar Execute en [ EXE ].
- P(X < 26 | n = 60 en p = 0,42) = P(X < 25 | n = 60 en p = 0,42) = 0,534...
- Ga naar het STAT-menu. Je toetst: [ F5 ] ( = DIST) [ F5 ] ( = BINM) [ F2 ] ( = Bcd).
- De keuzebalk staat op Data. Kies: [F2] ( = Var) en ga met de pijltjestoets naar beneden.
- Vul bij x het getal 25, bij Numtrial 60 en bij p het getal 0.42 in en ga naar Execute en [ EXE ].
- P(X > 26 | n = 60 en p = 0,42) =
1 – P(X < 26 | n = 60 en p = 0,42) = 1 – 0,63526... = 0,36474...
- Als bij de tweede van boven.
- P(X > 26 | n = 60 en p = 0,42) = 1 – P(X < 25 | n = 60 en p = 0,42) = 1 – 0,534... = 0,466...
- Als bij de derde van boven.
>>Terug
Kanshistogrammen bij de binomiale verdeling
Bij een binomiale kansverdeling kun je een kanshistogram maken.
Je laat dan de grafische rekenmachine een lijst met kansen maken. Stel bijvoorbeeld dat je een kanshistogram wilt maken bij een binomiale verdeling met n = 20 en p = 0,4.
Dat kun je zo doen:
- Kies het STAT-menu. Je krijgt dan een schem met een aantal lijsten: List 1, List 2, enzovoorts.
Als er in en van de lijsten nog gegevens staan, ga dan met de keuzebalk boven die lijst staan.
Kies de optie DEL-A door te toetsen: [ F6 ] [ F4 ] ( = DEL-A). Bevestig met [F1] ( = YES).
De betreffende lijst is nu leeg. Doe dat met alle lijsten waar nog wat in staat.
- Voer in List 1 de waarden voor de stochast X = 0, 1, 2, …, 20 in door de keuzebalk op List 1 te zetten.
Kies: [OPTN] gevolgt door [F1] ( = List) [F5] ( = Seq).
Je ziet nu onder in het scherm: Seq (met daar achter een knipperende cursor).
Toets: [X,q,T] [ , ] [X,q,T] [ , ] 0 [ , ] 20 [ , ] 1 [ ) ].
In het scherm staat nu: Seq( X, X , 0, 20, 1).
Toets je nu [EXE] dan is de lijst List 1 gevuld met de getallen 0, 1, 2,....., 20.
- Vul nu lijst List 2 met de binomiale kansen door de keuzebalk op List 2 te zetten en: [OPTN] [ F1 ] ( = List) [F5] ( = Seq).
Vul nu aan tot Seq(20CX*(0,4)^X*(0,6)^(20 – X), X, 0, 20,1) door te toetsen:
20 [OPTN] [ F3 ] ( = PROB) [ F3 ] ( = nCr) [X,q,T] [ x ] [ ( ] 0.4 [ ) ] [ ^ ] [X,q,T] [x] [ ( ] 0.6 [ ) ] [ ^] [ ( ] 20 [ x ] [X,q,T] [ ) ] [ , ] [X,q,T] [ , ] 0 [ , ] 20 [ , ] 1 [ ) ].
Toets [EXE] en lijst 2 is gevuld met de bijbehorende kansen. Controleer dat.

- Nu je de lijsten L1 en L2 hebt ingevoerd, kun je diagrammen maken.
Toets zo vaak op [EXIT] als nodig om onder in het scherm GRPH bij [ F1 ] en CALC bij [ F2 ] te krijgen.
Toets [ F1 ] ( = GRPH) en kies [ F6 ] ( = SET). Je krijgt nu het StatGraph1-scherm.
Laat de eerste regel op StatGraph1 staan.
Ga met de pijltjestoets naar Graph Type en kies voor de optie [ F6 ] [ F1 ] ( = Hist).
Kies bij XList: [ F1 ] ( = List1).
Kies bij Frequentie: [ F3 ] ( = List2) en [EXE].
 Toets nu op [ F1 ] = (GPH1).
Toets nu op [ F1 ] = (GPH1).
Je krijgt dan het Set Interval scherm.
Toets je [ F6 ] ( = DRAW) dan zie je dat de machine een verdeling van 10 even grote klassen met een breedte van 2,23 tekent. Mooier zou zijn als er 21 klassen met een breedte van 1 getekend zou worden. Toets [EXIT] [ F1 ] ( = GPH1). Verander Pitch: 2,23 in Pitch: 1 [EXE] [F6] ( = DRAW).
Oefen jezelf door zo een paar kanshistogrammen bij de binomiale verdeling te maken. Cumulatieve kanshistogrammen lukken ook.
>>Terug

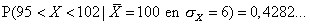


 Je kunt ook de normale verdeling met gemiddelde 100 en standaardafwijking 6 in beeld brengen.
Je kunt ook de normale verdeling met gemiddelde 100 en standaardafwijking 6 in beeld brengen. Die standaardnormaalkromme vind je door in het hoofdmenu te kiezen voor RUN.
Die standaardnormaalkromme vind je door in het hoofdmenu te kiezen voor RUN.


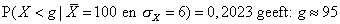
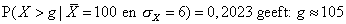


 Toets nu op [ F1 ] = (GPH1).
Toets nu op [ F1 ] = (GPH1).