Negatieve getallen aftrekken

Verkennen

Opgaven

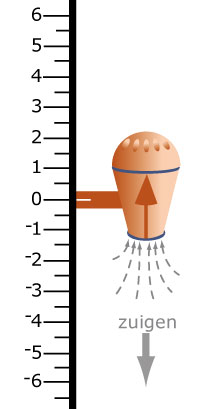
1. Je ziet hiernaast een tekening van het zuig/blaas-motortje.
   Dit motortje kan bewegen langs een verticale as. In de stand "blazen" gaat hij in de richting van de pijl, in de stand "zuigen" gaat hij tegen de richting van de pijl in. Verder kent de motor twee standen, omhoog en omlaag. Dat zie je aan de pijl.
   1. Het motortje start op 0 en kan alleen zuigen. Je stelt in "3 omhoog". Waar eindigt het motortje?
   2. Het motortje start op 0 en kan alleen zuigen. Je stelt in "3 omlaag". Waar eindigt het motortje?
   3. Je start nu op 3 en stelt in "2 omhoog". Waar eindigt het motortje? Welke aftrekking hoort daar bij?
   4. Je start weer op 3 en stelt in "5 omlaag". Waar eindigt het motortje? Welke aftrekking hoort daar bij?


2. Hopelijk heb je nu gezien dat bij het zuig/blaas-motortje het zuigen betekent dat er getallen worden afgetrokken. De stand van het motortje is "omhoog" (voor positieve getallen) en "omlaag" voor negatieve getallen.
   1. Hoe laat je het motortje de aftrekking `3 - 4` maken?
   2. Hoe laat je hem de aftrekking ^–`3 - 4` maken?
   3. Hoe laat je hem de aftrekking 3 – ^–4 maken?
   4. Hoe laat je hem de aftrekking ^–3 – ^–4 maken?


3. Je hebt nu steeds het motortje alleen laten blazen (optellingen) of alleen laten zuigen (aftrekkingen). Maar je kunt die twee acties ook door elkaar gebruiken.
   1. Leg uit met behulp van de standen en de acties van het motortje dat 5 + ^–2 hetzelfde effect heeft als `5 - 2`.
   2. Verklaar zo ook dat 5 – ^–2 = 5 + 2.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Negatieve getallen aftrekken > Uitleg

In de Uitleg kun je nalezen hoe je getallen kunt voorstellen als pijlen op de getallenlijn. Meestal teken je zo'n lijn niet van boven naar beneden, maar van links naar rechts. Omhoog is dan naar rechts (en geeft een positief getal aan, blauwe pijl), omlaag is naar links (en geeft een negatief getal aan, rode pijl). Aftrekken betekent pijlen achter elkaar leggen, maar nu komt de kop van de tweede pijl aan de punt van de eerste pijl te zitten want je moet als het ware "terug bewegen".

Opgaven

4. Hier zie je vier aftrekkingen. Teken ze op de getallenlijn en schrijf de uitkomst op. Je ziet nu mintekens die een verschillende betekenis hebben. Let goed op of het een negatiefteken is of de bewerking "aftrekken" voorstelt.
   1. `3 - 4`
   2. `3 - -4`
   3. `-3 - 4`
   4. `-3 - -4`


5. Bereken (zonder rekenmachine):
   1. `-12 - -33`
   2. `15 - -26`
   3. `-1 - 5 - -9`
   4. `365 - -215`


6. Verbeter de fouten in deze berekeningen:
   1. `-12 - 15 = -3`
   2. `-3 - -12 = -15`
   3. `8 - (-6 - 12) = -10`
   4. `13 - -14 = 1`


7. Bekijk de Uitleg, pagina 2. Je ziet hoe je in een berekening het aantal tekens kunt verminderen. Pas dit in de volgende berekeningen toe en bereken (zonder rekenmachine) het eindantwoord.
   1. `5 - -7`
   2. `-5 + -7`
   3. `-5 - -7 + -2`
   4. `35 - -40 - - 12`

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Negatieve getallen aftrekken > Voorbeeld 1

In Voorbeeld 1 zie je nog enkele aftrekkingen uitgebeeld met de getallenlijn. Je kunt dit oefenen met de Min-applet.

Opgaven

8. Maak eerst de eerste drie aftrekkingen uit Voorbeeld 1 met de applet.
   Oefen vervolgens met een medeleerling. Geef elkaar een optelling op en bepaal het antwoord. Controleer dit antwoord met de Min-applet.
   


9. Bereken (bekijk eventueel eerst de vierde berekening in het voorbeeld):
   1. `-35 - 16`
   2. `-12 - -16 - 28`
   3. `19 - -41 - 21`
   4. `-12 - 16 - -14`


10. Er is nog een tweede min-applet: Min-applet-2.
    Je ziet daarin een andere manier om naar een aftrekking van twee getallen te kijken.
    1. Bepaal met deze applet `-4 - 6` en leg het antwoord uit.
    2. Bepaal met deze applet `-2 - -4` en leg het antwoord uit.
    3. Bepaal met deze applet `2 - -5` en leg het antwoord uit.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Negatieve getallen aftrekken > Voorbeeld 2

Soms zijn de getallen nogal vervelend en kun je beter een rekenmachine gebruiken. Vooraf je antwoord schatten is dan toch nog steeds nuttig.

Opgaven

11. Schat bij de volgende aftrekkingen eerst het antwoord en bereken het dan met de rekenmachine. Denk om het gebruik van het juiste negatiefteken!
    1. `-12,64 - -33,83`
    2. `143,4 - -86,12`
    3. `239 - (-132 + 67)`
    4. `-0,012 - -1,265`


12. Vul de open plaatsen in.
    1. `6,3 - ... = -2`
    2. `... - -4,4 = 8,3`
    3. `... - -2,5 = -6,1`
    4. `8,16 - ... = 0`

Oefenen

13. Breng met behulp van pijlen op de getallenlijn de volgende berekeningen in beeld en schrijf het antwoord op:
    1. `5 - -2`
    2. `-3 - -8`
    3. `-4,3 + -7`
    4. `6,4 + -2,05`
    5. `-2,15 + -3,31`
    6. `0,5 + 4,3 - 2,1`
    7. `-1,7 - -2,4 - 3,1`
    8. `-15 - (12 - -3)`


14. Vul de lege plaatsen in.
    1. `8 - ... = -4`
    2. `-5 - ... = -19`
    3. `7,03 - -21,18 = ...`
    4. `... - -34 = -12`
    5. `... - -12 = 10`
    6. `24 - ... = -1`
    7. `13 - ... = -5`
    8. `15,4 - -0,7 = ...`


15. Het water in de IJssel bij Zutphen staat 2,43 m boven NAP. Normaal staat het water daar 0,95 m onder NAP. Drie leerlingen berekenen het verschil in hoogte:
    • Jasper: 0,95 m onder NAP is -0,95. Dus: `-0,95 + 2,43 = 1,48` m.
    • Selma: Je moet doen: `2,43 - -0,95 = 3,38` m.
    • Jörg: `-0,95 - 2,43 = -3,38` m.
    1. Wie heeft er gelijk? Leg ook uit waarom.
    2. Hoeveel bedraagt het verschil in hoogte tussen 3,57 m boven NAP en 2,71 m onder NAP?


16. Je ziet hier een kruisgetallenpuzzel. Vul de puzzel in, een negatiefteken komt in het vakje van het eerste cijfer van een getal.
    
    
    
    

    Horizontaal		Verticaal
    1	`8 - -4`	1	`170 - 1`
    2	`15 - -37`	2	`15 - -37`
    3	`11 - 89`	4	`83 - -100 - -95`
    5	`150 - -50 + -9`	5	`118 - -5`
    7	`-12 - 5`	6	`-99 + 207`
    8	`55 - -5 - 5`	10	`-(20 - 2)`
    9	`278 - -40`	11	`-15 + 35`
    10	`-20 - -6`
    11	`-47 - -336`
    12	`-4 - 8`
    13	`27 - -26`

    
    


17. Een kompas op een schip geeft nooit helemaal de juiste richting aan. Dat komt door de "variatie" (de plaatselijke afwijking) en de "deviatie". De deviatie is de afwijking in koers die door het schip veroorzaakt wordt. Als je de werkelijke koers weet en de variatie, dan kun je de deviatie uitrekenen:

    deviatie = werkelijke koers – kompaskoers – variatie

    Je werkelijke koers is bijvoorbeeld 81°, de variatie is `-5`° en op je kompas lees je af: 77°.
    Je deviatie is dan: deviatie `= 81 - 77 - -5`.
    1. Wat is de uitkomst van de bovenstaande berekening?
    2. Voor een ander schip geldt een andere deviatie. Veronderstel dat de werkelijke koers van een schip 125° is. De variatie is `-3`° en de kompaskoers 129°. Wat is de deviatie van dat schip?

Toepassen

18. Temperatuursverschillen

    Deze tabel geeft de temperatuur op een winterdag.
    
    

    tijdstip (uur)	0	2	4	6	8	10	12	14	16	18	20	22	24
    temperatuur (°C)	–5	–6	–8	–9	–7	–4	–1	2	3	2	–1	–4	–5

    
    
    1. Hoeveel bedraagt het verschil tussen de hoogste en de laagste temperatuur die dag?
    2. Maak een tabel waarin je op elk tijdstip dat in de gegeven tabel voorkomt het temperatuursverschil met de voorgaande meting aangeeft.
    3. Tussen welke tijdstippen is de temperatuur het snelst gestegen? En op tussen welke tijdstippen is de temperatuur het snelst gedaald?



19. Negatieve breuken 2

    Je kunt ook met negatieve breuken aftrekkingen uitvoeren. Doe ze zonder rekenmachine.
    1. `1/3 - -1/2`
    2. `1 5/6 - 2 1/3`
    3. `-3/4 - 1 1/8`
    4. `2 1/4 - -3 2/7`