Negatieve getallen optellen

Verkennen

Opgaven

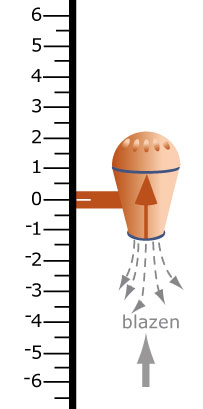
1. Je ziet hiernaast een tekening van het zuig/blaas-motortje.
   Dit motortje kan bewegen langs een verticale as. In de stand "blazen" gaat hij in de richting van de pijl, in de stand "zuigen" gaat hij tegen de richting van de pijl in. Verder kent de motor twee standen, omhoog en omlaag. Dat zie je aan de pijl.
   1. Het motortje start op 0 en kan alleen blazen. Je stelt in "3 omhoog". Waar eindigt het motortje?
   2. Het motortje start op 0 en kan alleen blazen. Je stelt in "3 omlaag". Waar eindigt het motortje?
   3. Je start nu op 3 en stelt in "2 omhoog". Waar eindigt het motortje? Welke optelling hoort daar bij?
   4. Je start weer op 3 en stelt in "5 omlaag". Waar eindigt het motortje? Welke optelling hoort daar bij?


2. Hopelijk heb je nu gezien dat bij het zuig/blaas-motortje het blazen betekent dat er getallen worden opgeteld. De stand van het motortje is "omhoog" (voor positieve getallen) en "omlaag" voor negatieve getallen.
   1. Hoe laat je het motortje de optelling `3 + 4` maken?
   2. Hoe laat je hem de optelling ^–3 + 4 maken?
   3. Hoe laat je hem de optelling 3 + ^–4 maken?
   4. Hoe laat je hem de optelling ^–3 + ^–4 maken?

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Negatieve getallen optellen > Uitleg

In de Uitleg kun je nalezen hoe je getallen kunt voorstellen als pijlen op de getallenlijn. Meestal teken je zo'n lijn niet van boven naar beneden, maar van links naar rechts. Omhoog is dan naar rechts (en geeft een positief getal aan, blauwe pijl), omlaag is naar links (en geeft een negatief getal aan, rode pijl). Optellen betekent pijlen achter elkaar leggen: de staart van de tweede pijl komt dan aan de punt van de eerste pijl te zitten.

Opgaven

3. Hier zie je vier optellingen. Teken ze op de getallenlijn en schrijf de uitkomst op. Met het minteken wordt steeds het negatiefteken bedoeld, want in dit onderdeel gaat het alleen over optellingen.
   1. `3 + 4`
   2. `3 + -4`
   3. `-3 + 4`
   4. `-3 + -4`


4. Bereken:
   1. `-12 + -33`
   2. `15 + -26`
   3. `-1 + 5 + -9`
   4. `365 + -215`


5. Verbeter de fouten in deze berekeningen:
   1. `-12 + 15 = -27`
   2. `-3 + -12 = -9`
   3. `8 + (-6 + 12) = -10`
   4. `13 + -14 = 1`

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Negatieve getallen optellen > Voorbeeld 1

In Voorbeeld 1 zie je nog enkele optellingen uitgebeeld met de getallenlijn. Je kunt dit oefenen met de Plus-applet.

Opgaven

6. Maak eerst de eerste drie optellingen uit Voorbeeld 1 met de applet.
   Oefen vervolgens met een medeleerling. Geef elkaar een optelling op en bepaal het antwoord. Controleer dit antwoord met de Plus-applet.
   


7. Bereken (bekijk eventueel eerst de vierde berekening in het voorbeeld):
   1. `-35 + 16`
   2. `-12 + -16 + 28`
   3. `19 + -41 + 21`
   4. `-12 + 16 + -14`

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Negatieve getallen optellen > Voorbeeld 2

Soms zijn de getallen nogal vervelend en kun je beter een rekenmachine gebruiken. Vooraf je antwoord schatten is dan toch nog steeds nuttig.

Opgaven

8. Schat bij de volgende optellingen eerst het antwoord en bereken het dan met de rekenmachine. Denk om het gebruik van het juiste negatiefteken!
   1. `-12,64 + -33,83`
   2. `143,4 + -86,12`
   3. `239 + (-132 + 67)`
   4. `-0,012 + -1,265`


9. Vul de open plaatsen in.
   1. `6,3 + ... = -2`
   2. `... + -4,4 = 8,3`
   3. `... + -2,5 = -6,1`
   4. `8,16 + ... = 0`

Oefenen

10. Breng met behulp van pijlen op de getallenlijn de volgende optellingen in beeld en schrijf het antwoord op:
    1. `5 + -2`
    2. `-3 + -8`
    3. `-4,3 + 7`
    4. `-6,4 + -2,05`


11. Vul de lege plaatsen in.
    1. `8 + ... = -4`
    2. `-5 + ... = -19`
    3. `7,03 + -21,18 = ...`
    4. `... + -34 = -12`
    5. `... + -12 = 10`
    6. `24 + ... = -1`
    7. `13 + ... = -5`
    8. `15,4 + -0,7 = ...`


12. De scheikundige Ron Onderwater werkt veel met vloeistoffen. Hij heeft een vloeistof van 5°C en voegt daar een vloeistof aan toe die de temperatuur 8 graden doet afnemen.
    1. Wat wordt de temperatuur van de nieuwe vloeistof?
    2. De berekening die erbij hoort staat hier gedeeltelijk. Maak de hem af (er staat een + omdat de vloeistof erbij wordt gedaan).
       `5 + ... = ...`
    3. Vervolgens voegt hij een vloeistof toe die de temperatuur 12 graden doet afnemen. Welke temperatuur heeft het mengsel nu? Schrijf een bijpassende berekening op als hierboven.
    4. De scheikundige schrijft op: `-15 + -10 = ...`
       Maak de berekening af en vertel wat hij heeft gedaan.


13. Als je werkt met een kompas is je werkelijke koers altijd anders dan je kompas aangeeft. Dat komt omdat de magnetische noordpool niet samenvalt met de werkelijke noordpool. Op iedere plaats op aarde is een correctie nodig. Dat heet de "variatie". Die moet je optellen bij de koers die je kompas aangeeft.
    Je bent bijvoorbeeld ergens waar de variatie `-3` is en je kompas wijst 294° aan. Je werkelijke koers is dan: `294 + -3 = 291`°.
    1. Je kompas wijst 21° aan. Wat is je werkelijke koers als de variatie `-9` is? Schrijf ook een berekening op.
    2. Je werkelijke koers is 187° en je kompas wijst 201° aan. Hoeveel is de variatie op de plaats waar je je bevindt?
    3. Hoeveel is de variatie wanneer je kompas exact de juiste richting aanwijst?
    4. Je wil een koers van 108 aanhouden waar de variatie `-7` is. Welke richting moet je op je kompas aanhouden?


14. Hendrik heeft een schuld van € 1250 bij de bank. Toch neemt hij nog eens € 450 van zijn rekening op.
    1. Hoe hoog is dan zijn schuld?
    2. Schrijf een bijpassende berekening op. Gebruik daarin negatieve getallen voor schuld.
    3. Een maand later krijgt hij € 1850 loon. Maar hij geeft meteen € 2100 uit. Bereken zijn nieuwe banksaldo.


15. Neem een stuk roosterpapier en teken daarop een assenstelsel. Je gaat in dit assenstelsel routes lopen en moet bedenken waar je na tien stappen bent gekomen. Elke stap wordt beschreven door de uitdrukking: `...` horizontaal en ... verticaal.
    Met "horizontaal" wordt evenwijdig aan de `x`-as bedoeld en met "verticaal" evenwijdig aan de `y`-as. Je begint steeds in `(0,0)`.
    1. In welk punt ben je aangekomen als je tien keer de stap `2` horizontaal en `-1` verticaal hebt gezet?
    2. Je zet eerst de stap `2` horizontaal en `-1` verticaal en dan de stap `-1` horizontaal en `-2` verticaal en dit herhaal je vijf keer. In welk punt ben je dan?
    3. Je begint met de stap `1` horizontaal en `1` verticaal. Elke volgende stap ga je horizontaal 1 eenheid meer en verticaal 1 eenheid minder. Waar ben je na in totaal tien stappen?

Toepassen

16. Gemiddelde dagtemperatuur

    Deze tabel geeft de temperatuur op een winterdag.
    
    

    tijdstip (uur)	0	2	4	6	8	10	12	14	16	18	20	22	24
    temperatuur (°C)	–5	–6	–8	–9	–7	–4	–1	2	3	2	–1	–4	–5

    
    
    1. Bereken de gemiddelde temperatuur van die dag.
    2. Bereken ook de gemiddelde temperatuur overdag (vanaf 8:00 uur tot 20:00 uur) en de gemiddelde temperatuur 's nachts.
    3. Hoeveel verschilt de gemiddelde nachttemperatuur van de gemiddelde temperatuur overdag?



17. Negatieve breuken 1

    Je kunt op de getallenlijn ook met breuken werken. Uiteraard bestaan er ook "negatieve breuken": breuken met een negatiefteken. Je kunt immers ook delen van eenheden naar links op de getallenlijn uitzetten.
    1. Teken een getallenlijn waarom je twaalfden kunt aangeven. Laat hem van `-2` tot 2 lopen, dus van `-24/12` tot `24/12`.
    2. Geef daarop de optelling `-5/12 + 11/12` aan.
    3. Teken ook `-5/12 + -11/12`.
    4. En tenslotte nog `1/6 + -5/12`.
    Je kunt nu ook met negatieve breuken optellingen uitvoeren. Doe ze zonder rekenmachine.
    5. `1/3 + -1/2`
    6. `-1 5/6 + -2 1/3`
    7. `-3/4 + 1 1/8`
    8. `-2 1/4 + -3 2/7`