Wat is negatief?

Verkennen

Opgaven

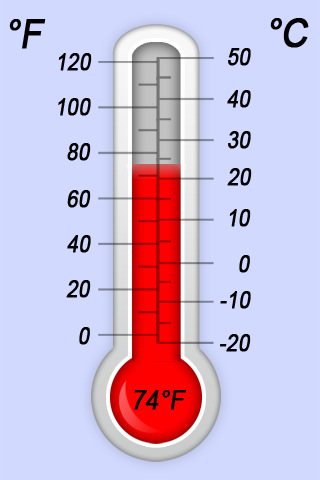
  1. Op de Iphone is deze thermometer als app beschikbaar. De temperatuur staat er niet alleen in graden Celsius, maar ook in graden Fahrenheit. Dat komt omdat in veel Engelstalige landen met graden Fahrenheit wordt gewerkt.
    1. Op de temperatuurschaal van Celsius zie je ook getallen onder 0. Hoe worden die getallen geschreven?
    2. Wat betekent het als de temperatuur buiten –6°C is?
    3. De temperatuurschaal van Fahrenheit lijkt geen getallen onder 0 te kennen. Is dat ook zo?

  2. Grote delen van Nederland liggen onder de zeespiegel. Om de hoogte van het land te meten is het (Normaal Amsterdams Peil) ingevoerd: een hoogteschaal waarbij 0 ongeveer overeen komt met het gemiddelde zeeniveau.
    1. In de Wieringermeerpolder zijn plaatsen die 4,5 m onder zeeniveau liggen. Hoeveel m NAP hoort daar bij?
    2. Het laagste punt van Nederland ligt op 6,76 meter onder het NAP in Nieuwerkerk aan den IJssel. Met welk getal geef je dat aan?
    3. Dicht bij het drielandenpunt op de Vaalserberg bevindt zich het hoogste punt van het Nederlandse vasteland op 322,20 m boven NAP. Hoeveel hoger is dat dan het laagste punt van Nederland?

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Wat is negatief? > Uitleg

In de Uitleg kun je nalezen wat negatieve getallen zijn en waar ze voor komen.

Opgaven

  1. Je ziet hier negen getallen:

    7  –1  3,5  –4  –0,5  1  –3  4

    1. Teken een getallenlijn zoals in de Uitleg en geef daarop deze negen getallen aan.
    2. Welke van deze negen getallen zijn negatief?
    3. Welke van deze negen getallen zijn elkaars tegengestelde?
    4. Hoeveel verschil is er tussen –20 en 20?

  2. Vul de ongelijktekens < en > op de juiste plaats in:
    1. 20 ... –4
    2. –6 ... 6
    3. 3 ... –2
    4. –3 ... –2

  3. Het is op een winterse dag om 16:00 uur nog 2°C. Om 20:00 uur vriest het al 5 graden.
    1. Hoe geef je de temperatuur om 20:00 uur aan?
    2. Hoeveel graden is de temperatuur gedaald?

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Wat is negatief? > Voorbeeld 1

In Voorbeeld 1 zie je dat je op de rekenmachine een speciaal negatiefteken hebt om negatieve getallen in te voeren. Bij het opschrijven van negatieve getallen en in de opgaven wordt er vaak geen verschil gemaakt tussen het negatiefteken en het bewerkingsteken voor aftrekken, beide zijn een minteken. Maar je rekenmachine maakt wel verschil! Het negatiefteken wordt daarop vaak met een wat kleiner en hoger minteken aangegeven, of met de knop die je in het voorbeeld aantreft.

Opgaven

  1. Pak je rekenmachine er maar even bij.
    1. Bereken `0 - 6`. Welk antwoord geeft je rekenmachine?
    2. Voer –6 in. Staat er nu hetzelfde in je rekenmachine als bij a?
    3. Het verschil tussen `6` en –6 bereken je door –6` - 6` door de rekenmachine te laten bepalen. Wat komt er uit?
    4. En wat levert `6 - `–6 op?

  2. Je rekenmachine kan met negatieve getallen rekenen. Je moet daarbij wel steeds goed letten op het verschil tussen het negatiefteken en het bewerkingsteken voor aftrekken. In de praktijk schrijf je ze meestal hetzelfde, maar de rekenmachine maakt wel verschil.
    1. Voer maar eens `6 - -6` in met twee keer achter elkaar de mintoets voor aftrekken. Als het goed is gaat de rekenmachine protesteren.
    2. `6 - ^(-)6` rekent de machine daarentegen goed uit (eerst het aftrekteken, dan het negatiefteken). Ga dat na.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Negatieve getallen > Wat is negatief? > Voorbeeld 2

Ook in een assenstelsel zijn negatieve getallen handig. Want je moet soms vanaf een punt midden op het vlak beginnen te tellen...

Opgaven

  1. Gebruik de applet van Voorbeeld 2.
    1. Maak de in de tekst aangegeven punten in het assenstelsel.