Gelijke hoeken

Verkennen

Opgaven

1. Hier zie je de tafelbladen van vier hoektafeltjes die precies in de hoeken van Marieke's kamer passen. Marieke wil elk blad zo schilderen dat er twee helften ontstaan met een verschillende kleur.
   Hoe krijgt ze dat voor elkaar?
   


2. De vier tafelbladen passen tegen elkaar.
   1. Hoe groot is de hoek die de vier tafelbladen dan maken?
   2. Welke twee tafelbladen maken samen een hoek van 180°?
   3. Tafelblad I heeft een hoek van 101°. Van welke tafeltje weet je nu ook de hoek?

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Gelijke hoeken > Uitleg

Soms wil je een hoek in twee gelijke hoeken delen. Je meet hem dan eerst op en deelt het aantal graden in twee gelijke delen.

Opgaven

3. Hier zie je een hoekpunt `A` met twee hoeken `/_ A_1` en `/_ A_2` die samen een gestrekte hoek vormen.
   
   
   
   
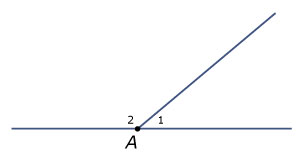
   1. Meet `/_ A_1` op en teken de deellijn van `/_ A_1`.
   2. Hoe groot is `/_ A_2`?
   3. Teken de deellijn van `/_ A_2`.
   4. Welke hoek maken de twee getekende deellijnen met elkaar? Moet je die hoek opmeten?


4. Teken `Delta ABC` met `AB = 6` cm, `/_ A = 50`° en `/_ B = 70`°.
   1. Teken de deellijn van `/_ A`.
   2. Teken ook de deellijnen van `/_ B` en `/_ C`.
   3. Valt je iets op?

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Gelijke hoeken > Voorbeeld 1

Je ziet een voorbeeld van een situatie waarin hoeken gelijk zijn. Het gaat om overstaande hoeken.

Opgaven

5. Bekijk de figuur in het voorbeeld. Je kunt `/_ A_1` aanpassen door in de applet de rode punten te verplaatsen.
   1. Stel `/_ A_1` in op 37°. Hoe kun je dan de grootte van `/_ A_2` weten?
   2. Leg nu uit waarom `/_ A_3 = /_ A_1`.
   3. Leg ook uit waarom `/_ A_4 = /_ A_2`.


6. Bekijk de figuur hiernaast.
   1. Waarom is nu `/_ A_1 != /_ A_3`?
   2. Stel je voor dat `/_ A_1 = 56`°. Van welke hoek weet je dan ook de grootte? Hoe groot is die hoek?

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Gelijke hoeken > Voorbeeld 2

Hier gaat het om gelijke F-hoeken en Z-hoeken.

Opgaven

7. Bekijk de applet in het voorbeeld.
   1. Teken zelf zo'n figuur met twee evenwijdige lijnen gesneden door een derde lijn en de snijpunten `A` en `B`.
   2. Nummer de hoeken om `A` en `B` op dezelfde manier.
   3. Met welke hoek vormt `/_ A_2` een stel F-hoeken?
   4. Met welke hoek vormt `/_ A_2` een stel Z-hoeken?
   5. Leg uit waarom `/_ A_4 = /_ B_2`.


8. Bekijk de volgende figuur. De lijnen `l` en `m` zijn evenwijdig, evenals de lijnen `k` en `q`.
   
   
   
   
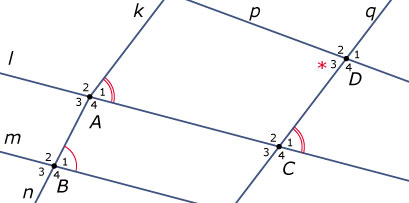
   1. Waarom is `/_ A_1 != /_ B_1`?
   2. Waarom is `/_ A_1 = /_ C_1`?
   3. Waarom is `/_ C_1 != /_ D_3`?
   4. Welke hoek is ook gelijk aan `/_ A_1`? En waarom?
   5. Stel dat `/_ A_1 = 60`°. Van welke hoeken weet je nu ook hoe groot ze zijn? Schrijf ze allemaal op.


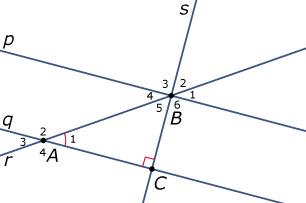
9. In deze figuur zijn de lijnen `p` en `q` evenwijdig. Verder is `/_ A_1 = 43`°. Bereken alle andere genummerde hoeken in deze figuur.
   
   
   
   

Oefenen

10. Teken van deze hoeken de deellijn.
    
    
    
    


11. Hier zie je een plattegrond van de kamer van Marieke. Ze krijgt nieuwe vloerbedekking. Dat zijn vloertegels van 50 cm bij 50 cm. Om ze in de juiste vorm te snijden meet ze de hoeken van haar kamer die niet recht zijn. Waarom hoeft ze maar twee hoeken te meten? Welke twee bijvoorbeeld?
    
    
    
    


12. Teken `Delta ABC` met `/_ A = 50`°, `AB = 6` cm en `AC = 4` cm.
    1. Laat zien dat de bissectrices van de hoeken van deze driehoek door één punt `S` gaan.
    2. Om punt `S` zitten nu zes hoeken. Geef met gelijke tekentjes aan welke van die hoeken gelijk zijn.


13. Bereken in deze figuur alle hoeken als de lijnen `p` en `q` evenwijdig zijn en gegeven is: `/_ B_4 = 40`° en `/_ B_6 = 25`°.
    
    
    
    

Toepassen

14. Doelman

    Het uitlopen van de doelman op een doorgebroken speler die op doel wil schieten is een mooi voorbeeld van het toepassen van een deellijn. Lees

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Gelijke hoeken > Toepassen

    Bij een voetbalwedstrijd heeft een speler vanaf de punt van het strafschopgebied een vrije schietkans op doel. De keeper komt uit zijn doel om het scoren te bemoeilijken. Hoe moet hij uitlopen? In de Wikipedia bij "voetbalveld" vind je de afmetingen van een voetbalveld.
    
    



15. Parallellogram

    Gegeven is een parallellogram `ABCD` met `AB = 6` cm en `AD = 4` cm. Verder is `/_ BAD = 50`°
    1. Teken dit parallellogram.
    2. Leg uit, hoe je met behulp van F-hoeken de andere hoeken van dit parallellogram kunt berekenen.