Diagonaalvlakken

Verkennen

Opgaven

1. Hier zie je pakjes Chocomel. Neem aan dat elk van die pakjes de vorm heeft van een balk van 5,5 cm bij 4,0 cm bij 9,5 cm. Er zit 200 mL Chocomel in.
   1. Kan er wel 200 mL Chocomel in zo'n pakje?
   2. In elk van die pakjes zit vlak bij een hoekpunt van het bovenvlak een plek waar je het rietje kunt insteken. Hoe lang moet zo'n rietje minstens zijn?

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Diagonaalvlakken > Uitleg

Lees na wat je verstaat onder een diagonaalvlak en een lichaamsdiagonaal in een ruimtelijke figuur.

Opgaven

2. Voor de balk `ABCD.EFGH` geldt `AB = 5` cm, `BC = 3` cm en `CG = 2` cm.
   1. Teken deze balk. Zet de letters in de juiste volgorde bij de hoekpunten.
   2. Is `ABFE` een diagonaalvlak van de balk? Waarom wel/niet?
   3. Is `ABGH` een diagonaalvlak van de balk? Welke vorm heeft vierhoek `ABGH`?
   4. Welke twee lichaamsdiagonalen liggen in `ABGH`?
   5. Waarom is `BG` geen lichaamsdiagonaal?


3. Hier zie je een prisma. `ABCD.EFGH` is een kubus met ribben van 4 cm, punt `K` ligt 7 cm boven het midden van `AB` en punt `L` ligt 7 cm boven het midden van `CD`.
   1. Is vierhoek `ADLK` een diagonaalvlak van dit prisma? Welke vorm heeft deze vierhoek?
   2. Is vijfhoek `DBFTH` een diagonaalvlak van dit prisma? Waar ligt dan punt `T`?
   3. `P` is met midden van `AB`. Vierhoek `KPCG` is geen diagonaalvlak van het prisma. Waarom niet?


4. Van piramide `ABCD.T` is het grondvlak `ABCD` een vierkant met zijden van 4 cm. De top `T` van de piramide ligt 6 cm boven het snijpunt `S` van de diagonalen van `ABCD`.
   1. Teken deze piramide.
   2. Waarom zijn de genoemde diagonalen geen lichaamsdiagonalen?
   3. Waarom heeft deze piramide geen lichaamsdiagonalen?
   4. Bestaan er piramides die lichaamsdiagonalen hebben?
   5. Heeft deze piramide wel diagonaalvlakken? Zo ja, hoeveel dan?

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Diagonaalvlakken > Voorbeeld 1

In dit voorbeeld zie je alle diagonaalvlakken en alle lichaamsdiagonalen van een balk.

Opgaven

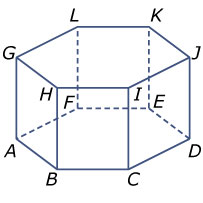5. Hier zie je een zeszijdig prisma.
   1. Hoeveel verticale diagonaalvlakken heeft het prisma? Welke vorm hebben die allemaal?
   2. Hoeveel diagonaalvlakken heeft het prisma verder nog? Welke vorm hebben die diagonaalvlakken?
   3. Hoeveel lichaamsdiagonalen heeft het prisma?


6. Bij de vorige opgave heb je wellicht vooral de figuur gebruikt. Dat is in Voorbeeld 1 voor de balk ook zo gedaan. Toch kun je het aantal diagonaalvlakken en het aantal lichaamsdiagonalen beredeneren vanuit het aantal ribben en het aantal hoekpunten van de figuur.
   1. Hoe kun je vanuit het aantal hoekpunten van de balk het aantal lichaamsdiagonalen beredeneren?
   2. Beredeneer op dezelfde manier het aantal lichaamsdiagonalen van het prisma in de vorige opgave.
   3. Hoe kun je het aantal diagonaalvlakken van een balk beredeneren vanuit het aantal ribben van de balk?
   4. Beredeneer op dezelfde manier het aantal diagonaalvlakken van het prisma in de vorige opgave.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Diagonaalvlakken > Voorbeeld 2

In dit voorbeeld zie je hoe je door diagonaalvlakken op ware grootte te tekenen lengtes van diagonalen (en andere lijnstukken) in ruimtelijke figuren kunt bepalen door meten.

Opgaven

7. Gebruik de balk van opgave 2. Je wilt de lengte van lichaamsdiagonaal `AG` bepalen.
   1. In welke diagonaalvlakken ligt `AG`?
   2. Om zo'n diagonaalvlak op ware grootte te tekenen moet je eerst een geschikt zijvlak op ware grootte tekenen. Teken beide op ware grootte.
   3. Bepaal de lengte van lichaamsdiagonaal `AG` in mm nauwkeurig.


8. Bepaal door meten de lengte van een diagonaal in een grensvlak en van een lichaamsdiagonaal in een kubus met ribben van 1 cm.
   


9. Een pakje Chocomel heeft de vorm van een balk van van 5,5 cm bij 4,0 cm bij 9,5 cm.
   Hoe lang (in mm nauwkeurig) moet het rietje minstens zijn?
   


10. Hier zie je het prisma van opgave 3 nog eens. `ABCD.EFGH` is een kubus met ribben van 4 cm, punt `K` ligt 7 cm boven het midden van `AB` en punt `L` ligt 7 cm boven het midden van `CD`.
    1. Teken diagonaalvlak `ADLK` op ware grootte en bepaal door meten de lengte van `AL`.
    2. Bepaal door meten de lengte van lijnstuk `KG`. Licht je antwoord toe met tekeningen.
    3. Het dak van dit "huisje" bestaat uit de vierhoeken `KFGL` en `EKLH`. Bereken de oppervlakte van dit dak in cm² op één decimaal nauwkeurig.


11. Van piramide `ABCD.T` is het grondvlak `ABCD` een vierkant met zijden van 4 cm. De top `T` van de piramide ligt 6 cm boven het snijpunt `S` van de diagonalen van `ABCD`. Je wilt een uitslag van deze piramide maken.
    1. Teken het grondvlak van de piramide op ware grootte en meet de lengte van `AC`.
    2. Teken diagonaalvlak `TAC` op ware grootte en bepaal de lengte van de ribbe `AT` van de piramide.
    3. Hoe kun je nu met behulp van je passer de uitslag afmaken? Maak hem zo nauwkeurig mogelijk af.

Oefenen

12. Je ziet hier zes keer dezelfde balk van 5 bij 4 bij 4 cm getekend.
    
    
    
    
    1. Teken in elke figuur een ander diagonaalvlak.
    2. Hoeveel echt verschillende diagonaalvlakken zijn er?
    3. Teken de echt verschillende diagonaalvlakken op ware grootte en ga na dat in alle deze figuren de lichaamsdiagonaal van de balk hetzelfde is.
    4. Als de balk van hout is en je zaagt hem langs alle zes de diagonaalvlakken door, hoeveel delen heb je dan na het zagen?
    5. Maak een uitslag van één zo'n deel van deze balk.


13. De minimale afmetingen van een schoollokaal zijn 7,2 m bij 7,2 m bij 3 m. Ga uit van een schoollokaal dat de vorm van een balk heeft. Hoe lang kan de langste paal zijn die nog in dit lokaal past?
    


14. Van een vierzijdige piramide zijn alle ribben 6 cm.
    1. Teken een uitslag van deze piramide.
    2. Berereken de totale oppervlakte van deze piramide, dus de oppervlakte van alle grensvlakken samen. Licht je antwoord toe.


15. In dit prisma is een diagonaalvlak getekend. Het prisma is 5 cm hoog en het grondvlak is er op ware grootte naast getekend.
    
    
    
    
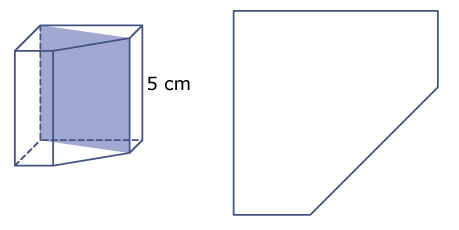
    1. Hoeveel diagonaalvlakken van dit prisma hebben de vorm van een rechthoek?
    2. Teken het kleinste rechthoekige diagonaalvlak op ware grootte.
    3. Hoe lang is de kortste lichaamsdiagonaal in dit prisma?
    4. Hoeveel echt verschillende diagonaalvlakken heeft dit prisma?

Toepassen

16. Regelmatige lichamen

    Bekijk de vijf regelmatige lichamen op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Diagonaalvlakken > Toepassen

    Beredeneer van elk van deze vijf lichamen hoeveel diagonaalvlakken en hoeveel lichaamsdiagonalen er zijn.
    



17. Legertent

    Hier zie je een legertent met een vloer (grondzeil) van 5 m breed en 8 m lang. De tent heeft de vorm van een prisma. De schuine ribben van de voorkant en de achterkant van de tent zijn 2,06 m. Zie voor verdere afmetingen de figuur, de nok van de tent zit boven het midden van het grondvlak.
    
    
    
    
    1. Teken de voorkant van de tent op schaal 1:100. (Gebruik je passer.)
    2. Bereken de totale oppervlakte aan tentdoek, zonder het grondzeil. Laat duidelijk zien welke metingen je daarvoor moet verrichten.
    3. Bereken de inhoud van de tent.