Inhoud

Verkennen

Opgaven

1. Dit is een exemplaar van de "kubus van Rubik", bedacht door de Hongaarse architect en ontwerper Ernö Rubik. Zie ook rubiks.com.
   Uit hoeveel kleine kubussen bestaat hij?
   (Let op: er is geen middelste kubus!)
   

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Inhoud > Uitleg

Om te kunnen bepalen hoeveel er in een ruimtelijke figuur past bereken je het aantal eenheidskubusjes dat er in past. Je krijgt dan de inhoud of het volume van het lichaam.

Opgaven

2. Gegeven is een balk `ABCD.EFGH` met `AB = 6`, `BC = 4` en `CG = 3` eenheden.
   1. Bereken de inhoud van deze balk.
   2. Het prisma `ABC.EFG` is een halve balk. Hoeveel bedraagt de inhoud van dit prisma?
   3. Punt `M` is het midden van `EF` en punt `N` is het midden van `GH`. Hoeveel bedraagt de inhoud van prisma `BFM.CGN`?


3. Gegeven is een balk `ABCD.EFGH` met `AB = 6,5`, `BC = 4,2` en `CG = 3,1` eenheden.
   1. Je moet nu ook met delen van eenheidskubussen rekenen. Waarom?
   2. Bereken de inhoud van deze balk.
   3. Het prisma `ABC.EFG` is een halve balk. Hoeveel bedraagt de inhoud van dit prisma?
   4. Stel dat elke eenheidskubus een inhoud heeft van 1 cm³ (kubieke centimeter). Hoeveel bedraagt dan de inhoud van het prisma?

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Inhoud > Voorbeeld 1

Veel ruimtelijke figuren kun je verdelen in balken en halve balken. En zo kun je dan de inhoud berekenen.

Opgaven

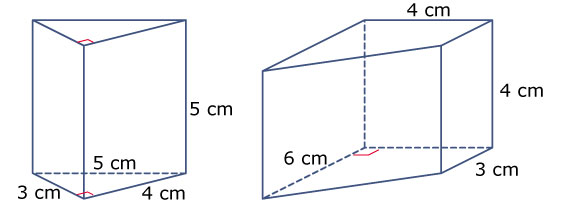
4. Je ziet hier een tweetal prisma's. Laat zien hoe je ze kunt verdelen in balken en halve balken en bereken zo de inhoud van beide prisma's. (Let op de rechte hoek tekens!)
   
   
   
   

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Inhoud > Voorbeeld 2

Zeker als de afmetingen van een balk of een prisma geen gehele getallen zijn is het handig om met de formule uit Voorbeeld 2 te werken.

Opgaven

5. Bekijk de figuur in Voorbeeld 2.
   1. Teken het grondvlak van het prisma zoals het in werkelijkheid is. Neem aan dat de afmetingen in centimeter zijn.
   2. Laat zien dat de figuur in een rechthoek en een halve rechthoek is te verdelen en bereken zelf de oppervlakte van het grondvlak.
   3. Waarom geldt nu voor de inhoud van dit prisma: inhoud prisma = opp.grondvlak × hoogte?
   4. En waarom geldt dit voor alle prisma's?


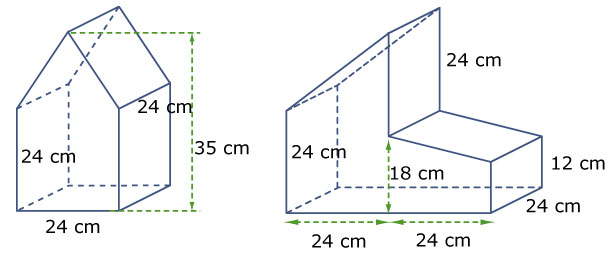
6. Het grondvlak van een prisma is lang niet altijd het onderste vlak. Bepaal van de volgende prisma's eerst wat het grondvlak is en wat de hoogte is en bereken daarmee de inhoud. Alle vierhoekige grensvlakken zijn rechthoeken, verder zijn er rechte hoeken aangegeven.
   
   
   
   


7. Hiernaast zie je een stapel van 50 euromunten. Elke euromunt is 0,233 cm dik en heeft twee cirkelvormige kanten met een oppervlakte van elk ongeveer 4,25 cm².
   1. Hoe hoog is een stapel van 50 euromunten?
   2. Leg uit dat de inhoud van zo'n stapel euromunten gelijk is aan `4,25 xx 11,65` cm³.
   3. Leg uit waarom je het principe inhoud = opp.grondvlak × hoogte kunt toepassen op alle ruimtelijke figuren die er uit zien als een stapel van dezelfde vlakjes boven elkaar.
   
   


8. Dit blik is een cilinder met een grondvlak van 78,5 cm² en een hoogte van 8 cm.
   Hoeveel bedraagt de inhoud van dit blik?
   
   
   
   

Voorbeeld 3

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Inhoud > Voorbeeld 3

En hoe bereken je het volume van voorwerpen die niet de vorm van een prisma of een cilinder of een balk hebben?

Opgaven

9. Een voorwerp wordt ondergedompeld in een grote kubusvormige bak water die met zijn grondvlak op een horizontaal tafelblad staat.
   Deze bak heeft ribben met een lengte van 20 cm.
   Voordat het voorwerp erin wordt gelegd staat het water 10 cm boven het grondvlak van de kubus. Daarna staat het water 13 cm boven het grondvlak. Hoeveel cm³ bedraagt de inhoud van dit voorwerp?
   


10. In een maatbeker worden vaak maatstreepjes gebruikt om aan te geven hoeveel vloeistof er in zit.
    Waarom zitten in een cilindervormige maatbeker de maatstreepjes op gelijke afstanden van elkaar en in een kegelvormige maatbeker niet?
    Moeten bij een kegelvormige maatbeker de maatstreepjes dichter bij elkaar zitten als de opening wijder wordt of juist verder van elkaar?
    
    

Oefenen

11. Bereken de inhoud van deze prisma's. De grondvlakken van beide figuren zijn rechthoekig en alle verticale ribben staan daar loodrecht op.
    
    
    
    


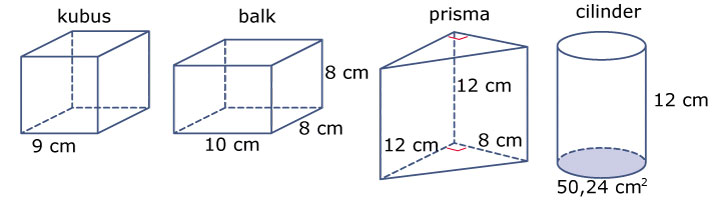
12. Welke van deze figuren heeft de grootste inhoud?
    
    
    
    


13. Een pakje drinken heeft de vorm van een balk met een lengte van 7,0 cm, een breedte van 3,5 cm en een hoogte van 12,5 cm.
    Hoeveel drinken gaat er in dit pakje?
    


14. Een ijzeren staaf heeft de vorm van een cilinder met een dwarsdoorsnede van 6,28 cm² en een lengte van 1,20 m.
    Elke cm³ ijzer weegt 7,9 gram.
    Hoe zwaar is deze staaf?
    


15. Kubus `ABCD.EFGH` heeft ribben van 4 cm. Punt `P` is het midden van `AB` en punt `R` is het midden van `EF`. Punt `Q` ligt op `CD` zo, dat `QD = 3` cm. Punt `S` ligt op `GH` zo, dat `SH = 3` cm.
    1. Teken de kubus `ABCD.EFGH` met de punten `P`, `Q`, `R` en `S`.
    2. `APQD.ERSH` is een prisma. Welk vlak is het grondvlak?
    3. Bereken de inhoud van prisma `APQD.ERSH`.


16. Je ziet een foto van een huis.