Uitslagen

Verkennen

Opgaven

1. Hier zie je een bouwplaat van een Volkswagen Transporter afkomstig van Cheehtahtravel.nl.
   
   
   
   Even printen, uitknippen en je hebt een busje...
   Waar zou je misschien nog extra plakrandjes willen hebben?
   

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Uitslagen > Uitleg

Om ruimtelijke figuren zelf te kunnen maken van een stuk (stevig) papier of karton heb je een bouwplaat nodig. Dat is een uitslag van de figuur met op handige plaatsen plakranden.

Opgaven

2. Gegeven is een balk `ABCD.EFGH` met `AB = 5` cm, `BC = 3` cm en `CG = 4` cm.
   1. Maak eerst een tekening van de balk.
   2. Zet de letters op de juiste plaats bij de balk.
   3. Teken nu een uitslag van deze balk.
   4. Zet ook in de uitslag de letters op de goede plaats. Denk er om dat sommige letters op meerdere plaatsen komen te staan.


3. In de voorgaande opgaven heb je de uitslag van een balk getekend.
   Maak er een bouwplaat van door plakrandjes toe te voegen. Doe dat zo, dat de uiteindelijke balk aan alle kanten dicht is.
   

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Uitslagen > Voorbeeld 1

In dit voorbeeld zie je hoe je de uitslag van een piramide kunt maken als de lengtes van alle ribben bekend zijn.

Opgaven

4. Van een piramide `ABCD.T` geldt dat `AB = 4` cm, `BC = 4` cm, het grondvlak een vierkant is en `AT = BT = CT = DT = 8` cm.
   1. Teken een uitslag van deze piramide.
   2. Knip je uitslag uit en zet de piramide in elkaar. (Maak eventueel eerst plakrandjes!)
   3. Hoe hoog zit `T` boven het grondvlak?


5. Van een regelmatige vierzijdige piramide `ABCD.T` is het grondvlak een vierkant van `4` cm bij `4` cm. De top `T` zit `6` cm boven het midden van het grondvlak.
   1. Maak eerst een tekening van de piramide.
   2. Welk probleem doet zich voor als je een uitslag van deze piramide wilt tekenen?
   3. Kun je daarvoor een oplossing bedenken? Teken dan de uitslag van deze piramide.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Uitslagen > Voorbeeld 2

In dit voorbeeld zie je enkele "uitslagen". Sommige zijn goed, andere niet.

Opgaven

6. Bekijk de figuren in Voorbeeld 2.
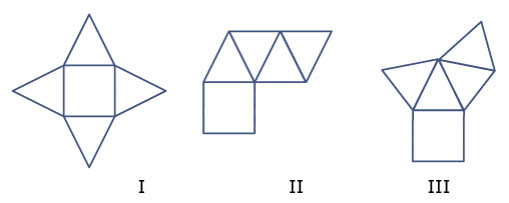
   Leg uit waarom de uitslagen I en IV geen goede uitslagen zijn.
   


7. Welke van deze figuren zijn goede uitslagen van een regelmatige vierzijdige piramide?
   
   
   
   


8. Christien heeft geprobeerd om van een cilinder een uitslag te maken. Hier zie je haar tekening.
   1. Wat is er fout aan deze figuur?
   2. Verbeter de uitslag die Christien heeft gemaakt.

Oefenen

9. Op een normale kubusvormige dobbelsteen staan op elk grensvlak ogen. Het aantal ogen varieert van 1 tot en met 6 en op tegenover elkaar liggende grensvlakken is het aantal ogen samen altijd 7.
   Teken twee verschillende uitslagen van zo'n dobbelsteen.
   


10. Teken een uitslag van een regelmatige vierzijdige piramide waarvan alle ribben 5 cm lang zijn.
    


11. Van deze kubus is een stuk afgezaagd. De hoekpunten van het driehoekige grensvlak zijn precies de middens van de ribben van de oorspronkelijke kubus.
    
    
    
    Teken een uitslag van deze kubus.
    


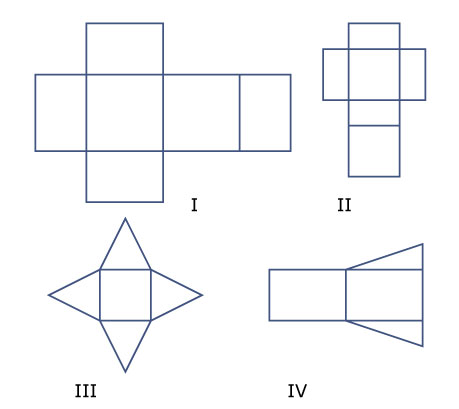
12. Welke van de volgende uitslagen zijn goed?
    
    
    
    


13. Dit is een driezijdig prisma. De twee driehoeken hebben zijden van 4 cm. De drie rechthoeken hebben zijden van 4 cm en 6 cm.
    
    
    
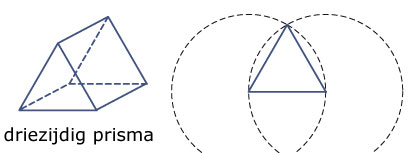
    Je wilt van dit prisma een uitslag maken. Er is al een begin gemaakt.
    1. Teken zelf een driehoek met zijden van 4 cm. Gebruik daarbij je passer.
    2. Zet nu op elk van de zijden van die driehoek rechthoeken van de juiste afmetingen.
    3. Maak vervolgens de uitslag af.

Toepassen

14. Bouwplaten

    Bouwplaten zijn er van allerlei bekende gebouwen, van allerlei voertuigen, vaartuigen, vliegtuigen. Zie

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Uitslagen > Toepassen

    1. Bekijk de bouwplaat goed. Waar vind je op de figuur een bouwplaat van een cilinder?
    2. Ga na, dat de bouwplaat klopt door hem uit te knippen en in elkaar te zetten.
    3. Zoek maar eens of je mooiere bouwplaten kunt vinden. Biijvoorbeeld ook van voorwerpen met gebogen grensvlakken. Zet ze in elkaar!



15. Kubus in de verf

    Hier zie je een paar kubussen die in de verf zijn gedoopt. Teken er telkens een uitslag van waarop je het gekleurde deel van de kubus duidelijk aangeeft.
    
    
    
    



16. Kegel maken

    Het maken van de uislag van een kegel is nog best lastig. Maar het omgekeerde is niet al te moeilijk.
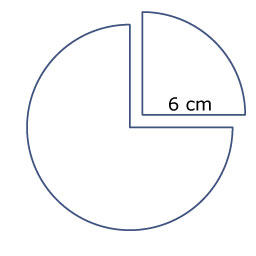
    1. Teken op een stuk stevig papier een cirkel met een straal van 6 cm.
    2. Knip een kwart punt uit deze cirkel, zie figuur.
    3. Maak van beide punten een kegel. Wat is van beide kegels hetzelfde en waarin verschillen ze?
    4. De omtrek van een cirkel is ongeveer 6,28 keer de straal. Laat zien hoe groot van beide kegels de straal van de grondcirkel zou moeten zijn. Meet na of dit klopt.
    5. Bedenk een manier om een kegel te maken met een grondcirkel met een diameter van 10 cm en waarvan de top 10 cm boven het middenlpunt van de grondcirkel zit.