Ruimtelijke figuren tekenen

Verkennen

Opgaven

1. Van een kubus zijn alle ribben even lang.
   
   
   
   
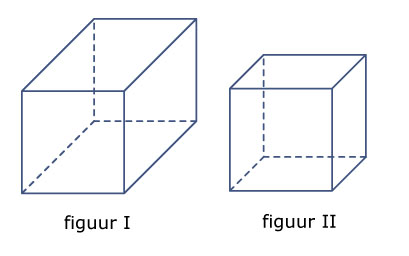
   1. Welke van deze twee figuren zou dus de kubus moeten zijn? (Meet de ribben na.)
   2. Waarom lijkt de andere meer op een kubus?


2. Teken een goed gelijkende kubus op roosterpapier.
   

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Ruimtelijk tekenen > Uitleg

Bij het tekenen van ruimtelijke figuren op een plat vlak (zoals een stuk roosterpapier) moet je er rekening mee houden dat ze ook echt moeten "lijken". Daarom teken je de lijnstukken die "naar achteren" lopen korter dan ze in werkelijkheid zijn. Gebruik wel het rooster!

Opgaven

3. Hier zie je het begin van een balk `ABCD.EFGH` van 5 cm lengte, 4 cm breedte en 3 cm hoogte op een cm-rooster.
   
   
   
   
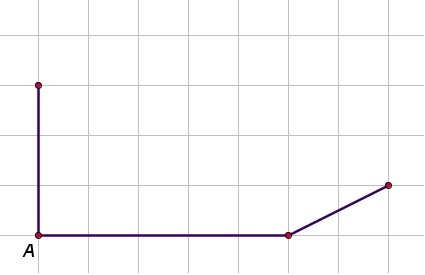
   1. Maak de figuur af. (Denk om het stippelen van de lijnen die je in werkelijkheid niet kunt zien als de balk een massief lichaam is.)
   2. Zet de letters op de juiste plaats bij de balk.
   3. Welke ribben zijn even lang als ribbe `BC`?
   4. Waarom zijn ribbe `BC` en alle ribben die even lang zijn niet op ware grootte getekend?
   
   


4. Maak de volgende figuren af door de ontbrekende lijnstukken te tekenen en op een logische manier letters bij de hoekpunten te zetten. Sommige lijnstukken moeten worden gestippeld.
   
   
   
   

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Ruimtelijk tekenen > Voorbeeld 1

In dit voorbeeld zie je hoe je een balk met gegeven afmetingen tekent op roosterpapier.

Opgaven

5. Voor een balk `ABCD.EFGH` geldt, dat `AB = 6` cm, `BC = 2` cm en `AE = 3` cm.
   Teken deze balk op roosterpapier.
   


6. Teken op roosterpapier een kubus `ABCD.EFGH` met ribben van 4 cm.
   Zet er op de juiste manier de letters bij.
   


7. Gegeven is een balk `ABCD.EFGH` met `AB = BC = 4` cm en `AE = 6` cm.
   1. Teken deze balk op roosterpapier.
   2. Teken in het bovenvlak `EFGH` het snijpunt `T` van de diagonalen.
   3. Teken nu piramide `ABCD.T`.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Ruimtelijk tekenen > Voorbeeld 2

In dit voorbeeld zie je hoe je een vierzijdige piramide met gegeven afmetingen tekent op roosterpapier.

Opgaven

8. Voor een vierzijdige piramide `ABCD.T` geldt, dat het grondvlak `ABCD` een rechthoek is met `AB = 6` cm, `BC = 4` cm en dat `T` boven het midden `S` van het grondvlak zit met `TS = 8` cm.
   Teken deze piramide op roosterpapier.
   


9. Gegeven is een regelmatige vierzijdige piramide waarvan het grondvlak zijden van 4 cm heeft en de top 6 cm boven het grondvlak zit.
   1. Teken deze piramide op roosterpapier.
   2. Teken op de zijden van het grondvlak acht punten steeds 1 cm van een hoekpunt af en verbindt deze punten tot een achthoek. Maak van de regelmatige vierzijdige piramide een achtzijdige piramide met deze achthoek als grondvlak en dezelfde top.
   3. Waarom is dit geen regelmatige achtzijdige piramide?

Oefenen

10. Teken een balk `ABCD.EFGH` met `AB = 4` cm, `AD = 3` cm en `AE = 1` cm.
    1. Teken deze balk op roosterpapier. Stippel de onzichtbare ribben.
    2. Zet er de letters bij de hoekpunten.
    3. Uit hoeveel kubussen van 1 cm bij 1 cm bij 1 cm bestaat het?


11. Deze kaars heeft de vorm van een regelmatige vierzijdige piramide met een grondvlak van 6 cm bij 6 cm en een hoogte van 30 cm.
    Teken deze kaars op roosterpapier op schaal 1:2. Stippel de onzichtbare ribben.
    


12. Hier zie je een prisma en een deel van een prisma.
    
    
    
    
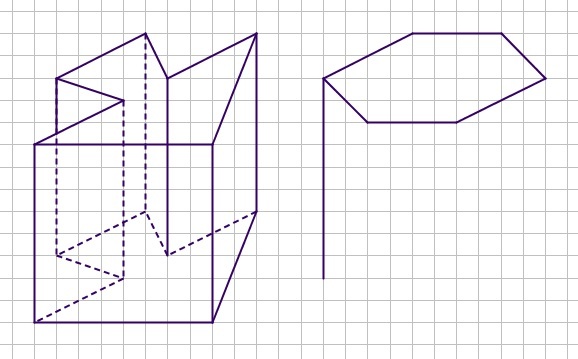
    1. Maak het tweede prisma af. Hoe heet zo'n prisma?
    2. Teken zelf nog een derde prisma.


13. Hier zie je een bol met een diameter van 4 cm. Een cilinder en een kegel hebben dezelfde diameter. De hoogte van de kegel en de cilinder is evenveel als de diameter van de bol.
    Teken beide figuren naast de bol.
    
    
    
    


14. Dit is de "Lümmel" een stoel/poef/bijzettafeltje. Hij bestaat uit twee in elkaar geschoven balken. Teken op roosterpapier zo'n lümmel. Het gaat waarschijnlijk het gemakkelijkst wanneer je hem als bijzettafeltje tekent. Kies de afmetingen zo, dat hij zo goed mogelijk lijkt op het voorbeeld.
    
    
    
    

Toepassen

15. Parallelprojectie

    Vaak worden ruimtelijke figuren in parallelprojectie getekend. Dat betekent dat lijnen die in werkelijkheid evenwijdig zijn dat ook in de tekening zijn. Zie

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Meten en tekenen > Ruimtelijk tekenen > Toepassen

    1. Zijn de figuren die je in dit onderdeel hebt getekend parallelprojecties? Licht je antwoord toe.
    2. Zoek (op internet) voorbeelden van 3D-figuren in parallelprojectie. Laat in je figuren zien dat er inderdaad van parellelprojectie sprake is.
    3. In figuren die lijken op de werkelijkheid is vaak geen sprake van parallelprojectie. Zoek (op internet) foto's van voorwerpen en laat daarin zien dat daarin evenwijdige lijnen niet evenwijdig zijn maar naar elkaar toe lopen.



16. Acrylletters

    Acryl is een doorzichtige kunststof die wel wordt gebruikt voor het maken van grote reclameletters. Hier zie je er voorbeelden van (door de acryl is een kleurstof gemengd).
    
    
    
    Teken de beginletters van je eigen naam als acrylletter.
    



17. 3D figuren in GeoGebra

    In plaats van het tekenen van ruimtelijke figuren met potlood en liniaal of geodriehoek kun je ook gebruik maken van GeoGebra. Dit programma is gratis te downloaden op je pc. Eventueel kun je de onderstaande applet gebruiken.
    
    Sorry, de GeoGebra Applet start niet. Zorg dat Java 1.4.2 (of een nieuwere versie) actief is. (klik hier om Java nu te installeren)