Vlakke figuren

Antwoorden

1. Er zijn vierkanten, rechthoeken, driehoeken, maar ook vierhoeken en vijfhoeken waarvan je waarschijnlijk de naam nog niet weet.
   
2. 1. I rechthoek | II ruit | III driehoek | IV vierkant | V parallellogram | VI rechthoek | VII vlieger
   2. Figuur III.
   3. Drie hoekpunten en drie zijden.
   4. Bij twijfel laten controleren.
3. Een vijfhoek heeft vijf hoekpunten en vijf zijden.
   
4. 10
   
5. 
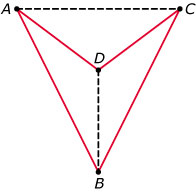
   1. Omdat tussen drie punten die een driehoek vormen niet meer dan drie lijnstukken kunnen worden getrokken en deze lijnstukken precies de zijden van de driehoek vormen.
   2. Omdat tussen vier punten die een vierhoek vormen zes lijnstukken kunnen worden getrokken en daarvan precies vier de zijden van de vierhoek vormen.
   3. Hiernaast zie je een voorbeeld. De stippellijnen zijn de diagonalen.
6. Zie figuur, de diagonalen zijn de stippellijnen.
   
   
   
   
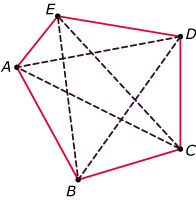
7. Vanuit elk hoekpunt van een vijfhoek kun je vier lijnstukken naar de andere punten trekken. Dat zijn in totaal `(5 xx 4)/2 = 10` lijnstukken (omdat je alle lijnstukken dan twee keer tekent). Vijf daarvan zijn zijden van de vijfhoek, dus er zijn altijd 5 diagonalen.
   
8. Dan zijn er `(10 xx 9)/2 - 10 = 35`.
   
9. 1. Doen. Bij twijfel antwoord laten controleren.
   2. Figuur I is ook een parallellogram. Maar omdat het een parallellogram met loodrecht op elkaar staande zijden is noem je hem liever rechthoek.
10. 1. Doen.
    2. Als het goed is zijn alle zijden even lang.
    3. Ja.
    4. Nee, de zijden moeten dan allemaal even lang zijn.
    5. Dat de aangrenzende zijden recht op elkaar staan.
    6. Nou ja, op zich kan het wel, maar dan in de vorm van een vierkant. Je kunt geen rechthoek maken waarvan niet alle zijden even lang zijn.
    7. De zijden `AB` en `CD` blijven evenwijdig.
    8. Door de zijden `AB` en `CD` ook even lang te maken.
    9. Je maakt dan alle zijden even lang en zorgt ervoor dat aangrenzende zijden loodrecht op elkaar staan.
11. 1. Waar. In elk vierkant staan de aangrenzende zijden loodrecht op elkaar.
    2. Waar. In elk vierkant zijn de zijden even lang.
    3. Onwaar. In een ruit hoeven de aangrenzende zijden niet loodrecht op elkaar te staan.
    4. Waar. Op dit moment kun je dat alleen nog maar nagaan met je geodriehoek. Dit geldt in elke ruit en ook in elke vlieger.
    5. Onwaar voor alle rechthoeken die niet ook een vierkant vormen.
12. 1. 27 als je de grote rechthoeken onder en boven de ruiter te paard ook meetelt.
    2. 1
    3. 14
    4. Dat blijft onzeker, waarschijnlijk maar eentje.
13. 1. I vlieger (met twee loodrechte zijden) | II ruit | III parallellogram | IV rechthoek
    2. Gebruik weer gelijke tekens om gelijke zijden aan te geven en het loodrecht-tekentje voor zijden die recht op elkaar staan.
14. 20
    
15. 1. Als je een driehoek met drie gegeven zijden tekent, krijg je altijd dezelfde driehoek. Bij een vierhoek (of vijfhoek, of...) kun je de figuur dan toch nog vervormen. Denk maar aan een rechthoek die je scheef duwt. De zijden blijven even groot, maar staan niet meer loodrecht op elkaar.
    2. Bekijk de animatie van de constructie van een driehoek.
    3. Bekijk de animatie van de constructie van een driehoek.
    4. Bekijk de animatie van de constructie van een driehoek.
    5. Bekijk de animatie van de constructie van een driehoek.
    6. Doe dat op dezelfde manier.
    7. Oefen wel even, hopelijk ontdek je dat het niet altijd lukt.
    8. Steeds moeten twee zijden samen groter zijn dan de derde zijde. Is dit niet het geval, dan kun je geen driehoek maken.
    9. Doen, je ontdekt vanzelf dat je keuzes hebt.
16. Figuur I: vliegers (blauw), 20-hoekige sterren (groen), 10-hoekige sterren (oranje) en twee soorten zeshoeken.
    Figuur II: driehoeken (blauw, grote en kleinere), vierkanten (blauwgroen), zeshoeken (donkerbruin), twee soorten 8-hoekige sterren en 12-hoekige sterren.
    
17. 4850