
Kort maar krachtig
Verkennen
Opgaven
-
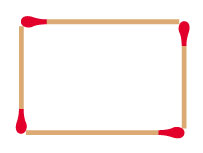
Van twee korte en twee lange lucifers is een rechthoek gelegd.
Omdat je geen afmetingen weet hangt de omtrek van deze rechthoek af van twee variabelen, namelijk lengte korte lucifer en lengte lange lucifer.
- Welke formule krijg je voor de omtrek van deze rechthoek?
- Hoe zou je die formule korter kunnen schrijven?
-
De oppervlakte van de rechthoek uit de vorige opgave hangt van dezelfde variabelen af.
- Welke formule kun je voor de oppervlakte van die rechthoek opstellen?
- Hoe zou je die formule korter kunnen schrijven?
Uitleg
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Uitleg
In dit onderdeel gaat het vooral om het zo kort en overzichtelijk mogelijk schrijven van formules. Dat doe je allereerst door de variabelen niet met woorden maar alleen met een letter aan te geven. En verder gebruik je eigenschappen van rekenbewerkingen. Neem eerst beide pagina's van de Uitleg door.
Opgaven
-
Hier zie je een rechthoek gelegd van twee soorten lucifers. Noem de lengte van de kortste lucifer `k` en die van de langste lucifer `l`.
- Welke formule geldt voor de omtrek `P` van de rechthoek? Schrijf je formule zo kort mogelijk.
- Welke formule geldt voor de oppervlakte `A` van de rechthoek? Schrijf je formule zo kort mogelijk.
- Moet je ook nog iets afspreken over de gebruikte eenheden?
-
Voor het omrekenen van graden Celsius naar graden Fahrenheit bestaat de formule
graden Fahrenheit = `9/5` × graden Celsius + 32
- Schrijf deze formule zo kort mogelijk.
- Bereken `F` als `C = 20`.
- Hoe zou je de voorgaande opdracht in gewoon Nederlands zeggen?
- Wat is het grote voordeel van het gebruik van formules?

Voorbeeld 1
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Voorbeeld 1
www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Voorbeeld 1
Je ziet hoe formules korter kunnen worden geschreven. Met luciferfiguren kun je dit goed oefenen.
Opgaven
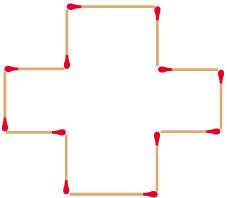 Bekijk de luciferfiguur hiernaast. Neem aan dat alle hoeken recht zijn.
Noem de lengte van de korte lucifer `k` en die van de langere lucifer `l`.
Bekijk de luciferfiguur hiernaast. Neem aan dat alle hoeken recht zijn.
Noem de lengte van de korte lucifer `k` en die van de langere lucifer `l`.
- Schrijf een zo kort mogelijke formule op voor de omtrek `P` van de figuur.
- Bereken `P` als `k = 3` cm en `l = 4` cm met behulp van je formule. Controleer je antwoord met behulp van de figuur.
- Schrijf een zo kort mogelijke formule op voor de oppervlakte `A` van de figuur.
- Bereken `A` als `k = 3` cm en `l = 4` cm met behulp van je formule. Controleer je antwoord met behulp van de figuur.
-
Schrijf bij deze twee rechthoekige luciferfiguren zo eenvoudig mogelijke formules voor de omtrek en de oppervlakte.

Voorbeeld 2
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Voorbeeld 2
www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Voorbeeld 2
In dit voorbeeld zie je formules voor de omtrek en de oppervlakte van een figuur die uit rechte hoeken bestaat.
Opgaven
-
Bekijk de formules in Voorbeeld 2.
- Leg uit hoe je aan de formule voor de omtrek kunt komen.
- Neem `p = 5` en `q = 3` en bereken de omtrek `P`. Controleer je antwoord met behulp van de figuur.
- Leg uit hoe je aan de formule voor de oppervlakte kunt komen.
- Neem `p = 5` en `q = 3` en bereken de oppervlakte `A`. Controleer je antwoord met behulp van de figuur.
-
Bij de volgende uitdrukkingen kun je je voorstellen dat ze de omtrek of de oppervlakte van een rechthoekige luciferfiguur zijn.
Schrijf ze zo eenvoudig mogelijk.
- `a + 4 * b + a + 3 * a + 2 * b`
- `a * b + 2 * a * a + 3 * a * b + a * a`
- `5 * p + 3 * p + 2 * q + p + 6 * q`
- `p * p + 5 * p * q + p * p + p * q`
Voorbeeld 3
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Voorbeeld 3
www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Voorbeeld 3
In dit voorbeeld zie je hoe je ook uitdrukkingen waarbij je minder eenvoudig aan meetkundige figuren kunt denken korter kunt schrijven. Hierbij hoort ook de applet "Slangen". Kennis van negatieve getallen is hierbij nodig.
Opgaven
-
Bekijk Voorbeeld 3. Met de applet "Slangen" kun je het eenvoudiger maken van deze uitdrukkingen zichtbaar maken.
Klik daartoe op het juiste schuifbalkje en beweeg de punt erop met de pijltjestoetsen van je toetsenbord.
- Hieronder zie je de "slang": `a + 2 * b + 3 * a + b - 2 * a`. Laat in de tekening zien dat dit inderdaad gelijk is aan `2 * a + 3 * b`.

- Controleer `a + 2 * b + 3 * a + b - 2 * a = 2 * a + 3 * b` door de getallen `a = 2` en `b = 3` te substitueren.
- Maak nu zelf de "slang": `3 * b - 4 * a - 5 * b + a * 5`. Hoe kun je deze tweede slang korter schrijven?
- Controleer het korter schrijven met `a = 2` en `b = 3`. Waarom betekent dit nog niet dat korter schrijven nu ook zonder meer goed is gedaan?
- Maak de "slang": `-3 * a + b + 5 * a - 4 * b + a`. Schrijf deze uitdrukking zo eenvoudig mogelijk.
- Oefen met een medeleerling (met de applet).
- Hieronder zie je de "slang": `a + 2 * b + 3 * a + b - 2 * a`. Laat in de tekening zien dat dit inderdaad gelijk is aan `2 * a + 3 * b`.
-
Schrijf de volgende uitdrukkingen zo eenvoudig mogelijk.
- `2 * a + 4 * b - a + 3 * a - 2 * b`
- `4 * a - 2 * a + 3 * b + a`
- `5 * p - 3 * p + 2 * q + p - 6 * q`
- `p - 5 * q + p + q`
-
Schrijf de volgende formules zo eenvoudig mogelijk:
- `P = 14 * k + 7 * l - 6 * k - l + 3`
- `A = 5 * a * a - 4 * a * b + 8 * b + 6 * a * b - 4 * b`
- `y = 2 * x * x - 4 * x + 3 * x * x - 3 * x`
- `K = 2 * p + p * 3 - 2 * p * p`
Oefenen
-
Schrijf bij deze twee rechthoekige luciferfiguren zo eenvoudig mogelijke formules voor de omtrek en de oppervlakte. De lengte van de korte lucifer is `p` en die van de lange is `q`.

-
Schrijf de volgende uitdrukkingen zo eenvoudig mogelijk.
- `4 * p + 6 * q - 3 * p + 12 * q`
- `-3 * p - 4 * p + 12 * q + 11 * p`
- `15 * a + 3 * b - 12 * a + b - a`
- `x * 5 + 4 * y - 4 * x`
- `x * x - 4 * x + 2 * x * x - 2 * x`
- `3 * u * v - 2 * v * u + u`
-
Schrijf de volgende formules zo eenvoudig mogelijk.
- ritprijs = 4,50 + 1,25 · aantal klantkilometers.
- omtrek `= 2 * b + l + b + 4 * l + 3 * b`
- oppervlakte `= 2 * l * b + b * b + 1 * b + b * b + 3 * l * b`
- lengte jongen = (lengte moeder + lengte vader + 13) / 2
-
Een leraar berekent het cijfer `c` voor een toets vanuit het aantal punten `p` die een leerling heeft gescoord.
De leraar gebruikt deze formule
`c = p/60 * 9 + 1`
- Hoeveel bedraagt je cijfer als je 40 punten hebt gehaald?
- Waarom kun je voor deze toets maximaal 60 punten halen?
- Maak een grafiek bij deze formule.
- Vanaf hoeveel punten krijg je een 5,5 of hoger?
-
Voor het maken van een fotoboek met eigen digitale foto's betaal je € 9,95 als je niet meer dan 20 foto's hebt.
Voor elke extra foto moet je € 0,15 bijbetalen.
Als `x` het aantal extra foto's is, hoeveel bedragen dan de totale kosten `k` per extra foto?
- Schrijf een bijpassende formule op.
- Neem `x = 15` en bereken `k`.
- Zal `k` ooit minder worden dan 20 cent? Licht je antwoord toe.
Toepassen
Formules in de praktijk
In de praktijk kom je regelmatig formules tegen, vaak in woorden. Ze worden overzichtelijker als je ze korter opschrijft, bijvoorbeeld door letters als variabelen te gebruiken. Zie www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Toepassen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Kort maar krachtig > Toepassen
- Wat stellen de letters `w` en `a` in de formule `w = 6 + a * 0,05` precies voor? Denk ook om de eenheden.
- Waarom kun je deze formule ook schrijven als `w = 0,05 * a + 6`?
- Wat stellen de letters `L` en `u` in de formule `L = 30 - 2 * u` precies voor?
- Hoe kun je deze formule ook schrijven?
- Bekijk de formule `s = v * t`. Leg uit waarom deze formule alleen geldt als `v` de gemiddelde snelheid voorstelt.
- Je gebruikt zo'n formule meestal om juist die gemiddelde snelheid uit te rekenen. Hoeveel bedraagt `v` bij een atleet die de marathon (42 km) aflegt in 2 uur en 20 minuten?
Tsjirpende krekels
Midas Dekkers is bioloog en schrijver van verschillende boeken. Onder andere schrijft hij over het getsjirp van de krekel. Hoe hoger de temperatuur, hoe sneller de krekel tsjirpt. Daarom kun je door het aantal tsjirpen van een krekel te tellen de temperatuur in graden Celsius bepalen. Midas Dekkers gebruikt voor de sneeuwboomkrekel een formule waarbij je moet uitgaan van het gemiddeld aantal tsjirpen per minuut. Je trekt er veertig van af, deelt de uitkomst door zeven en telt er tien bij op.- Noem het gemiddelde aantal tsjirpen per minuut `n`. Welke formule geldt dan voor de temperatuur `T` in °C?
- Een sneeuwboomkrekel tsjirpt 96 keer per minuut. Bereken de temperatuur.
- En hoeveel bedraagt de temperatuur als deze krekel 110 keer per minuut tsirpt?
- Teken een bijpassende grafiek.
- Geef in je grafiek het gedeelte aan dat hoort bij temperaturen van 20°C tot 25°C? Welke waarden voor `n` horen daar ongeveer bij?