Van formule naar grafiek

Verkennen

Opgaven

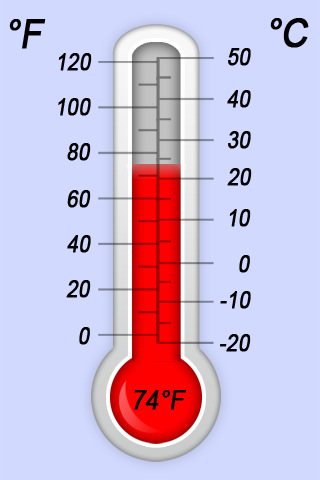
  1. Op de Iphone is deze thermometer als app beschikbaar.`` De temperatuur staat er niet alleen in graden Celsius, maar ook in graden Fahrenheit. Dat komt omdat in veel Engelstalige landen met graden Fahrenheit wordt gewerkt. Voor het omrekenen van de ons vertrouwde graden Celsius naar graden Fahrenheit bestaat de formule

    graden Fahrenheit = `9/5` × graden Celsius + 32

    1. Laat met behulp van deze formule zien dat 32°F bij 0°C hoort.
    2. Bereken ook met de formule hoeveel graden Fahrenheit bij 100°C hoort.
    3. Wat is het voordeel van zo'n plaatje als hiernaast boven een formule? En wat is het nadeel?

  2. Je zou bij de formule voor het omrekenen van graden Celsius naar graden Fahrenheit een grafiek kunnen maken.
    1. Geeft een grafiek bij deze formule dezelfde informatie als de thermometer bij de vorige opgave? Licht je antwoord toe.
    2. Hoe maak je een grafiek bij deze formule?

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Formule naar grafiek > Uitleg

In de Uitleg zie je dat je om een grafiek te maken bij een formule vaak eerst een tabel maakt.

Opgaven

  1. Bekijk de Uitleg.
    1. Wat is het verschil tussen de invoervariabele en de uitkomstvariabele in een formule?
    2. Waarom is hoeveelheid benzine hier een logische keuze voor de invoervariabele?
    3. Ga zelf na dat de tabel klopt en dat de bijbehorende grafiek juist is.
    4. Substitueer het getal 35 voor hoeveelheid benzine. Ga na dat bij de uitkomst een punt van de grafiek hoort.

  2. Gebruik de grafiek en de formule uit de Uitleg
    1. Bepaal met behulp van de grafiek de afstand die deze auto kan rijden als er nog 37 liter benzine in de tank zit.
    2. Bereken deze waarde nauwkeurig met behulp van de formule.
    3. Waarom is in dit geval aflezen uit de grafiek eigenlijk zinvoller dan nauwkeurig berekenen met de formule?

Voorbeeld 1

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Formule naar grafiek > Voorbeeld 1

Je ziet hoe bij de formule weekloon = 6 + aantal folders × 0,05 eerst een tabel wordt gemaakt en dan een grafiek.

Opgaven

  1. Bekijk Voorbeeld 1.
    1. Bereken zelf met de formule het weekloon bij 300 folders.
    2. Substitueer voor aantal folders de waarden 50, 150 en 250 en bereken het weekloon.
    3. Ga na dat de uitkomsten bij b inderdaad punten van de grafiek opleveren.

Voorbeeld 2

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Formule naar grafiek > Voorbeeld 2

In dit voorbeeld gaat het over een opbrandende kaars.

Opgaven

  1. Gebruik de formule in Voorbeeld 2.
    1. Welke variabele is de invoervariabele?
    2. Maak de tabel verder af. Ga door tot de kaars op is.
    3. Teken een grafiek bij deze formule. Welke variabele komt op de verticale as?
    4. Na hoeveel uur is de kaars opgebrand?

  2. Voor het omrekenen van graden Celsius naar graden Fahrenheit bestaat de formule

    graden Fahrenheit = `9/5` × graden Celsius + 32

    1. Maak hierbij een tabel waarbij je voor graden Celsius de waarden 0, 10, 20, ..., 100 kiest.
    2. Teken een bijbehorende grafiek.
    3. De temperatuur van een gezond menselijk lichaam is 37°C. Bereken met de formule hoeveel °F dat is.
    4. Laat zien dat bij het antwoord uit c een punt op de grafiek hoort.

Voorbeeld 3

www.math4all.nl > MAThADORE-basic HAVO/VWO > 1/2 HAVO/VWO > Grafieken en formules > Formule naar grafiek > Voorbeeld 3

In dit voorbeeld zie je een formule voor de kosten per kopie van een winkelier die een kopieermachine wil neerzetten.

Opgaven

  1. Werk met de gegevens in Voorbeeld 3.
    1. Maak een tabel bij deze formule waarbij aantal kopieën de waarden 500, 1000, 1500, 2000, 2500, 3000 heeft.
    2. Teken een bijpassende grafiek.
    3. Waarom is de grafiek geen rechte lijn?
    4. De winkelier wil eigenlijk maximaal € 0,10 per kopie berekenen aan zijn klanten die er gebruik van willen maken. Bepaal door de tabel uit te breiden hoeveel kopieën er dan maandelijks moeten worden gemaakt.

  2. Voor de oppervlakte van een vierkant geldt de formule

    oppervlakte vierkant = zijde × zijde

    waarin zijde de lengte van een zijde van het vierkant is.
    1. Substitueer voor zijde de waarden 0, 1, 2, 3, 4, ..., 10 en maak een tabel bij deze formule.
    2. Teken een bijbehorende grafiek.
    3. Is de grafiek een rechte lijn? Waarom?
    4. Hoe groot is de oppervlakte van een vierkant met zijden van 6,3 eenheden? Geef het bijbehorende punt in de grafiek aan.

Oefenen

  1. Een auto rijdt met één liter benzine 15 km.
    1. Welke formule hoort bij het verband tussen hoeveelheid benzine en afstand?
    2. Vul de tabel verder in:

      hoeveelheid benzine (liter) 01020304050
      afstand (km) 0     

    3. Teken een grafiek bij dit verband.
    4. Waarom is de grafiek een rechte lijn?

  2. Van een rechthoek is de oppervlakte 600. Voor het verband tussen lengte en breedte van deze rechthoek geldt

    lengte = 600 / breedte

    1. Leg uit waarom deze formule correct is.
    2. Maak een tabel bij deze rechthoek. Neem voor breedte de waarden 10, 20, 30, 40, 50, 60 en 100.
    3. Teken een grafiek bij deze formule.
    4. Waarom is deze grafiek geen rechte lijn?

  3. In een stad zijn twee taxibedrijven actief. Ze hebben verschillende tarieven. Je betaalt wel bij beide een vast bedrag als je een taxi laat komen (de voorrijkosten) en daar boven op een bedrag voor elke km die je wordt vervoerd.
    • taxibedrijf A: de voorrijkosten € 7,50 en de prijs per km bedraagt € 2,20.
    • taxibedrijf B: de voorrijkosten € 4,00 en de prijs per km bedraagt € 2,75.
    1. Maak voor beide taxibedrijven een formule voor de ritprijs afhankelijk van het aantal klantkilometers.
    2. Teken bij beide taxibedrijven een bijbehorende grafiek. (Maak dus eerst tabellen.)
    3. Hebben beide grafieken een snijpunt? Wat betekent dit snijpunt?

  4. Een leraar berekent het cijfer voor een toets vanuit de punten die een leerling heeft gescoord. De leraar gebruikt deze formule

    cijfer = aantal punten / 4 + 1

    1. Hoeveel bedraagt je cijfer als je 23 punten hebt gehaald?
    2. Waarom kun je voor deze toets maximaal 36 punten halen?
    3. Maak een tabel bij deze formule. Kies zelf geschikte waarden voor aantal punten.
    4. Maak een grafiek bij deze tabel.
    5. Waarom moet die grafiek eigenlijk uit losse punten bestaan? Hoeveel punten?

  5. De familie Jansen wil in de woonkamer parket op de vloer laten leggen. Ze zien de volgende aanbiedingen in de krant:



    1. Met welke formule kun je de prijs voor parket bij "Superparket" uitrekenen?
    2. Geef ook een passende formule voor "Woonwinkel". Ga er van uit dat de familie Jansen de advertentie inlevert.
    3. De woonkamer van de familie Jansen is ongeveer 4 m bij 5 m. Bij welke van beide winkels zijn ze het goedkoopst uit?

Toepassen

  1. De BMI

    Voor volwassenen is de BMI (Body Mass Index) een getal waaraan je kunt zien of je overgewicht hebt of niet. De BMI wordt zo berekend:

    BMI = gewicht / (lengte × lengte)

    Hierin is de lengte in meter en het gewicht in kg. Bij een BMI tussen de 18,5 en 25 heb je een normaal gewicht.
    1. Kun je bij deze formule een grafiek tekenen?
    2. Hoeveel bedraagt de BMI van een volwassene met een lengte van 180 cm en een gewicht van 80 kg?
    Meestal is iemand's lengte een vast gegeven, maar zijn of haar gewicht niet. Neem bijvoorbeeld een volwassen persoon met een lengte van 180 cm.
    1. Welke formule geldt voor de BMI van deze persoon?
    2. Teken een bijpassende grafiek. Maak eerst een tabel met voor gewicht de waarden 50, 60, 70, 80, 90, 100.
    3. Geef in je grafiek het gedeelte aan dat hoort bij een normaal gewicht. Welke gewichten horen daar bij?
    Als iemand een gewicht van 90 kg heeft, dan denk je al snel aan iemand met overgewicht. Maar dat hoeft niet.
    1. Welke formule voor de BMI geldt voor mensen van 90 kg?
    2. Teken een bijpassende grafiek. Maak eerst een tabel met voor lengte de waarden 1,5; 1,6; 1,7; ...; 2,2.
    3. Geef in je grafiek het gedeelte aan dat hoort bij een normaal gewicht. Welke lengtes horen daar bij?

  2. Grafieken maken met Excel

    Het maken van grafieken is vaak nogal tijdrovend. Het computerprogramma MS-Excel kan je daarbij helpen. Werk daartoe het practicum Grafieken bij tabellen door.
    Je kunt dit goed toepassen bij de opgave over de BMI.