De opkomst van de Oudgriekse beschaving vond omstreeks 600 v.Chr. plaats, dus zo'n 2600 jaar geleden. Tot die vroegste periode behoren beroemde wijsgeren/wiskundigen als Thales van Milete (624 - 547 v.Chr.) en Pythagoras (570 - 500 v.Chr.). Maar de Oudgriekse beschaving duurde nog tot zo'n 300 na Chr. en kende vele andere beroemde wiskundigen zoals Eudoxus, Euklides, Apollonios, Archimedes, Diophantos. In feite is de systematische wiskunde een uitvinding van de Oudgriekse wiskundigen.

Al vroeg werden onder invloed van Pythagoras en zijn filosofische school (in het toenmalige Griekse deel van Zuid-Italië) getallen als zeer belangrijk gezien: ze leken het wezen van de structuur van de wereld te vertegenwoordigen. De Grieken ontwikkelden dan ook de eerste theorie over getallen en de patronen die zich voordeden (even en oneven, deelbaarheid, verhoudingen en breuken, kwadraten, derdemachten). Verder ontdekten zij het bestaan van getallen die niet konden worden geschreven als verhouding van twee gehele getallen (niet als breuk dus), zoals de wortels van getallen die geen kwadraat waren.

De Oudgriekse beschaving was nogal versnipperd in verschillende stadstaten. Ze kenden dan ook verschillende systemen voor het noteren van getallen.
Het oudste systeem (500 - 300 v.Chr.) is het Attische, waarin I stond voor 1 en verder de Griekse hoofdletters werden gebruikt: Ρ = 5 (Ρ van pi, voor 'penta' wat 5 betekent), Δ = 10 (Δ van delta, voor 'deca' wat 10 betekent), Η = 100 (Η van eta, voor 'hekaton' wat 100 betekent, denk aan ons 'hecto'), Γ = 1000 (Γ van chi, voor 'kilioi' wat 1000 betekent, denk aan ons 'kilo') en Μ = 10.000 (Μ van mu, voor 'myrioi'). Met deze symbolen werden getallen gemaakt door ze achter elkaar te schrijven. Daarbij werden soms tekens samengevoegd, 5 ⋅ 100 werd bijvoorbeeld wel gemaakt door het teken voor 100 binnen het teken voor 5 te plaatsen. Het systeem raakte later in onbruik.
Nieuwer (vanaf 300 v.Chr.) was het Ionische systeem, dat algemeen in gebruik werd genomen. In dat systeem werden griekse kleine letters (en nog een paar oudere tekens omdat het Griekse alfabet maar 24 letters kent) gebruikt om getallen aan te duiden:

1 α	2 β	3 γ	4 δ	5 ε	6 ς	7 ζ	8 η	9 θ
10 ι	20 κ	30 λ	40 μ	50 ν	60 ξ	70 ο	80 π	90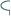
100 ρ	200 σ	300 τ	400 υ	500 φ	600 χ	700 ψ	800 ω	900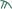
1000 ,α	2000 ,β	3000 ,γ	4000 ,δ	5000 ,ε	6000 ,ς	7000 ,ζ	8000 ,η	9000 ,θ

Ook met deze symbolen werden getallen gemaakt door ze achter elkaar te schrijven. Verder werd het verschil tussen een woord en een getal gemaakt door boven de getallen een streep te trekken, ofwel door een getal aan te geven met een accent:

ιγ' = 13
ξε' = 65
,γψλη' = 3738
,εη' = 5008

Bij een dergelijke schrijfwijze is de plaats van een symbool niet van belang: het Griekse getalstelsel was nog steeds geen positiestelsel zoals het onze. Ook een teken voor nul was daarom niet nodig. Het zou in feite nog een aantal eeuwen duren voordat zo'n symbool werd bedacht.

Er waren twee problemen met dit systeem:

• Ten eerste: hoe schrijf je getallen groter dan 9999?
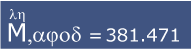  Daarvoor vielen de Grieken in het Ionische systeem terug op het oudere Attische stelsel. Ze gebruikten de Μ voor het aantal 10.000-tallen. Boven dit teken werd dan het Ionische teken gebruikt om aan te geven om hoeveel keer 10.000 het ging. Hiernaast zie je er een voorbeeld van.
• Ten tweede: hoe schrijf je breuken?
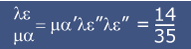  Er werden twee systemen bedacht voor breuken.
  Een breuk als 2/3 werd in het éne systeem geschreven als β'γ"γ". De teller 2 werd als gewoon getal geschreven (met een accent aan het eind), de noemer 3 werd geschreven met twee accenten en bovendien vaak twee keer opgeschreven. Voor 1/2 gebruikte men een speciaal teken: L". En zo werd 1 1/2 geschreven als αL".
  Diophantos gebruikte echter een systeem dat veel lijkt op onze huidige notatie waarin de teller boven de noemer wordt geschreven met een breukstreep ertussen. Hij gebruikte echter geen breukstreep en bovendien schreef hij de noemer boven de teller. In dat geval schrijf je 2/3 door de 3 boven de 2 te zetten, dus de γ boven de β.

Optellen gaat in het Ionische getalstelsel eigenlijk net als in ons huidige stelsel, alleen worden voor de tientallen, honderdtallen, duizendtallen en tienduizendtallen telkens nieuwe symbolen gebruikt. (Omdat alle Griekse letters hieronder op getallen slaan, wordt voor het leesgemaak steeds de accent weggelaten.)
Bijvoorbeeld 21 + 461 + 75 gaat zo:

De optelling is: κα + υξα + οε
Eerst de eenheden bij elkaar: α + α + ε = ζ
Dan de tientallen bij elkaar: κ + ξ + ο = ρν
Het honderdtal ρ dat nu ontstaat gaat tenslotte bij de andere honderdtallen: ρ + υ = χ.
Eindresultaat: χνζ.

Ga na dat deze optelling klopt!
De Grieken schreven voor zo'n optelling de getallen netjes onder elkaar: alle eenheden recht onder elkaar, alle tientallen recht onder elkaar, enzovoort.

Als je twee getallen van elkaar moest aftrekken dan ging dat ook vergelijkbaar met onze huidige methoden.
Bijvoorbeeld 461 – 75 gaat zo:

De aftrekking is: υξα – οε.
Eerst de eenheden van elkaar afhalen: α – ε gaat niet, dus neem je van de ξ een tiental weg: ξ – ι = ν en ια – ε = ς
Nu de tientallen van elkaar afhalen: ν – ο gaat niet, dus neem je een honderdtal van de υ weg: υ – ρ = τ en ρ – ο = ς
Eindresultaat: τςς.

Controleer ook deze aftrekking

Vermenigvuldigen was opnieuw vergelijkbaar met de moderne techniek van 'onder elkaar zetten'. Als je bijvoorbeeld 461 × 75 wilt uitrekenen, dan vermenigvuldig je eerst de eenheden van 461 met 5, dan de tientallen van 461 met 5 en dan de honderdtallen van 461 met 5. Vervolgens tel je dit alles bij elkaar. Daarna vermenigvuldig je eerst de eenheden, dan de tientallen en dan de honderdtallen van 461 met 70 en tel je alles bij elkaar. Je hebt dan twee getallen die je ook weer moet optellen om het eindresultaat te krijgen.
In het Oudgrieks ging dit precies net zo, alleen dan met de door hen gebruikte symbolen.
Probeer deze vermenigvuldiging maar eens, het is nog best een leuke puzzel...

Bij delen moet je de deler herhaaldelijk van het deeltal aftrekken. Hoe vaak dit kan is de uitkomst van de deling. Bijvoorbeeld bij 338/13 kijk je eerst hoe vaak de deler 13 'in de 3 honderdtallen past', dat gaat 23 keer en je houdt nog 300 – 23 × 13 = 1 over. Daarna kijk je hoe vaak 13 'in de 38 + 1 = 39 past', dat gaat precies 3 keer. En dus is 338/13 = 23 + 3 = 26.
In het Oudgrieks kan dit op dezelfde manier, maar met de door hen gebruikte symbolen.

Als een deling niet uit komt (er blijft een ondeelbare rest over) krijg je een breuk. Hoe de Oude Grieken breuken noteerden is al beschreven. Daarnaast kenden zijn het Oud Egyptische systeem van stambreuken, alleen dan in hun eigen letternotatie. Ze konden daarom met breuken net zo rekenen als de Egyptenaren. Sommigen van hen (bijvoorbeeld Ptolemaios in zijn 'Amalgest') gebruikten ook de Babylonische notatie voor breuken: een positiestelsel met 60 als basis. Ook met de Babylonische rekentechnieken waren de Grieken kennelijk bekend.

Voor de Grieken bestonden er alleen gehele getallen boven 0 en verhoudingen van dergelijke getallen (de 'breuken'). Maar de stelling van Pythagoras had voor hen een moeilijk voorstelbaar bijverschijnsel: een rechthoekige driehoek met rechthoekszijden van 1 cm had een schuine zijde (hypothenusa) die niet zo'n getal opleverde. Wij noemen de lengte van die schuine zijde 'wortel 2'. De Oude Grieken ontdekten al dat dit 'getal' geen geheel getal was en ook niet was te schrijven als een verhouding van twee gehele getallen, als een breuk dus. Wij rekenen gewoon met dergelijke wortels, voor de Oude Grieken was dit een geweldig probleem. Zij noemden deze getallen onmeetbare getallen. Ze konden ze wel construeren (m.b.v. een rechthoekige driehoek) maar er mee rekenen ging niet echt. Alleen met meetkundige hulpmiddelen, constructies met passer en liniaal, leek het opereren met dergelijke onmeetbare getallen voorstelbaar. Lees verder in:

• "Van Ahmes tot Euklides", door prof. L.N.H. Bunt, e.a.
• "Mathematical thought from ancient to modern times", door M. Kline.