Fragmenten
menu-onderdelen
Fragmenten - Rekenen in het Oude Egypte

De oudst bekende systemen van getallen noteren en rekenen stammen uit het Oude Egypte en het Oude Mesopotamië. Hier wordt besproken hoe de Oude Egyptenaren in de periode van 2000 tot 600 v.Chr. werkten met getallen.

Inhoud:

Inleiding

Zo'n 2000 jaar v.Chr., dus zo'n 4000 jaar geleden werd er in het Oude Egypte al volop gewerkt met getallen. Dat blijkt uit de zogenaamde Rhind-papyrus waarop de Egyptische schrijver Ahmes een groot aantal wiskundige problemen en hun oplossingen beschrijft. Deze problemen had hij verzameld uit de eeuwen voordat hij leefde (omstreeks 1650 v.Chr.). Andere (minder uitgebreide) bronnen van Oud-Egyptische wiskunde zijn de Moskou-papyrus, de Kahun-papyrus en de Berlijn-papyrus.
Daaruit blijkt dat de Egyptische samenleving in eeuwen van relatief stabiel bestuur een samenhangend systeem van getallen en rekenen met getallen wist op te bouwen. Dat dit gebeurde was ook niet zo vreemd: er ontstond voor het eerst een beschaving waarin van technologie sprake was, denk maar aan irrigatie en wegen, maar ook aan het bouwen van de piramiden. Bovendien waren de godsdienstige activiteiten sterk gebaseerd op de beweging van de zon en de maan en op het gedrag van de Nijl.

Schrijfwijze van getallen

De Oude Egyptenaren kenden symbolen voor 1, 10, 100, 1000, 10.000, 100.000 en 1.000.000. Met deze symbolen werden getallen gemaakt. Vaak schreven de Egyptenaren hun getallen van rechts naar links. In het oude hiëroglyfenschrift zag dat er zo uit:

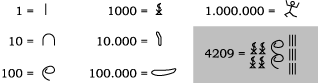
Bij een dergelijke schrijfwijze is de plaats van een symbool niet van belang: het Egyptische getalstelsel was geen positiestelsel zoals het onze. Ook een teken voor nul was daarom niet nodig. Het zou in feite nog vele eeuwen duren voordat zo'n symbool werd bedacht.

Optellen en aftrekken

Optellen is in het Oud-Egyptische getalstelsel heel eenvoudig: je gooit van beide getallen gewoon alle symbolen op één hoop. Daarbij worden 10 eenheden vervangen door één tiental, 10 tientallen door één honderdtal, etc. Kijk maar:

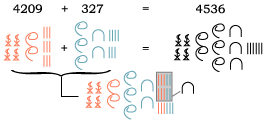
Als ze twee getallen van elkaar moesten aftrekken dan deden de Egyptenaren dat door het kleinste van de twee aan te vullen tot het grootste. Eigenlijk net zoals veel mensen uitrekenen hoeveel geld je terug krijgt als je € 7,84 betaalt met een briefje van € 10,00: het is nog 6 cent tot € 7,90, dan nog 10 cent tot € 8,00 en tenslotte nog 2 euro tot het tientje is bereikt, dus het verschil is € 2,16.
De uitkomst van 4209 − 327 vonden ze dus door 327 aan te vullen tot 4209 was bereikt. Bijvoorbeeld zo:

Zo vind je: 4209 − 327 = 3 + 70 + 600 + 3000 + 200 + 9 = 3000 + 800 + 70 + 12 = 3882.

Vermenigvuldigen en delen

De Oude Egyptenaren konden niet vermenigvuldigen zoals wij dat tegenwoordig doen: ze kenden immers ons tientallig stelsel niet. Ze werkten met verdubbelen en halveren en bij elkaar tellen. Hier zie je hoe dat gaat:

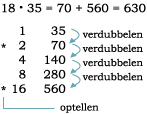
Wat in het Oud-Egyptische getalstelsel wel heel gemakkelijk gaat is het vermenigvuldigen met 10, of 100, of 1000, etc. Bijvoorbeeld bij vermenigvuldigen met 10 vervang je elk teken door het naast-hogere. Soms maakten ze ook daar gebruik van. Als een Egyptenaar bijvoorbeeld met vijf wilde vermenigvuldigen, dan kon hij dat doen door eerst het getal met 10 te vermenigvuldigen en dan door 2 te delen.

De vraag rijst natuurlijk of elke vermenigvuldiging is uit te voeren door verdubbelen, halveren en optellen. Dat blijkt inderdaad het geval te zijn, want elk natuurlijk getal is te schrijven als een som van machten van 2. (Dit is te bewijzen met de bewijsmethode van de volledige inductie, het dominoprincipe.)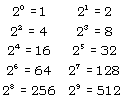
Om bijvoorbeeld 237 ⋅ 18 uit te rekenen, schrijf je eerst 237 als som van machten van 2. Je ziet:
237 = 128 + 109 = 128 + 64 + 45 = 128 + 64 + 32 + 13 = 128 + 64 + 32 + 8 + 5 =
= 128 + 64 + 32 + 8 + 4 + 1, dus
237 ⋅ 18 = (27 + 26 + 25 + 23 + 22 + 1) ⋅ 18
Dit betekent dat je 237 ⋅ 18 uitrekent door 18 zeven keer te verdubbelen en dan de zevende, de zesde, de vijfde, de derde, de tweede verdubbeling en 18 zelf bij elkaar op te tellen, uitkomst: 4266.

Bij delen werkten de Oude Egyptenaren op vergelijkbare wijze als bij aftrekken.
Stel je voor dat je 630 / 18 wilt uitrekenen.
In het Oude Egypte ging je dan met 18 aan het verdubbelen en optellen tot je op 630 uitkwam.

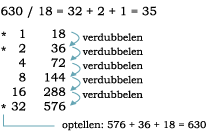
Bij delingen die 'uitkomen' (waarbij dus geen rest overblijft) werkt dit systeem prima. Maar hoe zit het met delingen die niet 'uitkomen'?

Breuken

Als een deling niet uit kwam (er bleef een ondeelbare rest over) werkten de Oude Egyptenaren met breuken. Alleen kenden zij geen breuken zoals wij, zij werkten vrijwel alleen met zogenaamde stambreuken. Stambreuken zijn breuken waarvan de teller 1 is, zoals 1/2, 1/3, 1/4, 1/5, etc.
De enige andere breuken die de Egyptenaren gebruikten waren 2/3 en 3/4.
Zij noteerden stambreuken door een 'open mond' boven de noemer te zetten. Voor enkele breuken bestonden speciale schrijfwijzen.

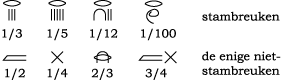
De wiskundige J.J. Sylvester (1814 - 1897) bewees vele eeuwen later dat elke breuk kan worden geschreven als de som van een aantal stambreuken. Hij ontwierp een eenvoudige manier waarmee elke breuk als som van stambreuken kan worden geschreven. Daarbij trek je telkens van de breuk die je wilt omzetten in een som van stambreuken een zo groot mogelijke stambreuk af. Bijvoorbeeld:
13/20 = 1/2 + 3/20 = 1/2 + 1/7 + 1/140.

Bij het delen (vooral bij delingen die niet 'uitkomen') gebruikten de Oude Egyptenaren verdubbelen en halveren. Hier zie je bijvoorbeeld (het is opgave 24 van de Rhind papyrus) hoe ze 19 deelden door 8:

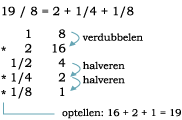
Je ziet dat de Egyptenaren vaak werkten met de rij 1/2, 1/4, 1/8, ...
Maar daarmee konden niet alle delingen worden gemaakt!
Daarom werden ook wel andere rijen gebruikt.
Bijvoorbeeld: 2/3, 1/3, 1/6, 1/12, ...
Deze rij ontstaat door eerst 2/3 deel te nemen en dan te halveren. Als je bijvoorbeeld 20/24 wilt uitrekenen is dit een goede aanpak.
Nog steeds kunnen niet alle delingen worden gemaakt. Er werden derhalve nog andere 'trucs' toegepast. Bijvoorbeeld:

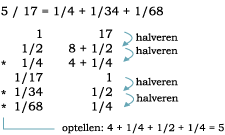
Hiermee is nog steeds niet alles gezegd over de Oud-Egyptische rekenkunde.
Er zijn delingen waarvoor nog weer andere technieken werden gebruikt. Bovendien waren de Egyptenaren in staat om breuken op elkaar te delen. Daarbij gebruikten ze tabellen, zoals een tabel waarin breuken van de vorm 2/m (met m oneven) werden geschreven als de som van stambreuken. (Als m een even getal is, is zo'n tabel overbodig, want dan is de breuk te vereenvoudigen tot de vorm 1/n.)
Lees verder in:

Toepassingen

De Oude Egyptenaren pasten hun rekenkundige kennis toe op zowel algebraïsche als meetkundige problemen. Je ziet er hier een paar voorbeelden van.

Eerst een hoeveelheidsberekening, het berekenen van een nog onbekende hoeveelheid. Tegenwoorig worden dergelijke problemen opgelost door voor de onbekende een letter te nemen en dan een vergelijking te maken.

Een hoeveelheid en het zevende deel van die hoeveelheid zijn samen 19. Hoe groot is die hoeveelheid?
Oplossing van de Oude Egyptenaren:
Neem aan dat de oplossing 7 is (eenzevende deel van 7 is gemakkelijk uit te rekenen).
Het totaal wordt dan 7 + 1/7 van 7, dus 8.
Nu is 19/8 = 2 + 2/3.
Dus is 19 te verdelen in 7 ⋅ (2 + 2/3) en 1 ⋅ (2 + 2/3).
De gezochte hoeveelheid is 7 ⋅ (2 + 2/3) = 16 + 5/8.

Het volgende voorbeeld is afkomstig van de Berlijnse papyrus. Het is een oppervlakteberekening met twee onbekenden.

De som van de oppervlakten van twee vierkanten is 100. Drie keer de zijde van het éne vierkant is even groot als vier keer de zijde van het andere vierkant. Hoe groot zijn de zijden van deze vierkanten?
Oplossing van de Oude Egyptenaren:
Neem aan dat de zijden 4 en 3 zijn.
De totale oppervlakte wordt dan 42 + 32 = 25.
Nu is 25 = 52 en 100 = 102.
Verder is 10/5 = 2.
De gezochte zijden zijn 2 ⋅ 4 = 8 en 2 ⋅ 3 = 6.

De meeste van de problemen die voorkomen op de eerder genoemde papyrussen lijken erg praktisch van aard. De wiskunde van de Oude Egyptenaren wordt dan ook vaak gezien als toegepaste rekenkunde. En die toepassingen waren ook vaak echt op de dagelijkse praktijk gericht zoals het verdelen van hoeveelheden, het bepalen van oppervlakte en inhoud, en dergelijke. Hoe dergelijke zaken moesten worden aangepakt werd uitgelegd in een groot aantal voorbeeldberekeningen. Vooral de Rhind-papyrus staat daar vol mee. De teruggevonden teksten moeten dan ook waarschijnlijk worden gezien als leerboeken voor mensen die dergelijke berekeningen moesten uitvoeren: beginnende rekenmeesters.