|
De oudst bekende systemen van getallen noteren en rekenen stammen uit het Oude Egypte en het Oude Mesopotamië. Hier wordt besproken hoe de Oude Mesopotamiërs in de periode van 2000 tot 600 v.Chr. werkten met getallen. Het oude Babylon was één van hun belangrijkste steden, daarom worden ze vaak Babyloniërs genoemd. Inhoud: |

Inleiding
Ongeveer 4000 jaar geleden leefden de Babyloniërs in Mesopotamië (het huidige Irak). Het schrift van de Babyloniërs is uitgevonden om handelsactiviteiten vast te leggen.
Bij de allereerste teksten die geschreven werden, zijn met een puntig voorwerp tekens in de vochtige klei getekend. Daarna legden de schrijvers de kleitablet in de zon om het schrift bestendig te maken. Al snel ontdekte men dat ze met een paar lijnen en punten hun teksten duidelijker weer konden geven.
Het was nodig om de tekens de standaardiseren zodat iedereen het kon begrijpen. Aangezien schrijvers niet langer probeerden een artiest te zijn, hoefde het instrument waarmee zij tekenden geen scherpe punt te hebben, maar kon het stomp of plat zijn. Bij het maken van tekens, raakte het uiteinde van een Stylus (een schrijfstift) als eerste de klei. Hierdoor gaf dit een bredere afdruk dan de afdruk van de schacht van de Stylus. De afdruk die nu gemaakt wat had de vorm van een spijker. Vandaar de naam "spijkerschrift".
Getallen
In alle soorten spijkerschrift komen getallen voor. In de oudste spijkerschriften, gedateerd uit 3000 voor Christus tot in de laatste uit 75 na Christus komen getallen voor. De Babyloniërs hadden een zestigtallig stelsel, ook wel sexagesimaal positiestelsel genoemd. Tegenwoordig wordt er nog steeds gebruikt gemaakt van het sexagesimale stelsel. Bijvoorbeeld bij minuten en seconden, maar ook bij hoeken die gemeten worden in graden en in de goniometrie.
Schrijfwijze van getallen
De Babyloniërs kenden maar twee symbolen, namelijk het symbool voor 1 en het symbool voor 10.
Het symbool voor 1 wordt ook gebruikt voor 60, 602, 603, enzovoort.
Ook wordt dit symbool gebruikt voor getallen als 1/60 1/602, 1/603, etc.
Het symbool voor 10 stelt 10 keer het symbool voor 1 voor.
De Babyloniërs maken geen gebruik van een komma en van het getal 0. Uit de context moet duidelijk worden welk getal bedoeld wordt. De Babyloniërs schrijven van links naar rechts, in het spijkerschrift zien de getallen van 1 t/m 59 er zo uit:
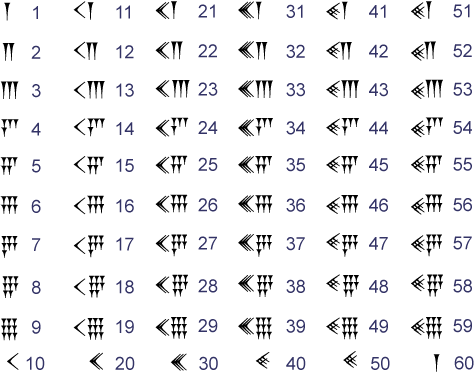
Het zestigtallige getallen stelsel van de Babyloniërs is een positiestelsel. Dat houdt in dat de plaats van een symbool van belang is voor de betekenis van het symbool. Ons eigen getallenstelsel is ook een positiestelsel, kijk maar:
8048 = (8 × 1000) + (0 × 100) + (4 × 10) + (8 × 1)
Bij het spijkerschrift gaat het precies hetzelfde:
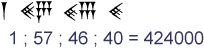
Als je bijvoorbeeld dit ontcijfert zie je dat er staat: (1 × 603) + (57 × 602) + (46 × 60) + 40 = 424000.
Het Babylonische spijkerschrift kan voor verwarring kan zorgen. Veel getallen kun je op meerdere manieren lezen. Kijk maar:
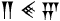
kan betekenen:
(2 × 60) + 40 + 5 =165
of (2 × 602) + (40 × 60) + 5 = 9605
of 2 + (45/60) = 2,75
Optellen en aftrekken
In het zestigtallige getallenstelsel van de Babyloniërs is optellen heel eenvoudig.
Je gooit van beide getallen gewoon alle symbolen op één hoop. De symbolen die daar uit komen worden dan vervangen door een vereenvoudigd symbool.
Hier zie je een voorbeeld:
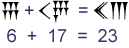
Bij aftrekken gaat het precies zo. Je trekt de ene hoop symbolen van de andere hoop af. Vervolgens vereenvoudig je de symbolen.
Vermenigvuldigen en delen
De Babyloniërs vermenigvuldigen op de zelfde manier als dat wij dat doen in ons huidige getallenstelsel. Hier zie je twee voorbeelden:
|
16 4 × ----- 24 40 + ----- 64 |
Dat is uitgewerkt: (4 × 6) + (4 × 40). De Babyloniërs doen dit op dezelfde wijze. Hieronder zie je de berekening in het spijkerschrift: 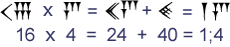 Merk op dat 1;4 = 64. |
|
64 53 × ----- 12 180 200 3000 + ------- 3392 |
Dat is uitgewerkt: (3 × 4) + (3 × 60) + (50 × 4) + (50 × 60). Hieronder zie je de berekening in het spijkerschrift: 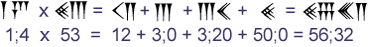 Merk op dat 56;32 = 3392. |
De Babyloniërs delen niet op de manier die wij nu gebruiken.
Om bijvoorbeeld 47/3 uit te rekenen, berekenen ze eerst de uitkomst van 1/3, en vermenigvuldigen dit vervolgens met 47.
Om deze berekeningen te maken gebruiken ze een delingstabel.
Omdat de Babyloniërs met een zestigtallig getallenstelsel werken en 1/2 hetzelfde is als 30/60,
geef je 1/2 weer als 0;30. De Babylonische delingstabel ziet er zo uit:
1/2 = 0;30
1/3 = 0;20
1/4 = 0;15
1/5 = 0;12
1/6 = 0;10
1/8 = 0;7;30
1/9 = 0;6;40
1/10 = 0;06
Hier zie je een voorbeeld van een deling:
30/3 = 0;20 × 30 = 0;600 = 10
Je kunt deze berekening ook in spijkerschrift noteren, kijk maar:
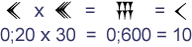
De stelling van Pythagoras
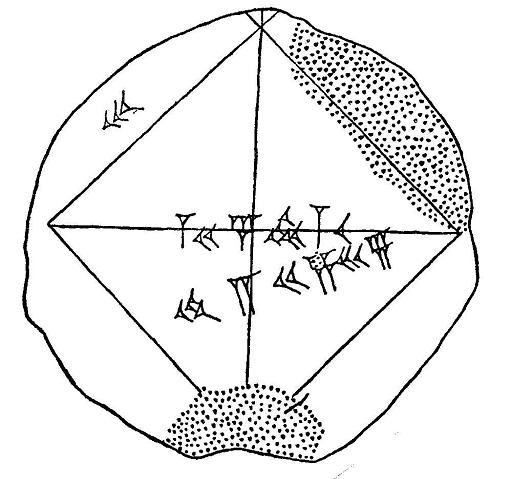
Er zijn veel kleitabletten van de Babyloniërs bewaard gebleven. Sommige van die kleitabletten laten ingewikkelde stukjes wiskunde zien. Een voorbeeld hiervan is de stelling van Pythagoras.
In deze figuur zie je een kleitablet van de Babyloniërs.
Om de diagonaal van een rechthoek te berekenen gebruik je wat wij tegenwoordig stelling van Pythagoras noemen, namelijk
a2 + b2 = c2
Ze zijn in de figuur uitgegaan van twee zijdes van 1.
De lengte van de diagonaal is een benadering van wortel 2.
Op de diagonaal van de figuur staat het getal 1,41421356...
Om aan dit getal te komen moet je de wortel van het getal 2 benaderen. Dit doen de Babyloniërs op de volgende manier: Je wilt een vierkant maken met een oppervlakte 2. Begin met een rechthoek met oppervlakte 2. Met een zijde van bijvoorbeeld 1,5 moet de andere zijde van 2 / 1,5 = 1,333... zijn. Van beide getallen neem je het gemiddelde, ongeveer 1.41667. Met dit getal reken je verder. Dit gebruik je nu als lengte van de éne zijde, de andere zijde is net zoals bij de eerste poging 2 / 1,41667. Het gemiddelde van deze twee getallen is 1.41422, etc.
Hoe vaker je deze berekening toepast op de getallen die er uit rollen, hoe dichter je bij de uitkomst van wortel 2 komt.
Het verschil met onze decimale schrijfwijze van wortel 2 (1,414296) is kleiner dan een miljoenste!
Links boven staat het getal 30. Onder de notatie van wortel 2 staat 42,426389. Dat is precies 30 keer de diagonaal bij twee zijdes van 1.
Dit kleitablet geeft de lengte van de diagonaal en van de zijde aan en hun onderlinge verhoudingen.
Wat met dit tablet ook blijkt, is dat de stelling van Pythagoras 1200 jaar ouder moet zijn dan de tijd waarin Pythagoras leefde. Pythagoras leefde immers ongeveer 500 jaar voor Christus.
![]() Math4all
Math4all
Dit artikel is geschreven door Michelle van Os en Lieke Huisman, twee A6-leerlingen van de Koninklijke Scholengemeenschap in Apeldoorn. Ze hebben deze tekst gemaakt in 2006/2007 in het kader van hun profielwerkstuk voor het vak wiskunde A1,2.


