| Karl Weierstrass (1815 - 1897) kwam pas na zijn veertigste jaar terecht in de beroepswereld waar hij thuishoorde, de wereld van het wiskundig onderzoek aan een universiteit. Tot die tijd was hij wiskundig wel actief, maar in de wiskundewereld vrijwel onzichtbaar geweest. Daarna rees zijn ster snel en ontwikkelde hij zich tot de belangrijkste wiskundige in Berlijn. Hij is vooral bekend om zijn werk over complexe functies en om zijn streven naar wiskundige precisie. Hij wordt wel de kampioen van de precisie genoemd. De oorsprong van zijn opmerkelijk verlopen loopbaan is misschien terug te voeren op zijn vader die hem van een wiskundestudie afhield en zijn zoon liever het pad van rechten en economie opstuurde om, net als hij zelf, in de ambtenarij op te klimmen.
» De tijd van Weierstrass
|
 |
|
Links naar ander(stalig)e sites: » Over Weierstrass |
De tijd van Weierstrass
Weierstrass wordt geboren in de periode dat Napoleons rol definitief ten einde is. Tijdens het congres van Wenen (1814-1815) komt een nieuwe indeling van diverse landen tot stand. Er ontstaat geen verenigd Duitsland, maar een los samenwerkingsverband in de vorm van een bond van 37 zelfstandige Duitse staten, waarin Pruisen en aanvankelijk ook Oostenrijk een dominante rol spelen.
Voor wat deze Duitse staten betreft, staat de rest van de 19e eeuw in grote lijnen in het teken van de eenwording van de statenbond tot uiteindelijk een Duits keizerrijk. Revoluties in Frankrijk in 1830 in 1848 stimuleerden ook in de Duitse staten een toenemende invloed van burgers en een vanuit het volk gedragen wens tot eenwording. In 1848 lijkt het zo ver als een revolutie in Frankrijk overslaat naar onder meer Berlijn.

Deze ontwikkeling wordt echter in de kiem gesmoord.
Naar aanleiding van onenigheid over het bestuur van de door Oostenrijk en Pruisen bij de Duitse Bond ingelijfde Deense delen in de jaren 1860, splitst de Duitse Bond in een Noordduitse Bond onder leiding van Pruisen en een Zuidduitse Bond die de Pruisische ministerpresident Bismarck echter steeds meer naar zich toe trok via handelsverdragen. De overwinning in de Frans-Duitse oorlog van 1870-1871 waarin de Zuidduitse staten aan Pruisische zijde streden, maakt de positie van Pruisen zo sterk dat Bismarck kans ziet de Duitse bonden op te laten gaan in een Duits keizerrijk met de Pruisische koning Wilhelm I als keizer en hem zelf als rijkskanselier.

Het leven van Weierstrass
Karl Weierstrass werd in 1815 geboren te Ostenfelde in de buurt van Münster (Duitsland) als oudste van vier kinderen van Wilhelm Weierstrass, toen de secretaris van de burgemeester, en Theodora von der Forst. Karls moeder overleed kort na de geboorte van zijn jongste zusje Elise en zijn vader hertrouwde enkele jaren later. Zijn middelbare schooltijd bracht hij door in Münster en later in Paderborn, de plaats waar zijn vader aan een nieuwe baan was begonnen. Hij deed het goed op school, won diverse prijzen en verdiepte zich al in het "Zeitschrift für die reine und angewandte Mathematik" dat op zijn school aanwezig was. Toen moet hij zijn voorliefde voor de wiskunde ontdekt hebben. Maar zijn vader had iets anders met hem voor dan wiskunde studeren: het werd een studie rechten, financiën en economie in Bonn ("Kameralwissenschaft"). Na vier jaar had Karl nog geen diploma: hij had zich meer in het studentenleven gestort, was een prima schermer geworden en had zeer waarschijnlijk op eigen houtje de nodige wiskunde doorgewerkt en wiskundecolleges bezocht.
Een uitweg uit deze pijnlijke situatie werd gevonden door in Münster een onderwijsbevoegdheid te halen. Daar volgde hij (als enige!) een cursus elliptische functies bij Christoff Gudermann. Het boeide Karl zo dat hij zich voor het examen extra diep in een wiskundig probleem op dat gebied wilde verdiepen, ook al was dat niet vereist. Gudermann was zo onder de indruk van het resultaat dat hij graag zag dat Karl een baan aan een universiteit zou krijgen. Maar met zijn diploma was hij alleen maar bevoegd les te geven op een middelbare school. Er volgden jaren van lesgeven op diverse scholen, niet alleen in wiskunde, maar ook in natuurkunde en zelfs in Duits, geschiedenis, aardrijkskunde, gymnastiek en schoonschrijven!
Als hij tijd vrij had dook hij in de wiskunde, vaak ook 's nachts. Een ochtend, zo gaat het verhaal, was hij niet komen opdagen voor de lessen en werd hij in zijn kamer aangetroffen met gesloten gordijnen. Hij had de hele nacht doorgewerkt en niet eens in de gaten gehad dat het al weer licht geworden was. Hij kon onmogelijk les komen geven, omdat hij op het punt stond iets belangrijks te ontdekken! De resultaten van zijn onderzoek publiceerde hij in schoolkranten, niet bepaald een manier om de wiskundewereld te bereiken. Een artikel over abelse functies publiceerde hij tenslotte wel in een wiskundig vaktijdschrift, en niet zonder gevolgen: toen het in 1854 verscheen was Weierstrass op slag bekend in de wiskundewereld. Hij kreeg een eredoctoraat van de universiteit van Königsberg en zijn wetenschappelijke loopbaan kreeg vaart: een baan aan de universiteit in Berlijn en een professoraat aan wat later de Technische Universität Berlin zou worden.
Mede dankzij Weierstrass groeide de universiteit van Berlijn op wiskundig gebied naar de wereldtop in de tweede helft van de 19e eeuw. Legendarisch waren zijn colleges, die niet alleen in Duitsland bekend waren, maar ook ver daarbuiten. Hij gaf zijn onderwijs steeds in vier collegereeksen:
- Inleiding in de analytische functies,
- Elliptische functies,
- Abelse functies,
- Variatierekening.
Via zijn colleges werden diverse nieuwe ideeën van Weierstrass verspreid. Zelf nam hij niet altijd de moeite zijn resultaten te publiceren. Diverse leerlingen pikten zijn ideeën op en zorgden voor de verspreiding ervan. Een van die leerlingen was de Russische Sofia Kovalevskaya, die als vrouw niet toegelaten werd tot de universiteit van Berlijn, maar mede dankzij privélessen van Weierstrass toch kon uitgroeien tot de eerste vooraanstaande vrouwelijke wiskundige in de moderne tijd.

Weierstrass' belangrijkste werk
Reeksen
Weierstrass werkte voornamelijk aan functies. Hij zocht onder meer naar manieren om functies te beschrijven met behulp van zogenaamde convergente reeksen, dat wil zeggen als oneindige som van, liefst eenvoudige, uitdrukkingen. Zo kun je de functie voorstellen als de oneindige som
voor waarden van
die inliggen tussen
en
(een zogenaamde meetkundige reeks).
Een opvallend fenomeen is het verschijnsel dat sommige reeksen van continue functies geen continue som opleveren (zie hieronder voor het begrip continuïteit). Cauchy had hier een subtiel punt over het hoofd gezien, dat door Dirichlet en Riemann al was geconstateerd.
Het was Weierstrass die het begrip convergentie verfijnde tot zogenaamde uniforme convergentie.
Reeksen van continue functies die aan deze strengere voorwaarde voldoen, hebben een som die gegarandeerd continu is. Weierstrass leidde ook een stelling af die vaak gebruikt kan worden om vast te stellen dat een reeks van functies uniform convergeert zonder de definitie van uniforme convergentie na te hoeven lopen, de zogenaamde Weierstrass M-test.
Je kunt concluderen dat een reeks van functies op een interval uniform convergeert als het volgende het geval is:
als er een rij positieve getallen
bestaat zo, dat de oneindige som
bestaat (een gewoon getal is), en
,
,
enz. voor alle
uit het interval, dan is de reeks
uniform convergent.
Met deze test volgt uit de ongelijkheid
voor
en het feit dat
gelijk is aan
dat de oneindige som
een continue functie voorstelt.
Continuïteit: een wiskundig preciese definitie
Een continue functie op een interval is, eenvoudig gezegd, een functie waarvan je de grafiek kunt tekenen zonder je pen van het papier te halen. Onder invloed van Weierstrass vond een degelijke definitie van het begrip continue functie algemeen ingang. In die definitie staan geen vaagheden meer over 'oneindig kleine' getallen en dergelijke zoals voor de 19e eeuw het geval was.
De prijs is wel dat het best wat moeite kost de definitie te doorgronden.
Hier is de definitie van 'de functie
, gedefinieerd op een interval dat
bevat, is continu in
.
|
De functie
is continu te
als het volgende geldt: voor elk getal groter dan , moet er een getal aan te geven zijn, ook groter dan , zodat het volgende waar is: als dan is . |
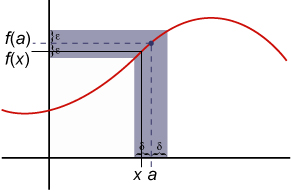
(Het laatste deel in woorden: als de afstand tussen
en
kleiner is dan
dan is de afstand tussen
en
gegarandeerd kleiner dan
.)
Nog iets anders gezegd:
Met de preciese definitie van continuïteit in een punt kun je bijvoorbeeld bewijzen dat de volgende functie niet continu is in
:
de functie
voor alle reële getallen gedefinieerd door
als
en
als
of
.
Als je namelijk in de definitie van continuïteit voor ε bijvoorbeeld de waarde
kiest (elk positief getal kleiner dan
werkt voor dit argument), dan kun je geen enkele geschikte
vinden.
Welke positieve
je namelijk ook kiest,
en dat is groter dan de gekozen
.
Ook op dit terrein is het werk van Weierstrass vaak indirect in de wiskundewereld verspreid. Zo publiceerde Eduard Heine (1821 - 1881) een definitie van een verscherping van het begrip continuïteit, zogenaamde uniforme continuïteit, die van Weierstrass afkomstig is en zeer nuttig is gebleken.
Continue functies die in geen enkel punt een afgeleide hebben
Tot ver in de 19e eeuw dacht men dat alle continue functies voor elke waarde een afgeleide hebben (differentieerbaar zijn), misschien met uitzondering van een beperkt aantal. Des te groter was de verrassing dat er continue functies bestaan die in geen enkele waarde een afgeleide hebben! Vertrouwd als hij was met reeksen, beschreef Weierstrass in de jaren 1860 zo'n functie, in de vorm van een reeks. Voor elk oneven getal en een reëel getal dat in het interval ligt, terwijl groter dan is, definieert de som
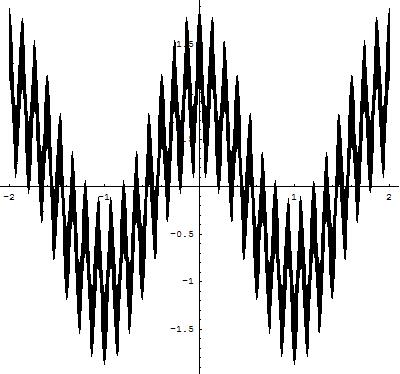
een continue functie die in geen enkel punt differentieerbaar is.
Je kunt bijvoorbeeld
en
nemen.
De figuur hiernaast is voor dit geval een benadering van
.
Om in te zien dat de somfunctie continu is, kun je Weierstrass' M-test gebruiken!
Omdat
,
,
enz.,
en
eindig is (meetkundige reeks) volgt uit de Weierstrass M-test dat
een continue functie is (zie boven).
Dat
in geen enkele waarde een afgeleide heeft vergt een diepergaande analyse die we hier achterwege laten.
Zoals wel vaker bij Weierstrass publiceerde hij het resultaat niet zelf. In 1875 verscheen dit resultaat in druk in een publicatie van Paul du Bois-Reymond.




