Je krijgt dan in je rekenscherm: QuadReg L1, L2
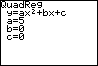 Als je nu op [ENTER] drukt, vind je de formule met de juiste waarden voor a, b en c onder elkaar
Als je nu op [ENTER] drukt, vind je de formule met de juiste waarden voor a, b en c onder elkaar Inhoud
| tijd (in seconden) | 0 | 1 | 2 | 3 | 4 |
| afstand (in m) | 0 | 5 | 20 | 45 | 80 |
Deze tabel kun je in je grafische rekenmachine invoeren in lijsten met getallen, L1 en L2. Voer daartoe in je rekenscherm in:
Eerst bedenk je welke soort formule je wilt gebruiken. Vaak heb je daar wel informatie over, bijvoorbeeld je zoekt naar exponentiële groei, of naar een lineair verband.
Bij deze tabel hoort een kwadratisch verband. De bijbehorende formule vind je nu door in te toetsen:
 Als je nu op [ENTER] drukt, vind je de formule met de juiste waarden voor a, b en c onder elkaar
Als je nu op [ENTER] drukt, vind je de formule met de juiste waarden voor a, b en c onder elkaar
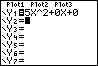 Ga na, dat bij de tabel hierboven de formule y = 5x2 past. Controleer ook de tabel met de tabel die hierboven is gegeven.
Ga na, dat bij de tabel hierboven de formule y = 5x2 past. Controleer ook de tabel met de tabel die hierboven is gegeven.
Zoek nu zelf een tabel waarin sprake is van een lineair verband en maak daarbij een formule. Doe hetzelfde met een tabel voor exponentiŽle groei.
| tijd (in seconden) | 0 | 1 | 2 | 3 | 4 |
| afstand (in m) | 0 | 5,1 | 19,6 | 44,9 | 80,1 |
Bij deze tabel past niet precies één van de genoemde verbanden. Maar toch lijkt hij zoveel op de vorige tabel, dat je veilig weer kunt uitgaan van een kwadratisch verband.
Voer opnieuw deze tabel in twee lijsten in (L1 en L3). Zoek weer een kwadratische formule en zorg er voor dat die kwadratische formule in het Y= scherm terecht komt als Y2. Je ziet dat je rekenmachine de opdracht keurig uitvoert, alleen komen er voor a, b en c erg veel decimalen in beeld. Op één decimaal nauwkeurig vind je:
y = 5,1x2 – 0,3x + 0,1
Als je nu de tabel van deze formule vergelijkt met de hierboven gegeven tabel, zie je (kleine) afwijkingen. In één decimaal nauwkeurig:
| tijd (in seconden) | 0 | 1 | 2 | 3 | 4 |
| afstand (in m) | 0,1 | 4,9 | 19,8 | 44,9 | 80,1 |
Als in een bepaalde situatie de afwijkingen te groot zijn is je model niet goed. Misschien bestaat er dan wel geen formule van de vorm die jij hebt gekozen bij de gegeven tabel. Zoek dan bijvoorbeeld naar een andere soort formule.
Je grafische rekenmachine kent ook een maat voor de betrouwbaarheid jouw formule. Daarover vind je meer in de handleiding. Dat valt buiten het bestek van dit practicum.