Basistechnieken TI-83/84

Als je dit practicum doorwerkt, weet je de eerste beginselen van het werken met de grafische rekenmachine TI-83 of de TI-84. De TI-83/84 Plus werkt vrijwel net zo. In de tekst van het practicum wordt zo aangegeven dat je op een toets moet drukken: [toets].

Inhoud

Aanzetten
Rekenen
Grafieken maken
Vergelijkingen oplossen met de 'Solver'
Snijpunten van twee grafieken

De TI-83 aanzetten

Je zet de machine aan door [ON] in te drukken. De betreffende knop zit links onderaan! Door middel van [2nd][ON] kun je de machine weer uit zetten.

Je ziet nu het scherm oplichten met een knipperende cursor (een blokje) in beeld, of je ziet nog werk van de vorige gebruiker. Zie je (vrijwel) niets, dan moet je het scherm helderder maken door [2nd] te toetsen en daarna de pijltjestoets naar boven [^] even vast te houden. (Als dat allemaal niet helpt, raadpleeg dan je leraar!)

De knop [CLEAR] veegt het hoofdscherm schoon, of brengt je naar dit hoofdscherm terug.

Je kunt eenvoudig alle eventueel aanwezige programma's en gegevens wissen:

[2nd] [ + ] geeft het MEM menu (memory = geheugen);
kies 5: Reset en dan 1: All Memory en tenslotte 2: Yes.
(TI-83Plus: 7: Reset en dan 1: All RAM)

Soms moet je daarna meteen het scherm weer helderder maken omdat ook de helderheidsinstelling weer terugvalt naar de standaardinstelling.

De knop [2nd] activeert de 'gele functie' van een toets.
Bijvoorbeeld: [2nd] [ ^ ] geeft een benadering van het getal pi.
De knop [ALPHA] activeert de 'groene functie' van een toets.
Bijvoorbeeld: [ALPHA] 1 geeft de letter: Y.
Zo kun je je naam schrijven...

Rekenen

In grote lijnen werkt de TI-83 net zoals de rekenmachine die je tot nu toe gebruikt hebt, alleen zijn er waarschijnlijk verschillen in de manier van invoeren van de berekening.

Bijvoorbeeld de wortel van 25 bereken je zo:

[2nd] [ x² ] 25 [ ) ] [ENTER]

Je ziet dat het scherm van de TI-83 een soort kladblok is: je schrijft de berekening gewoon op en met [ENTER] wordt hij uitgevoerd. Het haakjes sluiten is hier niet beslist noodzakelijk, maar wel als je de wortel van (16 + 9) wilt berekenen! Probeer maar...

[(–)] is de toets waarmee je van teken wisselt (en dus een negatief getal invoert).

Bij berekeningen met sin, cos en tan, moet je erom denken dat je (voorlopig) in graden moet werken. Je kunt dat instellen door op [MODE] te drukken. Je ziet dan een keuzemenu waar je met behulp van de pijltjestoetsen doorheen kunt lopen. Loop naar 'Degree' en toets [ENTER]. Met [CLEAR] kom je weer in het hoofdscherm. Je kunt nu sin 30° berekenen door in te toetsen: [SIN] 30 [ENTER].
Antwoord: 0.5.

Terugrekenen kan zo: [2nd] [SIN] [2nd] [(–)] [ENTER].
Antwoord: 30.
Met [2nd] [ (-) ] gebruik je ANS (answer), dus het antwoord van de vorige berekening.

Voor sommige wiskundige (mathematische) berekeningen is er de knop [MATH]. Als je die intoetst krijg je vier menu's. Je loopt er weer met de pijltjestoetsen doorheen. Je vindt er een aantal keuzemogelijkheden voor wiskundige berekeningen. Met [CLEAR] keer je weer terug naar het hoofdscherm.

Als je een opgave fout hebt ingevoerd en daarna berekend, kun je die opgave met behulp van ENTRY nog eens in je scherm krijgen. Je toetst daartoe: [2nd] [ENTER].
Je kunt vervolgens met de pijltjestoetsen door die opgave lopen.
Verbeteren kun je hem door:

over een verkeerd teken het juiste teken te typen;
met [DEL] en [2nd] [DEL] (insert is invoegen) tekens weg te halen en/of toe te voegen.

Rekenvoorbeelden

Opgave Intoetsen Uitkomst

0,625 schrijven als breuk .625 [MATH] kies 1: >Frac en toets [ENTER] 5/8

6² berekenen 6 [ x² ] en [ENTER] 36

de wortel van 36 met 0,1 vermenigvuldigen [2nd] [ x² ] 36 [ ) ] [ × ] .1 en [ENTER] (Denk aan het sluithaakje!) .6

6³ berekenen 6 [ ^ ] 3 en [ENTER]
of: 25 [MATH] en met pijltjestoets naar 3 en [ENTER] [ENTER] 216

de derdemachtswortel uit 50 berekenen [MATH] en naar 4 [ENTER] 50 [ ) ] [ENTER] 3.684031499

6 delen door 2³ – 5;
bereken dus: 6 2 3 −5 6 [ ÷ ] [ ( ] 2 [ ^ ] 3 [ - ] 5 [ ) ] en [ENTER] 2

bereken:
2,6 × 10⁶ × –1,14 × 10^–5 eerste manier:
2.6 [ × ] 10 [ ^ ] 6 [ × ] [ (–) ] 1.14 [ × ] 10 [ ^ ] [ (–) ] 5 en [ENTER]
tweede manier (met EE):
2.6 [2nd] [ , ] 6 [ × ] [ (–) ] 1.14 [2nd] [ , ] [ (–) ] 5 en [ENTER] –29.64

Zelf even narekenen:

(–4)³ + 6² = –28

3 6 + 30 3 ≈ 10,45570173

4 3 π · 12³ ≈ 7238,229474

−5+ 5 2 −4⋅0,5⋅3 2⋅0,5 ≈ –0,6411010565

−5− 5 2 −4⋅0,5⋅3 2⋅0,5 ≈ –9,358898944

–1,42 · 10⁶ + 0,92 · 10⁷ = 7780000

6 5 7 – 4 7 8 = 103 56

5−12 8−1 = –1

Grafieken maken

Hét sterke punt van de grafische rekenmachine is het tekenen van grafieken bij een ingevoerde formule. Als je de machine in de MODE: Function zet, kan hij grafieken tekenen bij formules van de vorm Y = ...
Toets [MODE] en loop met de pijltjestoetsen naar Func. Vervolgens [ENTER] en [CLEAR].

Je gebruikt voor grafieken vooral de toetsen die direct onder het beeldscherm zitten.

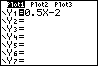Zo kun je bijvoorbeeld een grafiek tekenen bij de formule:
y = 0,5x - 2.

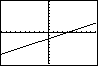toets [ Y= ] en je krijgt nu een lijst te zien waarin formules van de vorm y = ... kunnen worden ingevoerd: Y1, Y2, ..., Y0 (Met de pijltjestoetsen kun je door deze lijst lopen. Met [CLEAR] haal je al ingevulde formules weg);
plaats de cursor achter Y1= en toets 0.5 [X,T,q,n] [ – ] 2; je hebt nu de formule ingevoerd;
toets daarna: [GRAPH]; in principe krijg je nu de grafiek in beeld (Dat hoeft echter niet, want het kan zijn dat de grafiek buiten het schermgebied ligt. Toets dan [ZOOM] en kies met behulp van de pijltjestoetsen ZStandard [ENTER]. De grafiek is nu normaal gesproken te zien).

Toets [WINDOW] en je krijgt de vensterinstellingen te zien. Dus tussen welke waarden de variabele x (van Xmin tot Xmax) loopt en tussen welke waarden de variabele y (van Ymin tot Ymax) loopt. 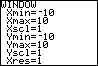Met de pijltjestoetsen kun je door de lijst gaan en getallen veranderen. Door [GRAPH] te toetsen krijg je steeds verschillende delen van de grafiek in beeld.
Xscl en Yscl leggen de eenheid (scale = schaal) op de assen vast. Experimenteer er maar even mee...

Toets [TRACE] en je ziet een aantal dingen in je scherm verschijnen: een knipperende cursor op de grafiek bij je formule; de x-coördinaat en de y-coördinaat van die cursor; links boven in het scherm de formule die bij de grafiek van Y1 hoort. Met de pijltjestoetsen kun je nu de cursor over de grafiek verplaatsen en de bijbehorende coördinaten aflezen. Heb je meerdere grafieken, dan kun je met de pijltjestoetsen (omhoog en omlaag) ook van de éne naar de andere springen. 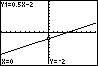De cursor doorloopt de grafiek in sprongen. Het nulpunt (het punt met y = 0) is dus niet nauwkeurig te vinden met de TRACE-routine. Probeer maar...

Als je de coördinaten van zo'n nulpunt nauwkeuriger wilt vaststellen, moet je de grafiek vergroten: je moet dan inzoomen op de grafiek. Toets [ZOOM] en kies ZBOX [ENTER]. Je kunt dan met behulp van de pijltjestoetsen een rechthoekje om het gewenste punt tekenen: kies eerst met de cursor een punt bijvoorbeeld links onder het gewenste punt, toets [ENTER] en gebruik dan een pijltjestoets om het rechthoekje in te stellen, toets weer [ENTER] en het rechthoekje ligt vast en de grafiek komt vergroot in beeld. Met [TRACE] kun je nu het nulpunt nauwkeuriger bepalen.

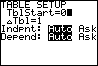
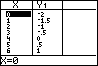Toets [2nd] [GRAPH] en je krijgt via de TABLE-routine een tabel bij de grafiek te zien: een lijst met x-waarden en de bijbehorende y-waarden waar je met de pijltjestoetsen doorheen kunt lopen. De stapgrootte in de tabel kun je veranderen met TblSet, zoek maar even.

Tenslotte nog dit:
Je kunt het beeldscherm van de TI-83 splitsen. Als je bij [MODE] kiest voor Full (standaard ingesteld), dan krijg je een volledig scherm. Met de keuze Horiz wordt het scherm horizontaal gesplitst als je [GRAPH] toetst en kun je in de onderste helft het Y= scherm, of het WINDOW-scherm oproepen. Met de keuze G-T zie je de tabel naast de grafiek verschijnen als je [GRAPH] toetst.

Oefenen

Teken grafieken bij de volgende formules. Kies de beste beelscherminstellingen om de grafieken in beeld te brengen. Zoek snijpunten met de assen en onderlinge snijpunten op, maak een tabel bij elke formule.

y = –0,5x² + 8
y = 20 – x
y = 10x²(x – 10)
y = x⁴ – 16

Experimenteer vervolgens een tijdje met iemand samen: geef elkaar verschillende formules op die de ander dan zo mooi mogelijk in beeld moet brengen. Laat elkaar snijpunten met de assen, onderlinge snijpunten en dergelijke opzoeken.

Vergelijkingen oplossen met de 'Solver'

Met de TI-83 kun je op diverse manieren vergelijkingen oplossen. Een heel rechtstreekse manier is het gebruiken van de 'Solver' (= oplosser). Andere manieren hebben vaak met grafieken te maken. Daarover meer in het practicum: Functies.

Zo kun je deze vergelijking oplossen:
0,5x - 2 = 12

schrijf de vergelijking eerst in de vorm: 0 = ...;
hier: 0 = 0,5x - 14
roep vervolgens via [MATH] 0: Solver... [ENTER] de solver op in het rekenscherm;
er zijn nu twee mogelijkheden:
- je krijgt het scherm hiernaast te zien: tik dan achter 0 = de vergelijking 0,5 [ALPHA] [STO>] [ - ] 14 en [ENTER] (Met [ALPHA] [STO>] krijg je de letter X, maar dat kan ook via [X,T,q,n]. Je kunt echter ook andere (meerdere) letters in de SOLVE-routine gebruiken.);
- er staat nog een vorige vergelijking in het scherm, zodat je meteen die vergelijking krijgt te zien en de cursor op X=0 knippert: ga dan met de pijltjestoets naar boven naar het scherm hierboven en voer de hierboven beschreven stappen uit;
je hebt nu de vergelijking in beeld en de cursor knippert achter X=; dat betekent dat de TI-83 een waarde voor X gaat zoeken, te beginnen bij X=0 (bound={-1E99,1...} betekent dat hij zoekt op het hele gebied dat de TI-83 bestrijkt, je kunt dit zoekgebied kleiner maken, als je weet welk antwoord er ongeveer uit zal komen);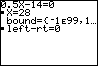
toets [ALPHA] [ENTER] en je krijgt het antwoord: X=28.
De uitdrukking: left-rt=0 betekent dat de oplossing exact is gevonden (Het verschil tussen de benadering en de oplossing is 0).

Met enige oefening zal de 'Solver' je goede diensten kunnen bewijzen. Er zijn echter wel een paar haken en ogen:

Je krijgt zo maar één oplossing, terwijl vergelijkingen wel meerdere oplossingen kunnen hebben.
Bij een vergelijking met meerdere oplossingen krijg je misschien niet de oplossing die voor jouw probleem nodig is.

Deze problemen kun je oplossen door het juiste zoekgebied in te stellen (achter bound=). Let er dan wel op dat de startwaarde dan ook binnen dit zoekgebied moet vallen!

Oefenen

Los de volgende vergelijkingen volledig op (d.w.z. dat je alle oplossingen moet vinden):

Opgave Uitkomst

a 0,05x + 50 = 0,25x + 20 x = 150

b x² – 4x = 12 x = 6 of x = –2

c 8x – x³ = 0 x = 0 of x = 2,857142857... of x = –2,857142857...

d 210x^1,23 = 400 x = 1,688545476...

Oefen het oplossen van vergelijkingen met iemand anders samen.

Snijpunten van twee grafieken

Voor het bepalen van de snijpunten van de grafieken van twee functies kun je TABLE of TRACE gebruiken. Dit gaat echter sneller met het CALC-menu.

Gebruik de formules

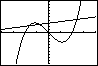
y₁ = x³ – 4x en y₂ = 0,5x + 3

Breng beide grafieken netjes in beeld, kies zodanige vensterinstellingen dat x loopt vanaf –4 t/m 4 en y loopt vanaf –10 t/m 10. Je krijgt de drie snijpunten keurig in beeld. Met TRACE of met TABLE kun je ze wellicht vinden.
Met CALC gaat dat zo:

Kies in het CALC-menu 5: intersect [ENTER].
Je moet nu in de buurt van het gewenste snijpunt gaan staan met de cursor.
De rekenmachine vraagt of dit één van de twee grafieken is (First curve ?). Als dat niet zo is (er kunnen nog wel veel meer grafieken in je scherm staan dan die van y₁ en y₂, dan ga je met de pijltjestoetsen (omhoog en/of omlaag) naar een gewenste grafiek en [ENTER]. Als dat wel zo is, toets je meteen [ENTER].
De rekenmachine vraagt of dit de andere grafiek is (Second curve ?). Als dat zo is, doe je weer [ENTER].
Vervolgens vraagt de rekenmachine of zijn gok (Guess?) juist is. Nu kun je in de buurt van het gewenste snijpunt gaan staan en [ENTER].
Nu wordt het dichtstbijzijnde snijpunt van y₁ en y₂ berekend.

Bereken de snijpunten van de grafieken van f en g. Als het goed is vind je (in drie decimalen nauwkeurig):
(–1,631; 2,184), (–0,767; 2,617) en (2,398; 4,199).

Math4all

Opgave	Intoetsen	Uitkomst
0,625 schrijven als breuk	.625 [MATH] kies 1: >Frac en toets [ENTER]	5/8
6² berekenen	6 [ x² ] en [ENTER]	36
de wortel van 36 met 0,1 vermenigvuldigen	[2nd] [ x² ] 36 [ ) ] [ × ] .1 en [ENTER] (Denk aan het sluithaakje!)	.6
6³ berekenen	6 [ ^ ] 3 en [ENTER] of: 25 [MATH] en met pijltjestoets naar 3 en [ENTER] [ENTER]	216
de derdemachtswortel uit 50 berekenen	[MATH] en naar 4 [ENTER] 50 [ ) ] [ENTER]	3.684031499
6 delen door 2³ – 5; bereken dus: 6 2 3 −5	6 [ ÷ ] [ ( ] 2 [ ^ ] 3 [ - ] 5 [ ) ] en [ENTER]	2
bereken: 2,6 × 10⁶ × –1,14 × 10^–5	eerste manier: 2.6 [ × ] 10 [ ^ ] 6 [ × ] [ (–) ] 1.14 [ × ] 10 [ ^ ] [ (–) ] 5 en [ENTER] tweede manier (met EE): 2.6 [2nd] [ , ] 6 [ × ] [ (–) ] 1.14 [2nd] [ , ] [ (–) ] 5 en [ENTER]	–29.64

Opgave		Uitkomst
a	0,05x + 50 = 0,25x + 20	x = 150
b	x² – 4x = 12	x = 6 of x = –2
c	8x – x³ = 0	x = 0 of x = 2,857142857... of x = –2,857142857...
d	210x^1,23 = 400	x = 1,688545476...