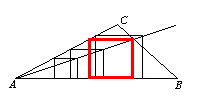
Maak eerst een tekening van een driehoek. De lange zijde is voor het gemak horizontaal getekend. Nu lijkt proberen de aangewezen weg. Teken er maar eens een paar vierkantjes in.
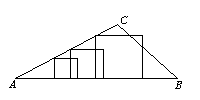 Zorg er voor dat in ieder geval aan een deel van de voorwaarden is voldaan: één zijde op de lange zijde van de driehoek en in ieder geval één hoekpunt op één van de korte zijden. Hier zie je een paar probeersels.
Nu moet je proberen te ontdekken of je aan al die probeersels iets herkent. Of ze allemaal eenzelfde eigenschap hebben waar je gebruik van kunt maken. Gemakkelijk is dat niet, probeer eventueel meer vierkantjes. Het lijkt er op dat alle "losse hoekpunten" (de hoekpunten die nog niet op een zijde van de driehoek liggen) recht achter elkaar liggen, dus op een rechte lijn liggen. Die rechte lijn moet dan wel door A gaan (waarom?).
Zorg er voor dat in ieder geval aan een deel van de voorwaarden is voldaan: één zijde op de lange zijde van de driehoek en in ieder geval één hoekpunt op één van de korte zijden. Hier zie je een paar probeersels.
Nu moet je proberen te ontdekken of je aan al die probeersels iets herkent. Of ze allemaal eenzelfde eigenschap hebben waar je gebruik van kunt maken. Gemakkelijk is dat niet, probeer eventueel meer vierkantjes. Het lijkt er op dat alle "losse hoekpunten" (de hoekpunten die nog niet op een zijde van de driehoek liggen) recht achter elkaar liggen, dus op een rechte lijn liggen. Die rechte lijn moet dan wel door A gaan (waarom?).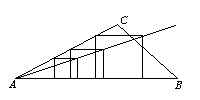 Nu je dit hebt ontdekt is de oplossing niet meer ver weg.
De getekende rechte lijn snijdt immers de korte zijde van de driehoek waar nog geen hoekpunt van het vierkant op ligt. Dit belangrijke punt zie je in de volgende tekening. Vanuit dat punt kun je het bedoelde vierkant tekenen.
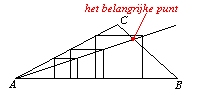
Nu je dit hebt ontdekt is de oplossing niet meer ver weg.
De getekende rechte lijn snijdt immers de korte zijde van de driehoek waar nog geen hoekpunt van het vierkant op ligt. Dit belangrijke punt zie je in de volgende tekening. Vanuit dat punt kun je het bedoelde vierkant tekenen.
De oplossing van het probleem is nu gevonden:
- Je tekent de driehoek met één vierkant er in.
 Van dat vierkant licht één zijde op de lange zijde van de driehoek en één hoekpunt op één van de twee korte zijden.
Van dat vierkant licht één zijde op de lange zijde van de driehoek en één hoekpunt op één van de twee korte zijden.
- Door het "losse hoekpunt" en door punt A teken je een lijn.
- Die lijn snijdt de andere korte zijde.
- Vanuit dat snijpunt teken je het juiste vierkant.
Hoe weet je nu zeker dat dit inderdaad een zuiver vierkant is geworden?
 Nameten kan natuurlijk, maar hele kleine verschillen in de lengtes van de zijden merk je dan nog steeds niet.
Nameten kan natuurlijk, maar hele kleine verschillen in de lengtes van de zijden merk je dan nog steeds niet.Eigenlijk moet je nu een overtuigend bewijs leveren! En dat is nog niet zo eenvoudig. Als je met gelijkvormige driehoeken kunt werken is het echter wel te doen: een uitdaging voor de echte wiskundige.
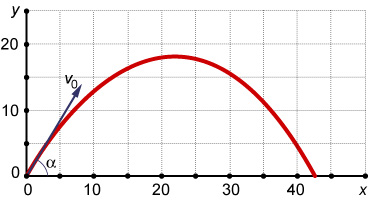
 In diverse takken van sport zie je voorwerpen door de lucht vliegen: vaak een bal of een kogel die een fraaie boog beschrijft.
Deze kogelstoter bijvoorbeeld geeft zijn kogel zo'n kogelbaan.
Wat moet de kogelstoter doen om zijn kogel zo ver mogelijk te werpen?
Is zo hard mogelijk stoten, dus een zo groot mogelijke snelheid meegeven, het belangrijkste? Of is de hoek waaronder hij stoot ook van belang?
In diverse takken van sport zie je voorwerpen door de lucht vliegen: vaak een bal of een kogel die een fraaie boog beschrijft.
Deze kogelstoter bijvoorbeeld geeft zijn kogel zo'n kogelbaan.
Wat moet de kogelstoter doen om zijn kogel zo ver mogelijk te werpen?
Is zo hard mogelijk stoten, dus een zo groot mogelijke snelheid meegeven, het belangrijkste? Of is de hoek waaronder hij stoot ook van belang?