Zelf probleemoplossen

Heb je daarvoor lange stokjes nodig? Van 1 mm lengte of van 1 dm lengte of van 1 m lengte? Of veel langer of korter? Kan er wel een vlieg onderdoor? Reken dat eens na.

• Maak een tekening waaruit blijkt dat die tunnel niet overal even diep onder de grond ligt.
• Bereken hoeveel het diepste punt van de tunnel onder de grond zit.

In een bepaald gezin bestaande uit 2 volwassenen en 2 kinderen is dit al een jarenlange traditie. Elk jaar worden er vier precies gelijke briefjes, met op elk briefje de naam van één gezinslid, op precies dezelfde wijze opgevouwen. Deze lootjes zijn daarom niet van elkaar te onderscheiden. Ze worden bovendien door een zeer betrouwbare buurman in zijn hoge hoed door elkaar geschud, waarop ieder gezinslid met gesloten ogen (en onstuimig kloppend hart) precies één lootje uit de hoed trekt.

Hoe groot is de kans dat er opnieuw moet worden geloot omdat een gezinslid zijn of haar eigen naam aantreft op het briefje dat hij of zij heeft bemachtigd? Geef een uitgebreide toelichting op het antwoord.

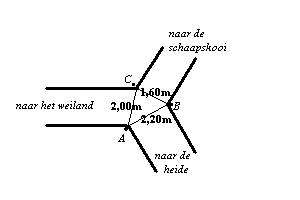
Harmsen heeft bedacht dat het handig is om steeds één van die paden te kunnen afsluiten, dan kunnen zijn schapen gemakkelijk van de éne plaats naar de andere worden gebracht. Hij plaatst daarom na enig nadenken drie hekken op dit kruispunt, één bij A, één bij B en één bij C. Dat doet hij zo, dat hij met twee van die hekken steeds precies één van de wegen kan afsluiten.

Om die hekken te kunnen maken moet hij weten hoe breed elk hek moet worden. Bereken voor boer Harmsen de breedte van elk van die hekken in cm nauwkeurig.

Drie vrienden, A, B en C, gebruiken de maaltijd in een herberg. Ze bestellen na een overvloedig maal dadels als dessert. Voor het dessert komt, vallen ze door overdadig eten en drinken in hun uiterst comfortabele stoelen in slaap. Na een tijdje wordt A wakker en ziet de schaal met dadels staan. Hij nuttigt zijn 1/3 deel en slaapt weer in. Wat later wordt B wakker. Ook hij ziet de schaal met dadels, eet 1/3 deel van de dadels die nog in de schaal liggen op en valt in slaap. Als C tenslotte wakker wordt doet hij hetzelfde en dut weer in. Even later wordt A opnieuw wakker en ziet dat er nog acht dadels op de schaal over zijn gebleven. A begrijpt het probleem en wekt B en C. Samen verdelen ze nu de rest eerlijk over B en C. Hoeveel dadels waren er in totaal voor het dessert?

Je gaat uit van twee even dure auto’s, dus met aanschafkosten houd je voor het vergelijken van beide geen rekening. Hier heb je de gegevens om mee te werken:

Auto op benzine:

• Benzine kost € 1,32 per L (liter)
• Je rijdt gemiddeld 1 op 12, dat is 12 km op 1L benzine
• De jaarlijkse kosten (wegenbelasting, garage, verzekering, etc.) zijn ongeveer € 2400,00

• Dieselolie kost € 1,08 per L (liter)
• Je rijdt gemiddeld 1 op 18, dat is 18 km op 1L diesel
• De jaarlijkse kosten (wegenbelasting, garage, verzekering, etc.) zijn ongeveer € 3800,00

• Hoe groot was de gemiddelde snelheid over de gehele tocht gerekend?
• Leid een formule af voor die gemiddelde snelheid als de gemiddelde snelheid op de heenreis x km/uur en op de terugreis y km/uur was.

Een groep van 100 personen wil een reis maken naar een tentoonstelling in New York. Er wordt een reisbureau ingeschakeld om dat te organiseren. Dat reisbureau chartert een vliegtuig dat maximaal 150 personen kan vervoeren. De reis moet dan € 1000,= p.p. kosten. Het reisbureau geeft bij die prijsopgave aan, dat de reis p.p. goedkoper wordt als ook een deel van overblijvende plaatsen in het vliegtuig kan worden bezet: elke extra deelnemer aan de reis levert een korting op van € 7,= p.p. voor alle passagiers.

• Hoeveel reizigers zal de groep erbij proberen te krijgen? Is dat gunstig voor het reisbureau?
• Bij hoeveel extra passagiers is de totale opbrengst voor het reisbureau zo groot mogelijk?

De gemeente laat een nieuw atletiekveld aanleggen: een rechthoekig binnenterrein met daar omheen de atletiekbaan bestaande uit twee rechte stukken en twee halve cirkels, zie figuur. Een atletiekbaan is 400 m lang.

Hoe groot kan de oppervlakte van het binnenterrein maximaal worden?

De ondernemer wil nu een zo klein mogelijk terrein kopen dat aan al de genoemde voorwaarden voldoet. Welke afmetingen moet dit terrein dan hebben?

Als in een min of meer constante stroom auto’s met ongeveer dezelfde snelheid wordt geremd, kan er file ontstaan. Stel je nu voor dat door werkzaamheden een rijstrook op de snelweg is afgesloten. Bij het invoegen van auto’s naar één rijstrook moet vaak onhandig worden gemanoevreerd, zodat het verkeer moet afremmen of zelfs stil moet staan. Dit is het moment dat een file ontstaat. Zo’n file is niet nodig als iedereen tijdig de juiste doorstroomsnelheid kiest. Daarbij gaat het erom dat zoveel mogelijk auto’s per tijdseenheid de wegversmalling passeren.
Stel een model op voor dit fileprobleem.
Bereken de beste doorstroomsnelheid v in km/h.

Maak gebruik van de volgende aannames (geef ook commentaar op deze aannames):

• Alle auto’s passeren de wegversmalling met dezelfde constante snelheid v.
• Alle auto’s hebben dezelfde lengte L.
• Alle auto’hebben een onderlinge afstand R in m die gelijk is aan de remweg.
• De remweg van alle auto’s is gelijk. Hierbij wordt de volgende vuistregel gehanteerd: "de remweg van een personenauto in meters vind je door de snelheid (in km/h) te delen door 10, de uitkomst te kwadrateren en het resultaat met 0,75 te vermenigvuldigen".