Vierhoeken

Inleiding

Na driehoeken komen vierhoeken...
Vierhoeken zijn al vanaf de Oudheid bestudeerd. Bijzondere vierhoeken hebben namen gekregen als vierkant, rechthoek, parallellogram, ruit, vlieger, trapezium. Ze hebben kenmerkende eigenschappen. Daarover gaat dit onderdeel.

Je leert nu:

• de namen van de meeste bijzondere vierhoeken;
• werken met de eigenschappen van deze bijzondere vierhoeken.

Je kunt al:

• eenvoudige bewijzen leveren, ook uit het ongerijmde;
• werken met congruente en/of gelijkvormige driehoeken bij bewijzen.

Verkennen

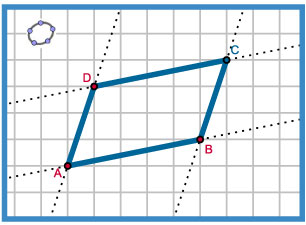
Gebruik de applet in

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Vierhoeken en cirkels > Vierhoeken > Verkennen

Vierhoek ABCD is een parallellogram.

> Wat maakt deze vierhoek een parallellogram? Welke eigenschappen heeft een parallellogram?
> Maak van vierhoek ABCD een vlieger. Welke eigenschappen van een vlieger gebruik je?
> Maak van vierhoek ABCD een rechthoek. Welke eigenschappen van een rechthoek gebruik je?
> Maak van vierhoek ABCD een ruit. Welke eigenschappen van een ruit gebruik je?
> Is elke ruit een vlieger? Is elke vlieger een ruit? Wat zijn de verschillen?
> Maak van vierhoek ABCD een trapezium. Wat is een trapezium precies?
> Maak van vierhoek ABCD een vierkant. Welke eigenschappen van een vierkant gebruik je?

Uitleg

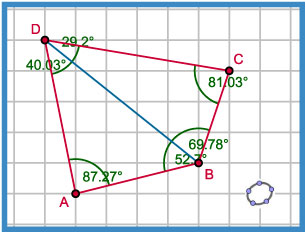
Vierhoek ABCD is een parallellogram. Dat is gemakkelijk gezegd, maar waar herken je dit aan?

Eerst spreek je nauwkeurig af wat een parallellogram is, je geeft een definitie van een parallellogram. Uit die definitie kun je een aantal kenmerkende eigenschappen afleiden, dat worden dan stellingen over parallellogrammen. Die eigenschappen (of de definitie) gebruik je om te herkennen of een vierhoek een parallellogram is.
Welke definitie je gebruikt is vastgelegd op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B.
Daar vind je: "Een parallellogram is een vierhoek met twee paren evenwijdige zijden."
Het parallellogram dat je hier ziet is geconstrueerd vanuit deze definitie: punt C is het snijpunt van twee lijnen die evenwijdig zijn met lijn AB en lijn AD. Maar zijn nu ook de overstaande zijden even groot? En de overstaande hoeken?
Dit zijn eigenschappen die als stelling op de eerder genoemde lijst staan...

‡

Opgaven

1. Bekijk de Uitleg. Bekijk vooral de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B.
   1. Wat is het verschil tussen een definitie en een stelling?
   2. Teken vierhoek `ABCD` met `AB // CD` en `AD // BC`. Teken diagonaal `DB` en toon aan dat `Delta ABD` en `Delta CDB` congruent zijn.
   3. Leg uit dat je nu de stelling hebt bewezen dat de overstaande zijden in een parallellogram even lang zijn.
   4. Bewijs met behulp van congruentie de stelling "Als een vierhoek twee paren even lange overstaande zijden heeft, dan is die vierhoek een parallellogram".


2. Op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B staat de stelling "In een parallellogram zijn de overstaande hoeken even groot".
   Bewijs die stelling met behulp van congruentie.
   


3. Op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B staat de stelling "In een parallellogram delen de diagonalen elkaar middendoor".
   1. Bewijs deze stelling met behulp van congruentie.
   2. Het omgekeerde van deze stelling staat ook in de lijst. Bewijs ook die stelling met behulp van gelijkvormigheid.

Theorie

Er bestaan verschillende soorten vierhoeken. Op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B vind je de volgende definities:

• Een parallellogram is een vierhoek met twee paren evenwijdige zijden.
• Een ruit is een vierhoek met vier even lange zijden.
• Een rechthoek is een vierhoek met vier rechte hoeken.
• Een vierkant is een ruit die tevens rechthoek is.

En dus ontbreekt nog:

• Een vlieger is een vierhoek waarin één van de twee diagonalen de andere loodrecht middendoor deelt.
• Een trapezium is een vierhoek met één paar evenwijdige zijden.

De som van de hoeken van elke vierhoek is 360°. Dit wordt in Voorbeeld 1 bewezen.
Uit de definities van deze soorten vierhoeken kun je m.b.v. stellingen over evenwijdige lijnen en gelijkvormige dan wel congruente driehoeken de eigenschappen afleiden die als stellingen op de genoemde lijst staan vermeld. Zie voorbeelden 2, 3 en 4.

‡

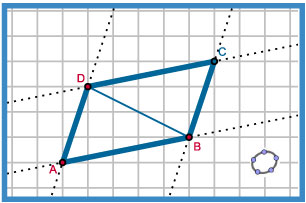
Voorbeeld 1

De som van de hoeken van elke vierhoek is 360°.

Antwoord

Te bewijzen:
In vierhoek ABCD is ∠BAD + ∠ABC + ∠BCD + ∠CDA = 360°.

Bewijs:
Trek diagonaal BD en verdeel de vierhoek zo in twee driehoeken. (Als dit niet mogelijk is, trek je diagonaal AC.) Van elk van deze twee driehoeken is de som van de hoeken 180°. (hoekensom driehoek)
Dus: ∠BAD + ∠ABC + ∠BCD + ∠CDA =
= ∠BAD + ∠ABD + ∠ADB + ∠DBC + ∠BCD + ∠CDB = 180° + 180° = 360°.
Q.e.d.

‡

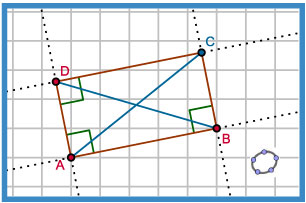
Voorbeeld 2

In een parallellogram zijn de overstaande zijden even lang. (stelling parallellogram)

Antwoord

Te bewijzen:
Als ABCD een parm is, dan |AB| = |CD| en |BC| = |AD|.

Bewijs:
Trek diagonaal BD. Omdat ABCD een parm is zijn de overstaande zijden evenwijdig. En dus: ∠ABD = ∠CDB en ∠ADB = ∠CBD (Z-hoeken).
Omdat |DB| = |BD| is ΔABD congruent met ΔCDB (HZH). En daarom is |AB| = |CD| en |BC| = |AD|.
Q.e.d.

‡

Voorbeeld 3

Als een vierhoek twee paren even lange overstaande zijden heeft, dan is de vierhoek een parallellogram. (stelling parallellogram)

Antwoord

Te bewijzen:
Als |AB| = |CD| en |BC| = |AD|, dan is ABCD een parm.

Bewijs:
Trek diagonaal BD. Omdat in ABCD geldt |AB| = |CD| en |BC| = |AD| en omdat |DB| = |BD| is ΔABD congruent met ΔCDB (ZZZ). En dus: ∠ABD = ∠CDB en ∠ADB = ∠CBD zodat AB//CD en BC//AD (Z-hoeken).
En daarom is ABCD een parm.
Q.e.d.

‡

Voorbeeld 4

In een rechthoek zijn de diagonalen even lang. (stelling rechthoek)

Antwoord

Te bewijzen:
Als ABCD een rechthoek is, dan is |AC| = |BD|.

Bewijs:
Omdat twee loodlijnen op dezelfde rechte lijn evenwijdig zijn (F-hoeken), is een rechthoek ook een parallellogram. En dus zijn de overstaande zijden gelijk. Hieruit kun je (ZZR) gemakkelijk afleiden dat ΔABC en ΔBAD congruent zijn. En daaruit volgt |AC| = |BD|.
Q.e.d.

‡

Opgaven

4. In Voorbeeld 1 wordt aangetoond dat de som van de hoeken van een vierhoek `360`° is.
   1. Teken een vierhoek waarvan ∠`BCD > 180`° is. Waarom kun je nu de vierhoek niet met behulp van diagonaal `BD` in twee driehoeken verdelen?
   2. Pas het bewijs aan voor deze situatie.


5. Bewijs dat de som van de hoeken van een vijfhoek gelijk is aan `540`°.
   


6. In Voorbeeld 2 wordt een stelling bewezen voor een parallellogram die je als eerder hebt bewezen in opgave 2. Bekijk de structuur van het geleverde bewijs.
   1. Bekijk de definitie van een ruit.
   2. Bewijs de stelling: "In een ruit delen de diagonalen de hoeken middendoor."


7. In Voorbeeld 3 wordt een stelling bewezen voor een parallellogram die je als eerder hebt bewezen in opgave 3. Bekijk de structuur van het geleverde bewijs. Bewijs de stelling: "Als in een parallellogram een diagonaal een hoek middendoor deelt, dan is dat parallellogram een ruit."
   


8. In Voorbeeld 4 wordt bewezen dat in een rechthoek de diagonalen even lang zijn. Bewijs dat een parallellogram met even lange diagonalen een rechthoek is.
   


9. Bewijs: "Als in een parallellogram een hoek recht is, dat is dit parallellogram een rechthoek."
   


10. Waarom delen in een vierkant de diagonalen elkaar middendoor en de hoeken elkaar middendoor?
    

Verwerken

11. Een definitie van een vlieger is: "Een vlieger is een vierhoek waarin één van de twee diagonalen de andere loodrecht middendoor deelt".
    1. Bewijs dat hieruit volgt dat in een vlieger minstens twee hoeken even groot zijn.
    2. Bewijs dat hieruit volgt dat een ruit een vlieger is.


12. Beantwoord de volgende vragen eerst "op gevoel". Bewijs dan je antwoord.
    1. Zijn twee rechthoekige driehoeken met dezelfde schuine zijde congruent?
    2. Wanneer zou je twee vierkanten congruent noemen?
    3. Een diagonaal verdeelt een rechthoek in twee driehoeken. Zijn die congruent?
    4. De twee diagonalen verdelen een rechthoek in vier driehoeken. Zijn die alle vier gelijkbenig? Zijn ze twee aan twee congruent?


13. Gebruik de definitie en de stellingen van een rechthoek op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B.
    1. Teken in een rechthoek de diagonalen en geef gelijke hoeken aan.
    2. Bewijs dat de middelloodlijn van een zijde door het snijpunt van de diagonalen en door het midden van de andere zijde gaat.


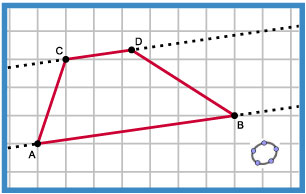14. Een trapezium is een vierhoek waarvan twee overstaande zijden evenwijdig zijn. Dit is een definitie van een trapezium. De twee andere zijden heten dan de opstaande zijden.
    1. Bewijs dat de lijn door de middens van de opstaande zijden van een trapezium evenwijdig is aan de andere twee zijden. (Aanwijzing: trek hulplijnen door die middens.)
    2. Formuleer en bewijs een soortgelijke stelling waarin die middens vervangen zijn door andere punten.
    3. Een trapezium waarvan de opstaande zijden even lang zijn, heet een gelijkbenig trapezium. Bewijs dat een gelijkbenig trapezium twee paren gelijke aanliggende hoeken heeft.
    4. Bewijs dat een trapezium met twee gelijke aanliggende hoeken, een gelijkbenig trapezium is.


15. In een parallellogram `ABCD` is `E` het midden van `AD` en `F` het midden van `BC`. Het lijnstuk `EF` wordt door de diagonaal `AC` gesneden in `S`. Het parallellogram is zo verdeeld in twee driehoeken en twee vierhoeken.
    1. Bewijs dat de driehoeken congruent zijn.
    2. Bewijs dat `|EF| = |AB|`.
    3. Bewijs dat de twee vierhoeken trapezia zijn.

Testen

16. Bewijs: als in een parallellogram de lijn die een hoek middendoor deelt door het tegenoverliggende hoekpunt gaat, is dat parallellogram een ruit.
    


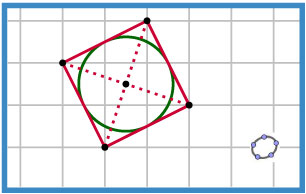17. Een vierkant heeft een ingeschreven cirkel, een cirkel die raakt aan alle zijden.
    1. Toon aan dat een ruit ook een ingeschreven cirkel heeft.
    2. Toon aan dat een parallellogram alleen een ingeschreven cirkel heeft als het een ruit is.