Goniometrische functies differentiëren

Inleiding

Als je met sinusoïden hebt gewerkt, dan weet je dat het hierbij gaat om functies die door transformatie kunnen ontstaan uit de grafiek van y = sin(x) of y = cos(x). Een sinusoïde beschrijft een periodiek verschijnsel. De hellingwaarden van een sinusoïde veranderen daarom ook periodiek.
Niet zo vreemd dus, dat de afgeleide van een sinusoïde ook zelf weer een sinusoïde is.

Je leert nu:

• de afgeleide van een sinusoïde bepalen;
• de differentieerregels toepassen op functies waarin sinus, cosinus of tangens voorkomen.

Je kunt al:

• werken met sinusoïden;
• de differentieerregels gebruiken;
• werken met de afgeleide en de tweede afgeleide, onder andere voor het berekenen van extremen en buigpunten.

Verkennen

Om ook bij goniometrische functies te kunnen werken met hellingen en extremen te kunnen berekenen, moet je de afgeleide van `y = sin(x)` en `y = cos(x)` weten. Je wilt `f(x) = sin(x)` differentiëren.

> Voer in je grafische rekenmachine y1 = sin(x) in. De afgeleide kun je benaderen met y2 = (y1(x + 0,001) – y1(x))/0,001. Breng zowel de functie als de afgeleide in beeld.
> Zou de afgeleide van de sinusfunctie zelf ook een sinusoïde kunnen zijn?
> Welke afgeleide heeft `f(x) = sin(x)`, denk je?
> Bedenk op dezelfde wijze de vermoedelijke afgeleide van `g(x) = cos(x)`.

Uitleg

Het differentiëren van functies waarin sinus en/of cosinus voorkomen is gebaseerd op:

• de afgeleide van `f(x) = sin(x)` is `f'(x) = cos(x)`
• de afgeleide van `f(x) = cos(x)` is `f'(x) = –sin(x)`

Dit heb je bij de opgaven hierboven waarschijnlijk wel vermoed. Maar echt zeker weet je dat pas als je het differentiequotiënt

`(Delta y)/(Delta x) = (sin(x+h) - sin(x))/(h)`

bekijkt voor `h rarr 0`.

Nu kun je met behulp van de formules van Simpson schrijven:
`sin(x + h) - sin(x) = 2 sin(1/2h) * cos(x + 1/2h)`.
Dus:

`(Delta y)/(Delta x) = (sin(x+h) - sin(x))/(h) = (2 sin(1/2h) * cos(x + 1/2h))/h = (sin(1/2h))/(1/2h) * cos(x + 1/2h)`

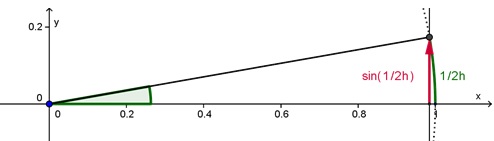
Verder geldt (zie figuur) voor `h rarr 0` dat

• `cos(x + 1/2h) ~~ cos(x)`
• `sin(1/2h) ~~ 1/2h`

Dus als `h rarr 0` geldt `(Delta y)/(Delta x) rarr 1 * cos(x) = cos(x)`

Zo kun je ook de afgeleide van `g(x) = cos(x)` bepalen (dat doe je in opgave 2). En de afgeleide van `h(x) = tan(x) = (sin(x))/(cos(x))` bepaal je met behulp van de quotiëntregel. En zo heb je bij het differentiëren van alle functies waarin sin en cos voorkomen ook de meeste andere differentieerregels weer nodig.

‡

Opgaven

1. Laat zien dat de afgeleide van `g(x) = cos(x)` gelijk is aan `g'(x) = -sin(x)`. Maak daarbij gebruik van `cos(x) = sin(1/2pi - x)` en de kettingregel voor differentiëren.
   


2. De afgeleide van `f(x) = tan(x)` kun je vinden door de quotiëntregel voor differentiëren en de afgeleiden van `y = sin(x)` en `y = cos(x)` te gebruiken. Laat dat zien.
   


3. Met behulp van de al bekende differentieerregels en de regels voor het differentiëren van de drie standaard goniometrische functie die je hierboven hebt afgeleid, kun je alle functies differentiëren. Even oefenen met name bij goniometrsiche functies is nog nuttig. Bereken de afgeleide van de volgende functies.
   1. `f(x) = 2 sin(x)`
   2. `f(x) = sin(2x)`
   3. `f(x) = sin^2(x)`
   4. `f(x) = x^2 sin(x)`
   5. `f(x) = 4 cos(2x) - sin(2x) + 1`
   6. `f(x) = cos^2(x) + 3 cos(x)`
   7. `f(x) = tan(3x)`
   8. `f(x) = sin(x) cos(x)`

Theorie

Het differentiëren van functies waarin sinus en/of cosinus voorkomen is gebaseerd op:

• de afgeleide van f(x) = sin(x) is f'(x) = cos(x)
• de afgeleide van f(x) = cos(x) is f'(x) = –sin(x)

Om de afgeleide van een functie waarin sinus en/of cosinus voorkomen te bepalen heb je ook vaak nog de overige differentieerregels nodig.

Bijvoorbeeld moet je bij afgeleide van een sinusoïde rekening houden met de kettingregel en met de constante-regels. (Zie Voorbeeld 1.)

De afgeleide van f(x) = tan(x) stel je op m.b.v. de quotiëntregel:
f(x) = tan(x) = $\frac{\sin (x)}{\cos (x)}$ geeft
f'(x) = $\frac{\cos (x)\cdot \cos (x)-\sin (x)\cdot -\sin (x)}{{\left(\cos (x)\right)}^2}=\frac{{\cos }^2(x)+{\sin }^2(x)}{{\cos }^2(x)}=\frac{1}{{\cos }^2(x)}$

De afgeleide van f(x) = tan(x) is f'(x) = $\frac{1}{{\cos }^2(x)}$.

‡

Voorbeeld 1

Gegeven is de functie f(x) = –10 + 20 sin(0,1πx – 0,2π) met domein [–10, 10].
Stel m.b.v. differentiëren een vergelijking op van de raaklijn aan de grafiek van f voor x = 0.

Antwoord

f'(x) = 20 cos(0,1πx – 0,2π) · 0,1π = 2π cos(0,1πx – 0,2π).

Daaruit volgt: f'(0) = 2π cos(– 0,2π) ≈ 5,08.
Verder is: f(0) = –10 + 20 sin(– 0,2π) ≈ –21,76.

De vergelijking van de raaklijn wordt: y = 5,08x – 21,76.

‡

Voorbeeld 2

Bij de in- en uitademen varieert het longvolume L (in liters) periodiek met de tijd t (in seconden). Stel je voor dat iemand's longvolume varieert tussen 3,05 en 3,15 L en dat deze persoon 40 keer per minuut in- en uitademt. Neem verder aan dat L(t) een zuivere sinusoïde is.
Op t = 0 is zijn longvolume maximaal. Bereken de grootste snelheid van uitademen.

Antwoord

Dit is een passende formule: L(t) = 3,10 + 0,05 cos($\frac{2\text{π}}{\mathrm{1,5}}$x).
Hierin is t in seconden (er gaan 40 ademhalingen in 60 seconden, dus de periode is 1,5 sec.).

De grootste snelheid van uitademen vindt plaats als de grafiek de evenwichtsstand passeert vanaf een maximum naar een minimum. Bijvoorbeeld op t = 1,5/4 = 0,375.
Die snelheid is dan gelijk aan de afgeleide van L(t) op dat tijdstip.

Nu is: L'(t) = –0,05 sin($\frac{2\text{π}}{\mathrm{1,5}}$x) · $\frac{2\text{π}}{\mathrm{1,5}}$.
En daarom is: L'(0,375) = –0,05 sin($\frac{2\text{π}}{\mathrm{1,5}}$ · 0,375) · $\frac{2\text{π}}{\mathrm{1,5}}$ ≈ –0,021.
De maximale snelheid van uitademen in ongeveer 0,021 L/s.

‡

Voorbeeld 3

Je ziet hier de grafiek van een functie f van de vorm f(x) = sin²(x) – p sin(x). Hierin is p een nog te bepalen onbekende. Het domein van deze functie is [0,2π]. Als p = 1 heeft de grafiek van f vier extremen.
Voor welke waarden van p heeft de grafiek van f vier extremen?

Antwoord

f'(x) = 2 sin(x) cos(x) – p cos(x) = 0 geeft:
cos(x)(2 sin(x) – p) = 0
en dus:
cos(x) = 0   V   sin(x) = 0,5p.

Op [0,2π] heeft cos(x) = 0 twee oplossingen.
Dan moet dit ook gelden voor sin(x) = 0,5p.
Dit betekent –1 < 0,5p < 1 en p ≠ 0.
Dus moet –2 < p < 2 en p ≠ 0.

‡

Opgaven

4. Bekijk Voorbeeld 1. Je ziet daar hoe de vergelijking van de raaklijn aan een sinusoïde wordt opgesteld. Differentieer nu de volgende functies en stel een vergelijking op van de raaklijn voor `x = 0`.
   1. `f(x) = 20 sin(440pi x)`
   2. `f(x) = x cos(x)`
   3. `f(x) = x^2 cos(3x)`
   4. `f(x) = tan^2(1/2 x)`


5. Gegeven de functie `f(x) = sin^2(x) + cos^2(x)`.
   1. Bepaal de afgeleide van deze functie door de afgeleiden van sin en cos te gebruiken.
   2. Met welke formule hangt het resultaat samen?


6. Voorbeeld 2 gaat over iemand's longvolume en de snelheid van in- en uitademen.
   1. Laat zien hoe je de formule voor `V(t)` uit de tekst kunt afleiden.
   2. Leg uit waarom de grootste snelheid van uitademen plaats vindt als de grafiek de evenwichtsstand passeert vanaf een maximum naar een minimum.
   3. Voer nu zelf de berekening van die maximale snelheid van uitademen uit.
   4. En bij welke waarden van `t` krijg je de grootste snelheid van inademen? Hoe groot is die snelheid?


7. Bekijk de familie van functies in Voorbeeld 3.
   1. Neem `p = -1` en bereken alle extremen van deze functie.
   2. Laat zien dat de grafiek van `f` een voor elke `p` een top in `A((pi)/2,f((pi)/2))`heeft.
   3. Er zijn twee waarden van `p`, waarvoor het grootste maximum tweemaal zo groot is als het kleinste maximum. Bereken die waarden van `p`.


8. Gegeven de functie `f(x) = tan(ax)`. Voor welke `a` is de raaklijn aan de grafiek van `f` voor `x=0` evenwijdig met de lijn `2x + y = 6`?
   

Verwerken

9. Differentieer deze goniometrische functies en bereken daarna algebraïsch de eventuele toppen van bijbehorende grafieken.
   1. `f_1(x) = cos^2(x)`
   2. `f_2(x) = 4 sin(2x - 0,25pi) + 10`
   3. `f_3(x) = cos^2(x) + cos(x)`
   4. `f_4(x) = (sin(x))/(1 + cos(x))`


10. Met domein `[0,2pi]` is gegeven de functie `f(x) = sin^2(x) - sqrt3 cos(x) - 1`.
    1. Bereken de exacte extremen van deze functie.
    2. Bereken algebraïsch de buigpunten van deze functie.


11. Met domein `[0,2pi]` is gegeven de functie `f(x) = 1/8 tan(x) - sin(x)`.
    1. Bereken algebraïsch de extremen van deze functie.
    2. Toon aan dat `(0, 0)` een buigpunt van de grafiek is. Stel een vergelijking op van de raaklijn aan de grafiek in dat buigpunt.


12. Op het domein `[0, 2pi]` is gegeven de functie `f(x) = (2 - cos(x))(1 + cos(x))`.
    1. Los exact op: `f(x) = 2`.
    2. Bereken algebraïsch de extremen van `f`.
    3. Voor welke waarden van `p` heeft de vergelijking `f(x) = p` precies twee oplossingen?


13. Het longvolume van een mens kun je registreren met een zogenaamde spirograaf. Bij iemand die hyperventileert geeft de spirograaf de grafiek die je hiernaast ziet.
    1. Hoeveel keer per minuut ademt deze patiënt uit?
    2. Stel een formule op voor het longvolume `V` als functie van de tijd `t` in minuten. Ga ervan uit dat de grafiek een zuivere sinusoïde is.
    3. Benader in twee decimalen nauwkeurig de toenamesnelheid van het longvolume op `t = 7/480`.


14. Gegeven is op het domein `[0, 2pi]` de functie `f` door `f(x) = (sin(x) - cos(x))/(sin(x) + 1)`.
    1. Bereken algebraïsch de nulpunten en de toppen van de grafiek van deze functie.
    2. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in het snijpunt met de `y`-as.
    3. Bepaal in twee decimalen nauwkeurig de lengte van het lijnstuk dat de grafiek van de lijn `y = 1/2` afsnijdt.
    4. De rechte lijn met vergelijking `y = -2x + a` snijdt de grafiek van `f` loodrecht. Bereken a.


15. Gegeven een functie waarvan de grafiek lijkt op een sinusoïde. Alleen de evenwichtsstand is geen horizontale lijn, maar een lijn met helling van `1/2`. Bij deze functie hoort het voorschrift `f(x) = 1/2x + 4 + 2 sin(x)`. Je spreekt nu niet van een evenwichtsstand, maar van een trendlijn.
    1. Welke formule geldt voor de trendlijn? Breng op je grafische rekenmachine zowel de grafiek van `f` als de trendlijn in beeld.
    2. Bereken de toppen van de gegeven functie.
    3. Vallen de `x`-waarden van die toppen samen met die van de toppen van `y = sin(x)`? Geef een verklaring.

Testen

16. Op het domein `[-2pi, 2pi]` is gegeven de functie `f(x) = sin^2(x) + cos(x)`.
    1. Bereken algebraïsch de nulpunten en de toppen van de grafiek van de functie.
    2. Los algebraïsch op: `f(x) > 1`.


17. De kromme `K_f` is de grafiek van de functie `f(x) = x + 2 sin(x)` op het domein `[0, 2pi]`.
    1. Bereken algebraïsch de extremen van `f`.
    2. Stel vergelijkingen op van de rechte lijnen `l` en `m` die `K_f` raken en evenwijdig zijn aan de lijn met vergelijking `y = x`.
    3. `a` is de richtingscoëfficiënt van een raaklijn aan `K_f` . Welke waarden kan `a` aannemen? Licht je antwoord toe.


18. De grafiek van `f(x) = 4 sin((pi x)/10)` op het domein `[0, 10]` heeft precies twee nulpunten `O` en `S` en een top `T`. Door de lijnstukken `OT` en `TS` te trekken ontstaat driehoek `OST`. Punt `A` beweegt over de grafiek van `f` en punt `B` over de lijnstukken `OT` en `TS`. Het lijnstuk `AB` blijft steeds evenwijdig aan de `y`-as.
    Bereken algebraïsch de maximale lengte van `AB` in twee decimalen nauwkeurig.