Sinusoïde als model

Inleiding

Je hebt tot nu toe berekeningen gemaakt en grafieken getekend bij gegeven sinusoïden. Het omgekeerde kan ook: bij een gegeven grafiek van een sinusoïde de formule opstellen. Met die formule kun je snel nieuwe punten van de grafiek vinden.

Verder kun je periodieke verschijnselen waarvan de grafiek golfvormig is, vaak goed benaderen met een sinusoïde. Die sinusoïde is dan een model voor het verschijnsel.

Je leert nu:

bij een getekende sinusoïde de formule opstellen;
sinusoïden gebruiken als model voor een periodiek verschijnsel.

Je kunt al:

de grafiek van een sinusoïde (zowel met sin als cos) tekenen;
de periode, de amplitude, de evenwichtslijn en de horizontale verschuiving van een sinusoïde aflezen uit de formule, dan wel uit de grafiek.

Verkennen

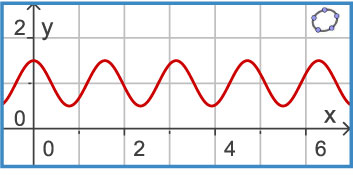
Je ziet hier een sinusoïde.
Toppen zijn onder andere (0; 1,5), ( $\frac{1}{4} π$ ; 0,5) en ( $\frac{1}{2} π$ ; 1,5).
Het domein is $ℝ$ .

> Bepaal de periode, de amplitude en de evenwichtslijn.
> Stel een passende formule op, uitgaande van de sinus.
> Stel een passende formule op, uitgaande van de cosinus.

Uitleg

Bekijk de getijdeninformatie van Harlingen.
Je ziet dat bij hoogwater de waterstand h ongeveer 80 cm boven NAP en dat bij laagwater de waterstand ongeveer 100 cm onder NAP zit. Verder liggen de opeenvolgende tijdstippen van hoogwater (net als die van laagwater) ongeveer 12 uur en 15 minuten uit elkaar. Dat betekent een periode van 12,25 uur. Op zekere dag is het hoogwater om 6:00 uur. Hier zie je een schets van een bijpassende grafiek.

De periode is 12,25 uur, dus b = $\frac{2 π}{12,25}$ ≈ 0,52.
De waterstand ligt tussen 0,8 m en –1,0 m, dus de amplitude is a = 0,9 m.
De evenwichtslijn ligt 0,9 m onder hoogwater en daarom is d = –0,1.
Hoogwater moet bij t = 6 zitten, het direct ervoor liggende punt op de evenwichtslijn zit daar een kwart periode voor, dus bij t = 6 – 3,0625 ≈ 2,94. Dit betekent dat c ≈ –2,94.

De bijpassende sinusoïde wordt: h(t) ≈ 0,9 sin(0,52(t – 2,94)) – 0,1.

‡

Opgaven

Bekijk hoe bij de Uitleg een sinusoïde wordt opgesteld als model voor de waterstand bij Harlingen.
1. Leg uit hoe uit de gegevens de periode, de amplitudo en de evenwichtslijn wordt gevonden.
2. Stel een bijpassende formule op uitgaande van `y = cos(x)`.
3. Laat zien dat beide formules dezelfde grafiek opleveren. Maak die grafieken op je grafische rekenmachine.

Ga uit van de functie `y = sin(x)`. Schrijf het voorschrift op van de periodieke functies die ontstaan bij de volgenden wijzigingen:
1. De amplitude wordt 4.
2. De amplitude wordt 10 en de evenwichtsstand wordt 20.
3. De periode wordt `4pi` en de amplitude wordt 4.
4. De horizontale verschuiving is 2, de periode wordt 10, de amplitude wordt 5 en de evenwichtsstand wordt 10.

Theorie

Wanneer je een periodiek verschijnsel kunt beschrijven met een sinusoïde kun je daarbij een passend functievoorschrift maken door

de evenwichtslijn y = d te bepalen;
de amplitude a (maximale uitwijking van de evenwichtslijn) te bepalen;
de periode p te bepalen;
de horizontale verschuiving (t.o.v. de standaardgrafiek) c te bepalen.

Er zijn dan twee functievoorschriften mogelijk:

f(x) = a sin(b(x – c₁) + d waarin b = $\frac{2 π}{p}$
f(x) = a cos(b(x – c₂) + d waarin b = $\frac{2 π}{p}$

Let er wel op dat de waarden voor a, b en d bij beide grafieken hetzelfde zijn, maar de waarden van c niet. De verschuiving t.o.v. de standaardsinus is immers anders dan t.o.v. de standaardcosinus.

‡

Voorbeeld 1

Deze sinusoïde staat bij de theorie.
Welk functievoorschrift kun je er bij maken uitgaande van de standaardsinus? En welk functievoorschrift uitgaande van de standaardcosinus?

Antwoord

De maxima van de functie zijn 300 en de minima 50. Dus:

de amplitude is a = $\frac{300 - 50}{2}$ = 125;
de evenwichtslijn is y = 300 – 125 = 175;

Twee opvolgende maxima zitten bij x = 3 en x = 11, dus de periode is p = 8.

Ga je nu uit van de standaardsinus, dan is de horizontale verschuiving de x-waarde van een punt op de grafiek op de evenwichtslijn op het moment dat de grafiek daar stijgt. Hier dus x = 1.
Het functievoorschrift wordt dan: f(x) = 125 sin( $\frac{2 π}{8}$ (x – 1)) + 175.

Ga je uit van de standaardcosinus, dan is de horizontale verschuiving de x-waarde van een punt op de grafiek waar een maximum zit. Hier dus bijvoorbeeld x = 3.
Het functievoorschrift wordt dan: f(x) = 125 cos( $\frac{2 π}{8}$ (x – 3)) + 175.

‡

Voorbeeld 2

Een sinusoïde heeft een maximum van 1 en een minimum van –5.
Het domein is $ℝ$ .
De evenwichtswaarde 2 wordt onder andere bereikt als x = $\frac{5}{3} π$ en daarna als x = $\frac{11}{3} π$ .
Tussen deze beide x-waarden ligt de grafiek boven de evenwichtslijn.

Stel een formule op voor de beschreven sinusoïde.

Antwoord

De formule krijgt bijvoorbeeld de vorm y = a sin(b(x – c)) + d of de vorm y = a cos(b(x – c)) + d.

De twee punten op de evenwichtslijn liggen een halve periode uit elkaar.

De periode is dus 2 · ( $\frac{11}{3} π$ – $\frac{5}{3} π$ ) = 4π, dus b = $\frac{2 π}{4 π} = \frac{1}{2}$ .
De evenwichtslijn is y = –2.
De amplitude a is 3.

Omdat je weet waar de punten op de evenwichtslijn zitten, kun je het gemakkelijkst uitgaan van de standaardsinus. De horizontale verschuiving is dan $\frac{5}{3} π$ , want bij die x-waarde hoort een punt op de evenwichtslijn waarin de grafiek omhoog gaat.

De gevraagde formule is: y = 3 sin( $\frac{1}{2}$ (x – $\frac{5}{3} π$ ) – 2.

‡

Voorbeeld 3

Als je een cilinder met een diameter van 4 cm schuin doorsnijdt en vervolgens openknipt en plat neerlegt, kun je deze figuur krijgen. De bovenrand is een zuivere sinusoïde.

Stel voor deze rand een formule op. Neem aan dat punt P de coördinaten (0,0) heeft.

Antwoord

Je ziet hoe je dan de assen kiest.
Vervolgens bepaal je:

de evenwichtslijn y = 2;
de amplitude is 2;
de periode is 4π.

Het maximum zit halverwege de bovenrand bij x = 2π.
Het gemakkelijkst is nu een formule met cosinus, dan is de horizontale verschuiving 2π.

De formule wordt: y = 2 cos(0,5(x – 2π)) + 2 met domein [0, 4π].

‡

Opgaven

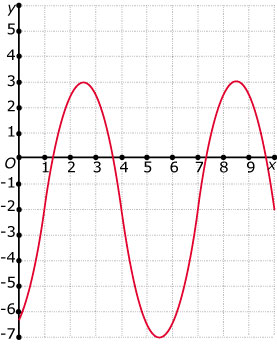Je ziet hier een sinusoïde getekend. Maak er een functievoorschrift bij, uitgaande van `y = sin(x)`.
Bekijk eventueel eerst Voorbeeld 1.

Maak bij de sinusoïde van de vorige opgave een functievoorschrift uitgaande van `y = cos(x)`.

De grafiek van een sinusoïde `f` heeft minimum 10 voor `x = 1` en eerstvolgend maximum 26 voor `x = 13`.
1. Bereken de periode, de evenwichtslijn en de amplitude. Bekijk eventueel eerst Voorbeeld 2.
2. Geef een passende formule, gebruik naar keuze de sinus of de cosinus.
3. Bereken in twee decimalen nauwkeurig: `f(12)`, `f(12,25)`, `f(12,5)`, `f(12,75)` en `f(13)`.
4. Los op: `f(x) > 16`.

Bestudeer Voorbeeld 3.
1. Stel voor de bovenrand een formule op uitgaande van `y = sin(x)`.
2. Een lijn evenwijdig aan `PQ` snijdt de bovenrand in `A` en `B`. Gegeven is `AB = 4` cm. Bepaal de coördinaten van `A` en `B`.

Verwerken

Stel bij deze vier sinusoïden een passend functievoorschrift op.

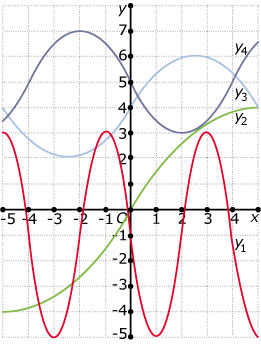
Bij de vorige opgave zijn bij elke sinusoïde meerdere functievoorschriften mogelijk.
1. Geef er bij `y_1` minstens drie.
2. Gebruik één van deze functievoorschriften om op te lossen: `y_1 = -2`. Geef benaderingen in drie decimalen nauwkeurig.

De grafiek van `f` is sinusvormig. De evenwichtslijn is `y = 1`, de amplitude is 2, de periode is `pi` en de grafiek gaat stijgend door het punt `(1/6 pi, 1)`.
1. Stel een formule op voor `f(x)`.
2. Bereken met die formule `f(0)`.
3. Los op: `f(x) <= 0`.

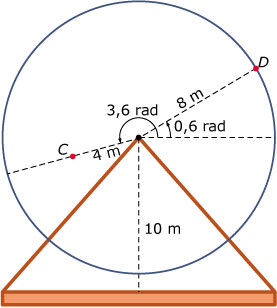Een reuzenrad bevat de stoeltjes `C` en `D`. Stoeltje `C` draait op een afstand van 4 meter van de as in de rondte, stoeltje `D` op een afstand van 8 meter. De as van het reuzenrad bevindt zich op 10 meter boven de grond. Bekijk de getekende situatie. Het reuzenrad draait in 8 seconden één keer rond. Op `t = 0` staat stoeltje `D` zo hoog mogelijk. Het reuzenrad draait tegen de wijzers van de klok in.
1. Bereken bij elke stand de hoogte van de stoeltjes `C` en `D` ten opzichte van de grond.
2. Stel een passend functievoorschrift op voor de hoogte van stoeltje `D`.
3. Hoe hoog staat stoeltje `C` op tijdstip `t = 1413,25`?
4. Hoe lang zit je in stoeltje `C` elk rondje hoger dan 12 m?

Testen

Functie `f` met voorschrift `f(x)` heeft een sinusvormige grafiek met een minimum in het punt `(20,300)` en een eerstvolgend maximum in het punt `(32,400)`.
1. Maak een schets van deze grafiek met `x` van `0` tot ten minste `40`.
2. Bereken de periode, de amplitude en de evenwichtslijn en stel een passend functievoorschrift op.
3. Bereken `f(50)`, `f(51)` en `f(52)`.
4. Los op: `f(x) = 325`.

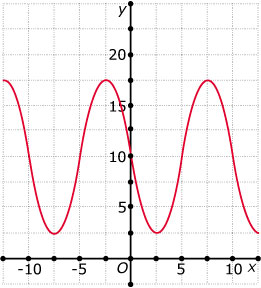Stel bij deze sinusoïde twee passende functievoorschriften op.

Onze ademhaling is bij benadering een periodiek verschijnsel. Een gezonde volwassen man ademt ongeveer 12 keer per minuut in en weer uit. De longinhoud `V(t)` kan daarbij met zo’n halve liter toe- of afnemen, waarin `t` de tijd in seconden is. Het longvolume na inademen is 5,2 liter.
1. Hoe groot is de ademhalingsfrequentie per minuut?
2. Ga ervan uit dat `V(t)` een sinusoïde is met op `t = 0` een maximale longinhoud. Teken de grafiek van de longinhoud `V` uitgezet tegen de tijd `t`.
3. Stel bij deze situatie een formule op voor `V(t)`.