
Sinusoïde als model
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Uitleg
Lees eerst de Uitleg goed door.
Opgaven
-
Bekijk hoe bij de Uitleg een sinusoïde wordt opgesteld als model voor de waterstand bij Harlingen.
-
Leg uit hoe uit de gegevens de periode, de amplitudo en de evenwichtslijn wordt gevonden.
-
Stel een bijpassende formule op uitgaande van `y = cos(x)`.
-
Laat zien dat beide formules dezelfde grafiek opleveren. Maak die grafieken op je grafische rekenmachine.
-
Ga uit van de functie `y = sin(x)`. Schrijf het voorschrift op van de periodieke functies
die ontstaan bij de volgenden wijzigingen:
- De amplitude wordt 4.
- De amplitude wordt 10 en de evenwichtsstand wordt 20.
- De periode wordt `4pi` en de amplitude wordt 4.
- De horizontale verschuiving is 2, de periode wordt 10, de amplitude wordt 5 en de evenwichtsstand wordt 10.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
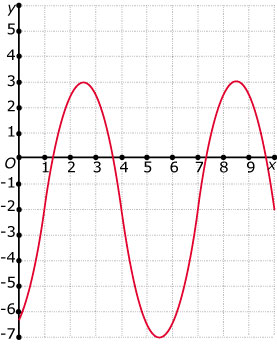 Je ziet hier een sinusoïde getekend.
Maak er een functievoorschrift bij, uitgaande
van `y = sin(x)`.
Je ziet hier een sinusoïde getekend.
Maak er een functievoorschrift bij, uitgaande
van `y = sin(x)`.
Bekijk eventueel eerst Voorbeeld 1.
-
Maak bij de sinusoïde van de vorige opgave een functievoorschrift uitgaande van `y = cos(x)`.
-
De grafiek van een sinusoïde `f` heeft minimum 10 voor `x = 1` en eerstvolgend maximum 26 voor `x = 13`.
-
Bereken de periode, de evenwichtslijn en de amplitude. Bekijk eventueel eerst Voorbeeld 2.
-
Geef een passende formule, gebruik naar keuze de sinus of de cosinus.
-
Bereken in twee decimalen nauwkeurig: `f(12)`, `f(12,25)`, `f(12,5)`, `f(12,75)` en `f(13)`.
-
Los op: `f(x) > 16`.
-
Bestudeer Voorbeeld 3.
-
Stel voor de bovenrand een formule op uitgaande van `y = sin(x)`.
-
Een lijn evenwijdig aan `PQ` snijdt de bovenrand in `A` en `B`. Gegeven is `AB = 4` cm. Bepaal de coördinaten van `A` en `B`.
Verwerken
-
Stel bij deze vier sinusoïden een passend functievoorschrift op.
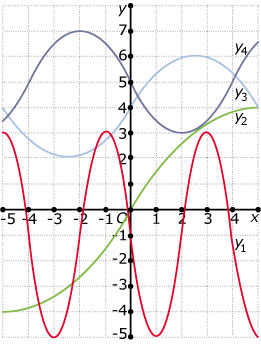
-
Bij de vorige opgave zijn bij elke sinusoïde meerdere functievoorschriften mogelijk.
-
Geef er bij `y_1` minstens drie.
-
Gebruik één van deze functievoorschriften om op te lossen: `y_1 = -2`. Geef benaderingen in drie decimalen nauwkeurig.
-
De grafiek van `f` is sinusvormig. De evenwichtslijn is `y = 1`, de amplitude is 2, de periode is `pi` en de grafiek gaat stijgend door het punt `(1/6 pi, 1)`.
- Stel een formule op voor `f(x)`.
- Bereken met die formule `f(0)`.
- Los op: `f(x) <= 0`.
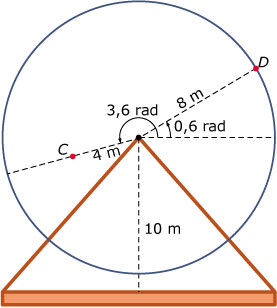 Een reuzenrad bevat de stoeltjes `C` en `D`. Stoeltje `C` draait op een afstand van 4 meter van de as in de rondte, stoeltje `D` op een afstand van 8 meter.
De as van het reuzenrad bevindt zich op 10 meter boven de grond. Bekijk de getekende situatie. Het reuzenrad draait in 8 seconden één keer rond.
Op `t = 0` staat stoeltje `D` zo hoog mogelijk. Het reuzenrad draait tegen de wijzers van de klok in.
Een reuzenrad bevat de stoeltjes `C` en `D`. Stoeltje `C` draait op een afstand van 4 meter van de as in de rondte, stoeltje `D` op een afstand van 8 meter.
De as van het reuzenrad bevindt zich op 10 meter boven de grond. Bekijk de getekende situatie. Het reuzenrad draait in 8 seconden één keer rond.
Op `t = 0` staat stoeltje `D` zo hoog mogelijk. Het reuzenrad draait tegen de wijzers van de klok in.
- Bereken bij elke stand de hoogte van de stoeltjes `C` en `D` ten opzichte van de grond.
- Stel een passend functievoorschrift op voor de hoogte van stoeltje `D`.
- Hoe hoog staat stoeltje `C` op tijdstip `t = 1413,25`?
- Hoe lang zit je in stoeltje `C` elk rondje hoger dan 12 m?
Testen
-
Functie `f` met voorschrift `f(x)` heeft een sinusvormige grafiek met een minimum in het punt `(20,300)` en een eerstvolgend maximum in het punt `(32,400)`.
-
Maak een schets van deze grafiek met `x` van `0` tot ten minste `40`.
-
Bereken de periode, de amplitude en de evenwichtslijn en stel een passend functievoorschrift op.
-
Bereken `f(50)`, `f(51)` en `f(52)`.
- Los op: `f(x) = 325`.
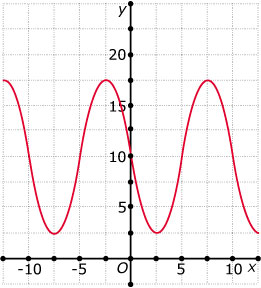 Stel bij deze sinusoïde twee passende functievoorschriften op.
Stel bij deze sinusoïde twee passende functievoorschriften op.
-
Onze ademhaling is bij benadering een periodiek verschijnsel. Een gezonde volwassen man ademt ongeveer 12 keer per minuut in en weer uit.
De longinhoud `V(t)` kan daarbij met zo’n halve liter toe- of afnemen, waarin `t` de tijd in seconden is. Het longvolume na inademen is 5,2 liter.
-
Hoe groot is de ademhalingsfrequentie per minuut?
-
Ga ervan uit dat `V(t)` een sinusoïde is met op `t = 0` een maximale longinhoud. Teken de grafiek van de longinhoud `V` uitgezet tegen de tijd `t`.
-
Stel bij deze situatie een formule op voor `V(t)`.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodieke modellen > Theorie Je ziet hier een sinusoïde getekend.
Maak er een functievoorschrift bij, uitgaande
van `y = sin(x)`.
Je ziet hier een sinusoïde getekend.
Maak er een functievoorschrift bij, uitgaande
van `y = sin(x)`.
 Een reuzenrad bevat de stoeltjes `C` en `D`. Stoeltje `C` draait op een afstand van 4 meter van de as in de rondte, stoeltje `D` op een afstand van 8 meter.
De as van het reuzenrad bevindt zich op 10 meter boven de grond. Bekijk de getekende situatie. Het reuzenrad draait in 8 seconden één keer rond.
Op `t = 0` staat stoeltje `D` zo hoog mogelijk. Het reuzenrad draait tegen de wijzers van de klok in.
Een reuzenrad bevat de stoeltjes `C` en `D`. Stoeltje `C` draait op een afstand van 4 meter van de as in de rondte, stoeltje `D` op een afstand van 8 meter.
De as van het reuzenrad bevindt zich op 10 meter boven de grond. Bekijk de getekende situatie. Het reuzenrad draait in 8 seconden één keer rond.
Op `t = 0` staat stoeltje `D` zo hoog mogelijk. Het reuzenrad draait tegen de wijzers van de klok in.
 Stel bij deze sinusoïde twee passende functievoorschriften op.
Stel bij deze sinusoïde twee passende functievoorschriften op.